† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61471007, 61531002, 61522101, and 11275206) and the Seeding Grant for Medicine and Information Science of Peking University, China (Grant No. 2014-MI-01).
Dynamics of the axial mode transition process in a 0.33-THz second-harmonic gyrotron is investigated to reveal the physical mechanism of realizing broadband frequency tuning in an open cavity circuit. A new interaction mechanism about propagating waves, featured by wave competition and wave cooperation, is presented and provides a new insight into the beam-wave interaction. The two different features revealed in the two different operation regions of low-order axial modes (LOAMs) and high-order axial modes (HOAMs) respectively determine the characteristic of the overall performance of the device essentially. The device performance is obtained by the simulation based on the time-domain nonlinear theory and shows that using a 12-kV/150-mA electron beam and TE−3,4 mode, the second harmonic gyrotron can generate terahertz radiations with frequency-tuning ranges of about 0.85 GHz and 0.60 GHz via magnetic field and beam voltage tuning, respectively. Additionally, some non-stationary phenomena in the mode startup process are also analyzed. The investigation in this paper presents guidance for future developing high-performance frequency-tunable gyrotrons toward terahertz applications.
Terahertz (THz) wave has attracted extensive attention in many scientific applications including detection, communication, biomedicine, imaging, and spectroscopy.[1–7] One of the important applications that have been continuously accelerating the development of the THz gyrotron is sensitivity-enhanced nuclear magnetic resonance (NMR) via dynamic nuclear polarization (DNP).[5,7] The required level of the output power and the needed specific spectral characteristics make the gyrotron oscillator a most promising and high-performance device for such an application. The gyrotron is a fast-wave vacuum electron device based on the mechanism of electron cyclotron maser (ECM) and can operate with an over-mode open cavity, which permits a considerably higher output power level than the semiconductor device and other competing THz vacuum sources, such as the extended interaction oscillator (EIO), the extended interaction klystron (EIK) and the backward-wave oscillator (BWO).[6] Compared with the free electronic laser (FEL), the gyrotron also has the advantage in compact size.
The operating frequency of a gyrotron is close to the electron cyclotron frequency, ωc = eB0/γm0, where B0 is magnetic field and γ is relativistic factor, e and m0 are electron charge and mass, respectively. For a gyrotron operating at the sth cyclotron harmonic, its operating frequency can be estimated to be f = 28sB0/γ. So one can see that a very strong magnetic field is required when the gyrotron operates at THz band in the fundamental mode, but the magnetic field can be significantly reduced when the gyrotron operates at a harmonic of electron cyclotron resonance.[6,8,9] Though quite a lot of relevant researches have been carried out,[10–16] the dynamics of axial mode behavior which plays an important role in determining the performance of tunable gyrotrons, is still rarely studied.
A traditional gyrotron, such as the gyrotron used in the fusion plasma heating, usually adopts an interaction circuit, which operates in the fundamental axial mode with a high quality factor and radiates almost at a single frequency. However, the gyrotron for DNP-NMR application needs a reasonable tunable bandwidth to well achieve the synchronization between the THz wave and the NMR polarization system. The successful solution to realize frequency tunable gyrotron is to tune the system parameters to force the system to transit between different axial modes with comparatively low quality factors in the open-cavity interaction circuit. Hence, systematic studies of dynamics of the axial mode transition in open cavity are very important to promote the development of the frequency tunable THz gyrotron.
Many previous studies of mode startup process have assumed a fixed field profile,[17–20] but this assumption is not well fulfilled in DNP-NMR gyrotron which operates based on axial mode transition. Hence, the non-fixed field time-dependent code based on the time-domain nonlinear theory is developed and used to study the performance of the 0.33-THz gyrotron oscillator which operates at the second-harmonic cyclotron and low voltages. Then a new interaction mechanism about propagating waves, featured by wave competition and wave cooperation, is presented and provides a new insight into the beam-wave interaction to study the dynamic axial mode behavior. What is more, some non-stationary phenomena in the mode startup process which cannot be observed under the fixed field assumption are found and analyzed.
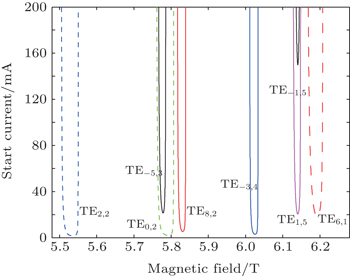
The counter-rotating TE−3,4 cylindrical waveguide mode is selected as an operating mode because this mode can provides strong coupling with the beam among second-harmonic modes while the guiding center of electron beam is far enough from the center of cavity. The points of highest intensity (the first Bessel function maxima) of the mode pattern are away from the cavity walls, thereby avoiding the high ohmic heating encountered with the whispering gallery modes (m ≫ n for mode TEm,n) and the mode competition with high-order TE0,n modes. Moreover, this mode is comparatively isolated from other surrounding competing modes in the beam-wave interaction spectrum.
The excitation frequency of a gyrotron is determined by the frequency of eigenmode in the interaction cavity. It is always close to the cutoff frequency fm,n of the cavity. For the TE modes in the vacuum cylindrical waveguide, the cutoff frequency is
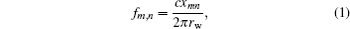
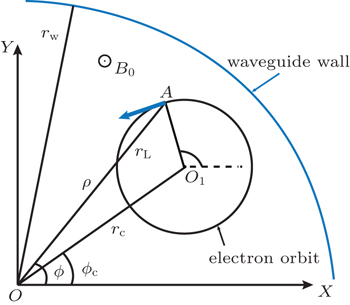
For operation at 0.33 THz in the mode TE−3,4, the cavity radius (radius of the straight section) is chosen to be 2.109 mm. The geometry of the gyrotron circuit is shown in Fig.
The guiding center radius of electron beam rc is selected to be 0.93 mm, where the first maximum of Bessel function Jm+n(x) is located, to obtain favorable coupling to the operating mode. The coupling factor Cm,n between electron beam and operating mode is given by[23]

Cold cavity simulation allows one to determine cavity parameters efficiently, such as the resonant frequency of the cavity eigenmodes, axial field profile and quality factor Q, which can be conducible to the cavity design. The characteristic of the cold cavity is analyzed based on the weakly irregular waveguide theory.[24] In the cold cavity without electron beam, a series of resonant axial modes exist which can be specified by their resonant frequencies and axial profiles. The simulation results give the values of resonant frequency and the diffractive quality factor Qd of operation mode TE−3,4,q ranging from q = 1 to q = 7, which are listed in Table
| Table 1. Frequencies and diffractive quality factors for the TE−3,4,q modes. . |
Mode competition can be studied based on the starting current preliminarily. The starting current is the threshold to be overcome to excite a given wave guide mode and can be calculated from the linear theory of the gyrotron oscillator.[21,23,26,27] Based on the cold cavity analysis above, starting currents for the operating and neighboring modes are shown in Fig.
For analyzing the beam-wave interaction, time-domain self-consistent calculations are employed by using the following theoretical model. A thin annular electron beam is located at the rc radius (as shown in Fig.
The transverse electric field of the mode is expressed as

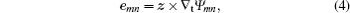

According to the well-known Maxwell equations, we neglect the space charge effect and obtain the wave equation
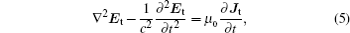
Neglecting the beam effects on the transverse mode profile, we operate on both sides of Eq. (

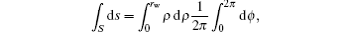

The transverse alternating beam current density
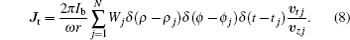
Here Ib is the beam current, Wj is a normalized weighting factor for the j-th electron,
Substitute Eq. (

The phase factor is Λj = − ωtj + (m − s)ϕc + sθj, and the radiation boundary conditions[28] are

The electron beam is represented as an ensemble of particles in the form of function (

Here
The beam-wave interaction theory consists of the system of Eqs. (
In Fig.
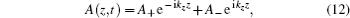
Figure
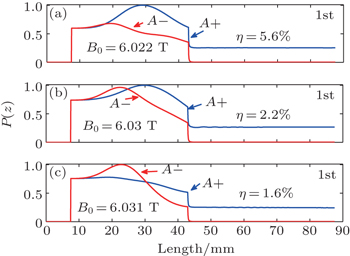 | Fig. 5. Normalized power profiles of the first axial mode under different magnetic fields: (a) B0 = 6.022 T, (b) B0 = 6.03 T, and (c) B0 = 6.031 T. |
Under a higher magnetic field B0 = 6.031 T in Fig.
Furthermore, it is interesting that under the magnetic field B0 = 6.047 T in Fig.
 | Fig. 6. Normalized power profiles of the axial modes from q = 1 to q = 3 under different magnetic fields: (a) B0 = 6.022 T, (b) B0 = 6.038 T, and (c) B0 = 6.047 T. |
In the time-dependent simulation some non-stationary phenomena are observed. Under the magnetic field 6.038 T where a LOAM operates, non-stationary oscillation is observed at a saturation amplitude level. As shown in Fig.
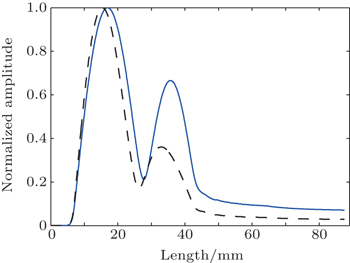 | Fig. 8. Profiles of normalized filed versus length at 27 ns (blue solid line) and 32.5 ns (black dashed line). |
Unlike the startup scenarios in Fig.
The output efficiency and frequency tuning range via magnetic field and beam voltage tuning are shown in Figs.
 | Fig. 11. Self-consistent simulations of efficiency and frequency tuning as a function of magnetic field. |
Generally speaking, a compromise between the smooth efficiency output and the tuning bandwidth determines the overall performance of the device, which leads to a finite-bandwidth. The HOAMs have lower quality factors than the LOAMs and exhibit weaker coupling with the electron beam. Utilizing a long cavity or increasing the beam current makes the HOAMs excitation easier to provide wider frequency tuning bandwidth, but the problem of mode competition from both axial modes and transverse modes can be critical. In our investigation, the long cavity increases the Q factors of HOAMs and enhances the wave feedback. But on the other hand, the high Q factor leads to a large Q factor separation (Q-separation) between neighboring axial modes, and the Q-separation between the q-th axial mode and (q + 1)-th axial mode can be estimated as (2q + 1)Q1/q2(q + 1)2, where Q1 refers to the Q factor of the fundamental axial mode. The large Q-separation produces a negative effect on the transition process between neighboring axial modes and results in an axial-mode competition. As shown in Fig.
In this paper, the non-fixed field time-dependent code is developed and used to investigate the output performance of the second harmonic gyrotron oscillator. A frequency tuning range of 0.85 GHz with an efficiency range of 0.12%–15% is achieved by tuning magnetic field. By tuning voltage, a frequency tuning range of 0.6 GHz with an efficiency range of 0.14%–12% is achieved. Both efficiency spectra exhibit obvious fluctuations in the HAOMs area with an average efficiency of about 2%. The characteristics of the axial mode transition are analyzed, and some new non-stationary phenomena in the mode startup process which cannot be observed under the fixed field assumption are found.
Results show that the transition from forward wave interaction to backward wave interaction happens with magnetic field increasing. Fundamental axial mode interaction can provide higher peak output efficiency but the two-wave competition leads to the rapid decline in output efficiency with magnetic field increasing. The interaction in the HOAM area behaves as two-wave cooperation and can provide better frequency tunability with comparatively low efficiency. What is more, mode competition between the first and second axial mode is found under the low magnetic field and this is considered as another reason for the decline in output efficiency. The problems from both axial modes and transverse modes should always be notable, and the mode competition should be avoided to achieve stable operation. Generally speaking, the compromise between the stable, smooth output and the tuning bandwidth determines the overall performance of the device.
The present work should be beneficial to the gyrotron used in DNP-NMR and other terahertz applications, in which the gyrotron needs a reasonable tunable bandwidth and operates based on axial modes transition.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 |