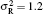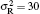Along with the rapid development of terahertz (THz) sources and detectors, recent advances in THz wave technologies have attracted more and more attention due to the huge bandwidth, large capacity, and its enormous potential for applications on wireless communications. The higher carrier frequency and broader bandwidth of THz band can contain more information, and unallocated spectrum resources can avoid much interference, congestion, which are competitive advantages for ultra-high speed data transmission in comparison with microwave and millimeter communications.^[1,2] However, atmospheric absorption, scattering, and scintillation will limit the THz communication transmission distance and data rate. THz beams are sensitive to the properties of the medium and will be influenced inevitably by atmospheric turbulence when propagating through the atmosphere near the ground.^[3,4] The path loss and atmospheric scintillation will seriously deteriorate the signal-to-noise ratio (SNR) and degrade the bit-error-rate (BER) performance of THz wireless communication links. Scintillation theory has been proposed in many practical light propagation applications and the atmospheric turbulence is in accordance with the scintillation index.^[5] Error control coding technology can be an efficient solution to improve the system performance in similar channels.^[6,7]

Low density parity check (LDPC) codes^[8] are considered to be one of the most efficient forward error correction (FEC) schemes because of their excellent performance approaching Shannon’s limit^[9] and significant low decoding complexity when decoded with the belief-propagation (BP) algorithm or sum-product algorithm (SPA).^[10] Applications of LDPC codes on optical communications have been investigated in various methods and exhibit great advantages against channel fading.^[11–13] However, to the best of our knowledge, there have been few papers reported about the THz channel coding technology so far. Consequently, it is obligated to apply some powerful channel coding schemes to ensure the THz wireless link quality and LDPC codes are good candidates.

In this paper, we propose an LDPC code scheme to improve the BER performance of an on-off keying (OOK) modulated THz wireless communication system based on quantum-cascade laser (QCL) as the transmitter and quantum-well photodetector (QWP) as the receiver^[14,15] and verified the feasibility of the scheme. The paper is structured as follows. In Section 2, the THz wave propagation characteristics in atmosphere are analyzed and the related communication channel model is set up. Then LDPC decoder design is introduced in Section 3. In Section 4, numerical simulations of LDPC codes with soft decision decoding algorithm in different atmospherical conditions, propagation distance, and bit rate are carried out. Simulation results demonstrate the great performance of LDPC codes in future ultra-high speed THz wireless communications. Concluding remarks wrap up this paper in Section 5.

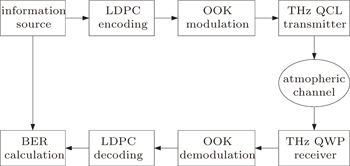
A point-to-point THz wireless communication system using intensity modulation and direct detection (IM/DD) with OOK modulation was observed^[15] and its simplified block diagram is shown in Fig. 1. The laser beams propagate along a horizontal path through a turbulence channel with additive white Gaussian noise (AWGN). The channel is assumed to be memoryless, stationary, and ergodic, with independent and identically distributed intensity fading statistics. The instantaneous received signal y_k can be described by the conventional channel model^[16]

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Atmospheric terahertz communication block scheme.

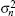
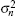
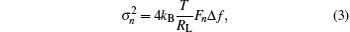
The QWP receiver noise is caused by shot noise, thermal noise and dark current. It is assumed that dark current and shot noise is negligible because thermal noise is dominated in the total noise, so the noise variance can be expressed as

Channel characteristics at THz (0.06 THz∼1 THz) band communication has been fully studied in recent years.^[17,18] In the contrary, there is no enough theory about THz wireless channel characteristics beyond 1 THz due to lack of related experimental measurements. The THz signal transmission through atmospheric channel is inevitably disrupted by atmospheric turbulence, attenuation, and geometric loss. Several statistical models have been reported to estimate the atmospheric turbulence effects,^[19] and gamma–gamma distribution has been accepted as the most suitable model for a wider range of turbulence conditions from weak to strong in various communication systems.^[20] According to the gamma–gamma model, the probability density function (PDF) of the received optical irradiance can be given by^[19,20]

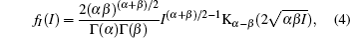
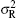
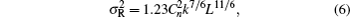
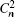
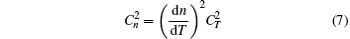
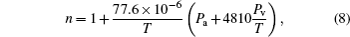
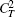
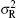
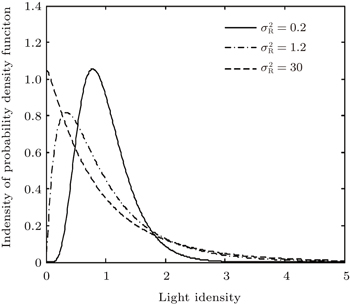To simplify the discussion, is generally used as a metric of turbulence strength which is combination of propagation distance, wave length and the parameter . The evolution of the gamma-gamma models in Eq. (4) is shown in Fig. 2 when the turbulence strength varies from weak to strong with the parameter .

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The probability density function (PDF) of gamma–gamma models in different turbulence conditions.

The THz communication system based on THz QCL and THz QWP uses two off-axis parabolic mirrors in the wave propagation path to collect the optical energy and change the optical path.^[15] Therefore, there is approximately no geometrical spreading loss in the system and it can be negligible. Path loss caused by atmospheric absorption and some additional loss including transmission loss through the polyethylene medium windows and reflection loss from the mirrors are considered. Then the total atmospheric attenuation can be express as

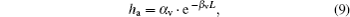
The LDPC code is a special linear group of codes with very sparse parity-check matrix. Many constructor methods for the parity check matrix and efficient encoding schemes with linear time have been proposed.^[21–23] In this paper, the quasi-cyclic LDPC codes presented by IEEE 802.16e standard are adopted to analyze the coding gain in different conditions as a reference.^[24] The LDPC codes are constructed by the base check matrix and encoded by an iterative encoding method with linear time encoding complexity.

The LDPC soft decision decoding algorithm is also a crucial point to optimize the system performance. The first step of decoding algorithm is the initialization step, which must calculate the knowledge of the log-likelihood ratio (LLR) for each received incident information bit y at the transmitted bit x = {0,1},^[25]

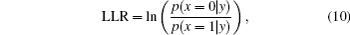
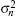
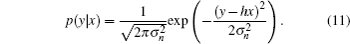
It is assumed that perfect channel side information (CSI) denoted by h in Eq. (1) is known and is a constant in time interval of every information bit. Without loss of generality, let us assume the responsivity R = 1. In the case of OOK modulation, the atmospheric fading channel can be considered as an equivalent memoryless AWGN channel of variance with a discrete transmitter alphabet x = {0,1} and a continuous received alphabet y, which conditional PDF of the received signal is given by^[7]

Assume that “0” and “1” are transmitted in identical probability, then we can derive the priori LLR expression from Eqs. (10) and (11)

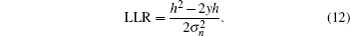
After the initialization step, the iterative LDPC decoding operates by passing messages between variable nodes and check nodes according to the equivalent Tanner graph of the parity check matrix until correcting the error bits or reaching the maximum iterations.^[10]

To illustrate BER performance of LDPC codes in THz wireless channel through atmosphere, plenty of numerical simulations have been carried out. The key values in the simulations are based on practical channel parameters obtained from experimental scenario, as shown in Table 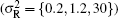1. For comparison of LDPC codes with different parameters, we considered two different code rates (R = 1/2 and R = 2/3) and two different code lengths (n = 960 and n = 1920). And different atmospheric turbulence intensities from weak to strong are also considered. To demonstrate the improvements of performance with LDPC codes more visually, the relationship between SNR and propagation distance or data bit rate have been presented. The LLR-BP algorithm is applied to decode the LDPC codes according to the initialization formula in Eq. (12), and maximum iterations is set to 50. When the information bits are uncoded, hard decision is used for demodulation.

Table 1.

Table 1.

Table 1. Constants and system parameters. . Name Symbol Value Carrier frequency fc 3.9 THz QCL average emission power Pt 2.0 mW QWP responsivity R 1 A/W Extinction coefficient βv 1.5 dB/m Additional loss αv −3 dB Boltzmann constant kB 1.38 × 10−23 J/K Ambient temperature T 300 K Load resistance RL 10 kΩ Noise figure Fn 10 dB Propagation distance L 15 m∼30 m Bit rate Rb 1 Mbps∼100 Gbps

Table 1. Constants and system parameters. .

The simulation results are shown in Fig. 3. Figures 3(a)–3(c) correspond to weak, moderate, and strong atmospheric turbulences with parameter , 1.2, and 30, respectively. And figure 3(d) illustrates the variation of SNR at the receiver with the propagation distance and data bit rate. From Fig. 3(a), the LDPC coded system outdistances the uncoded system on performance more than 10-dB coding gain in weak turbulence when achieving the same BER = 10⁻⁴. The coding gain of the rate 1/2 LDPC code with respect to the rate 2/3 LDPC code in the same code length 960 bits is 1.4 dB at the same BER = 10⁻⁴. When attaining BER = 10⁻⁴, the coding gain of the code length 1920 bits LDPC code is superior to that of the code length 960 bits LDPC code in the same rate 1/2 about 0.6 dB. Similar conclusions can be obtained from Figs. 3(b) and 3(c) in moderate and strong turbulences, respectively. Combined with Figs. 3(a), 3(b), and 3(c) for comparison, the BER performance of THz wireless communication system deteriorates rapidly whatever it is LDPC coded or uncoded, as the turbulence intensity gets stronger and stronger. It is obvious that the uncoded system gets worse faster than the LDPC coded system. The coding gain between 960 bits LDPC at rate 1/2 and rate 2/3 has larger difference in quite stronger turbulence conditions. In the contrary, the coding gain between 960 bits and 1920 bits LDPC at rate 1/2 exhibits no obvious changes at different atmospheric turbulence. It demonstrates that the code rate plays a more important role than the code length in excellent LDPC codes construction. From Fig. 3(d), SNR at the receiver decreases rapidly as the propagation distance or bit rate increases. In the condition of target bit rate beyond 1 Mbps, the THz wave can propagate at most 30 m due to great atmospheric absorption coefficient. When the propagation distance is over 30 m, SNR at the receiver will decrease to 10 dB or less, in which case the real signal can not be recovered from the noise. It reveals that THz wave is more suitable for short distance communications like indoor scenario. Focusing on the propagation distance at 25 m, we can see SNR at the receiver is around 20 dB and 10 dB when bit rate is 100 Mbps and 1 Gbps, respectively. In the same reason, when the bit rate reaches 10 Gbps at distance 20 m, SNR at the receiver is 15 dB. However, according to the Figs. 3(a), 3(b), and 3(c), the minimum SNR required in the THz communication systems with rate 1/2 LDPC codes reaching the best performance is 10 dB, 12 dB, and 14 dB, respectively. This means in such systems the bit rate can achieve 10 Gbps or more at communication distance 20 m. In the contrary, the minimum SNR that uncoded system requires expects to be 25 dB or more in the same distance 20 m and that directly results in the bit rate will not exceed 1 Gbps. Therefore, we can conclude that the system with LDPC codes can really increase the bit rate even beyond 10 Gbps through atmospheric wireless channel in a large degree.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Performance of LDPC codes with different turbulence condition, propagation distance and bit rate. (a) Turbulence intensity , (b) turbulence intensity , (c) turbulence intensity , and (d) SNR of receiver with propagation distance and bit rate.

From simulation results and evaluation, we can see adverse impact caused by atmospheric absorption and scintillation is evident in THz communication system. LDPC codes can be an efficient solution to improve the BER performance and increase the communication distance and data rate. The THz wave is quite suitable for ultra-high speed indoor wireless communications and its data bit rate can be expected to exceed Gbps in LDPC coded systems. Large code length and low code rate LDPC codes are recommended in THz wireless communication. However, longer code length and lower code rate will result in a longer latency and information transfer rate. The longer block lengths increase the system implement complexity and hardware resources and reduce data throughput for high speed data transmission. Under the condition of abundant bandwidth resources, a rational LDPC code should be chosen to apply to practical THz wireless applications considering system complexity, data rate, and transmission delay, besides BER performance.

In conclusion, we present an efficient error control coding scheme based on powerful LDPC codes over a THz wireless link through atmospheric channel with THz QCL as emitter and THz QWP as detector. The introduction of LDPC codes as the channel coding is proved to be considerably significant to reduce the atmospheric attenuation and turbulence effects. Meanwhile, LDPC codes contribute great improvements on THz communication distance and data bit rate and the overall transmission rate is promised to be beyond Gbps. Though LDPC codes might have some disadvantages, they still can be a promising and potential solution to develop the practical applications in THz indoor wireless communications along with the rapid development of integrated circuit, semiconductor device, and manufacture technology.