As a bridge between atom/molecule and solid, a cluster represents a distinct form of matter and shows specific properties intermediate between individual atom and bulk matter.^[1–5] The cluster-surface interaction has attracted a great deal of research attention in recent years,^[6–13] due to its fundamental importance to varieties of applied processes, such as deposition, implantation, and growth of high-quality ultrathin films. Some former studies were performed experimentally with clusters energies from hundreds of eV to some keV, and important aspects on the stability of a cluster, and charge transfer have been revealed.^[10,14–23] Information on the stability of the cluster, even the fragmentation pattern can be obtained by looking at the outgoing fragments.^[24–28] In some aspects, one may need to consider the dynamics motion of atom/clusters with velocities up to several hundreds of km·s⁻¹ scattering from the crystal surface under small angles of incidence, e.g., some adsorbed gas molecules and copper atoms washedout from the wall may interact with the surface in the magnetic compression system.^[29,30]

It was reported that the dynamic motions of clusters may be affected by an atomically well-defined surface during cluster–surface interaction.^[1] The experimental studies can be reached easy adopting a chemically inert substrate like highly ordered pyrolytic graphite (HOPG), and extreme clean vacuum conditions. However, experimental observations represent only the final products of the collision process. In contrast, the molecular dynamics (MD) simulation depicts the entire collision process with high spatial and temporal resolution.^[7] Thus, the MD simulation technique is an important tool in the cluster–surface research field,^[31,32] and has become an effective complement of experimental research.^[33] The theoretical studies of cluster–surface mainly focus on the deposition of a cluster, implantation, and surface modification.^[7,34–41] In these previous studies, the influence of the surface structure on the whole interaction process is rarely discussed, because of the existence of the computational bottleneck of the size of the crystal required to properly describe the cluster while in contact with the surface. The bottleneck becomes remarkable if the cluster scatters under small angles of incidence. Accordingly, the initial conditions of adopting an amorphous target without a detailed description of its structure, using a rigid wall as the target or limiting the study normal to the surface plane are usually chosen in MD study to mimic the experimental situation, which means that the further improvement of clusters scattering from the crystal surface is still expected.

Motivated by previous studies, by introducing a new technique to obtain the periodic boundary condition, the dynamic motions of copper clusters Cu_n with velocities ranging up to hundreds of km·s⁻¹ scattering from a single-crystal Cu (111) surface are studied. We try to find the dependence of the stability of clusters on velocities, angles of incidence, cluster sizes, and surface structure. The paper is organized as follows: in the following section, the modelings of MD simulations including the dynamics motion of clusters, fragmentation determination are described. The results and discussions are given in Section 3. The conclusions of this work are summarized in the last section.

In the present simulation, the magic-sized Cu₁₄₇ and random-sized Cu₁₀₀ clusters are adopted as projectiles.^[42] Unlike the single atom scattering based on binary collision approximation, the description of cluster scattering is relative to a large amount of interactions occurring not only between the cluster and the surface, but also for other atoms inside the cluster.

Previously, in order to deduce the velocity-dependent stopping power from the collisions of projectile with surface electron gas, the energy loss of clusters scattering from the surface was reported in Ref. [43]. Actually, when the clusters scatter from the surface with finite parallel velocity, the atom–target attractive potential may lag behind the projectile, leading to an additional force opposite to the direction of the projectile’s velocity. In this case, the electron energy losses do not represent purely from the influence of surface electron gas. Thus, the attractive potential of projectile–surface interaction has to be excluded, and only the repulsive potential is adopted to describe the interactions between projectiles and the surface. However, when the projectiles are in close contact with the surface, the continuum potential is not accurate enough to describe the interaction of projectile–surface any more. More accurate descriptions of projectile–surface interaction are required.

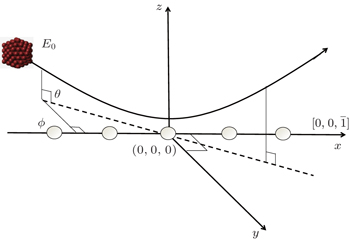
For cluster–surface scattering, an atom i inside the cluster at a distance R above the surface is subjected to three forces:

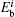
The term F_TFM(R) stands for the Coulomb force between projectile and surface, and can be given by:

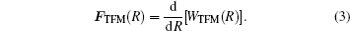
In order to simplify the calculation, when R > r_cutoff, the Coulomb interaction can be approximated by a continuum potential:

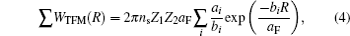
The true computational bottleneck in the simulation is the size of the copper crystal, which is required to describe properly the clusters in contact with the surface. The periodic boundary condition can be obtained by establishing a huge crystal surface. Under such conditions, however, the consumption of computer resources is enormous when the cluster is in close contact with the surface. More computer resources are depleted for clusters scattering under small angles of incidence, since more target atoms in the path that clusters glide along will be taken into account. For simulating scattering of single atoms from the surface, this bottleneck may be handled simply by introducing periodic boundary conditions: when the single atom reaches the end of a target, it will reappear at the very opposite end of the slab.^[47] Nevertheless, this technique cannot be implemented easily for large molecules scattering from the crystal surface.

Because the time development of the cluster positions and velocities needs to be traced, establishing a dynamic target may be the only way to achieve the periodic boundary condition. For single atom scattering, the atom–surface potential is well approximated by summing up all the potential of 75 target atoms lying nearest to a projectile.^[48] Thus, the nearest 75 atoms to the atom “i” instead of the whole surface plane are involved in the calculation of the interaction, which is expected to save much of the computer resources.

In the present work, the process of obtaining the periodic boundary condition is separated into three steps.

Step 1 The description of the surface structure of the 75-atom target was shown in Ref. [49], and the coordinate system is set in the scattering plane with the x, y axis parallel to the surface, and z axes perpendicular to the surface. For the purpose of defining the azimuthal angle, the x axis is placed exactly on the lattice orientation [1,0,], as shown in Fig. 1. Then, a large target including 2307 atoms distributed evenly in three layers was generated. The target₂₃₀₇ is the key for: (i) obtaining the schematic diagram of the cluster scattering; (ii) marking the coordination x_closest(i) and y_closest(i).

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Sketch of the coordinate system.

Step 2 The copper clusters were placed in the center above target₂₃₀₇, and the coordinations x_closest(i) and y_closest(i) of the target atom closest to the copper atom i are marked. Afterwards, n targets, i.e., target(1), target(2), …, target(i), …, target(n), including 75 atoms are built. The coordinate system along the x–y surface plane of target(i) was set exactly in the point with the coordinations of x_closest(i), y_closest(i). At the mean time, the thermal vibrations of target atoms of target(i) are taken into account using random displacements based on the Debye model.

Step 3 As soon as the atom i moves out of the range of target(i), the coordination of x_closest(i), y_closest(i) were marked again as the coordination of the target atom, which is closest to the copper atom i. Then, the target(i) with new thermal vibrations displacements is generated again, and its coordinate system is set right in the point of x_closest(i), y_closest(i).

By continuously repeating Step 3, the random thermal vibrations of every target atoms are implanted, and the copper clusters seem to scatter from an infinite surface plane. Using this technique, the calculation of the attractive potential of an atom i at a distance R_i < r_cutoff and repulsive potential of an atom j at distances R_j > r_cutoff above the surface is involved simultaneously. Then, the MD simulation of cluster scattering from the crystal surface under small angles of incidence can be performed with PC computer resources.

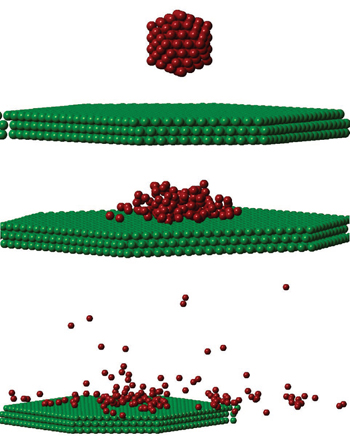
Using the above modelings, the cluster’s motions are solved numerically by a stepwise integration of Newton’s equations of motion, using 1 a.u. (The unit a.u. is short for atomic unit) steps. By analyzing from the sets of 1000 trajectories, the time development of the atom inside the cluster was memorized during the MD study, and a fragment is defined as a group of atoms each of which has no interaction with some other numbers of the group at the end of the simulation. This definition, however, indicates that some fragments may include rather weakly bounded atoms.

Fig. 2 shows snapshots from a simulated fragmentation process for Cu₁₄₇ scattering with an angle of incidence with respect to the x–y surface plane from a single-crystal Cu (111) surface under an azimuthal angle with respect to the [1,0,] direction. These snapshots were taken at the distance of 30 a.u. from the topmost of layer in the approaching phase, the distance of closest approach, and almost the end of simulation, respectively. It is noted that some fragments are already out of the range of the crystal surface after scattering. Actually, during the simulation process, the copper atom i interacts with corresponding target(i) with 75 atoms. The target₂₃₀₇ was implemented in these snapshots only for the purpose of obtaining the schematic diagram of cluster scattering. As shown in the lowest panel of Fig. 2, even though the incident energy is far larger than the individual bond energies of 3.388 eV/aotm, some copper atoms still stick together, leading to the formation of fragments.

Fig. 2.

	Figure Option ViewDownloadNew Window
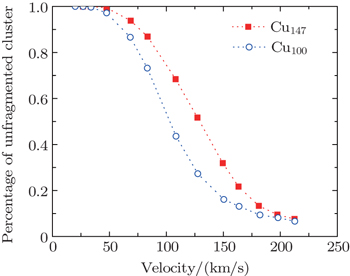
	Fig. 2. Snapshots of a Cu147 cluster with velocity 127 km·s−1 scattering from the Cu (111) surface under an angle of incidence θ = 1°. The azimuthal angle is chosen as ϕ = 3°. From top to bottom: before, during, and after scattering.

The stability of fullerenes was found as a function of impact energy and the size of fullerenes in Ref. [50], where the percentage of unfragmented fullerenes even goes down to zero. In the present work, the percentage of the unfragmented cluster is defined as N_largest/N_o, where N_largest, N_o denote the number of atoms in the largest fragment and the original cluster, respectively. The largest fragment is the specific one having the maximum atoms, and preserving the properties of the original cluster at the most.

In Fig. 3, the percentage of cluster that remains unfragmented was shown as a function of the velocity for which no fragmentation takes place to the range of producing full atomization. The Cu₁₄₇ with an icosahedral structure appears more stable with respect to fragmentation than the random size of Cu₁₀₀. Since N_largest is equal to 1 for full atomization of Cu₁₄₇ scattering, the unfragmented percentage will be 1/147. Thus, the percentage of unfragmented cluster will not go down to zero even though the full atomization of the cluster occurs. This feature is different from the results of Ref. [50], in which the way of defining fragments was not shown clearly.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Percentage of unfragmented cluster as a function of velocity for Cu100, Cu147 scattering from Cu (111) surface under an angle of incidence θ = 1°. The azimuthal angle was chosen as ϕ = 3°. The lines are drawn to guide the eyes.

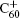
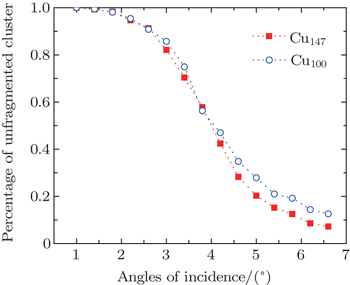
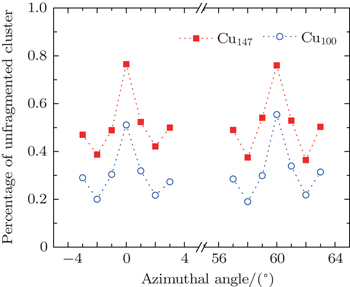
A threshold impact energy of 2.5 eV/atom for C₆₀ shattering into fragments after impacting on a structureless wall had been reported in Ref. [50]. Even though the perpendicular energy is smaller than threshold energy, the fragmentation of ions via a sequential C₂–loss process does occur.^[50] In the present work, the critical velocities with respect to fragmentation process are about 26.9 km·s⁻¹, 33.59 km·s⁻¹ for Cu₁₀₀, Cu₁₄₇, respectively. Accordingly, the threshold impact energies are 240 eV/atom and 374.15 eV/atom for Cu₁₀₀, Cu₁₄₇ scatterings. The threshold impact energies are far larger than those of C₆₀, and the Cu–Cu bond energy of 3.388 eV/atom.

The percentage of unfragmented cluster as a function of angles of incidence for Cu₁₀₀, Cu₁₄₇ scattering from the Cu (111) surface is shown in Fig. 4. According to Figs. 3 and Fig. 4, the Cu_n clusters dissociate into fragments when incident velocities and angles of incidence are larger than a critical value. The vertical energy can be achieved by E_⊥ = E_o × sin²(θ), where E_o is the incident energy, and θ denotes the angle of incidence. For increasing impact energies and angles of incidence, larger vertical energies lead to more intensive fragmentation of a cluster. Accordingly, the threshold vertical energies are 0.073 eV/atom, 0.114 eV/atom for Cu₁₀₀, Cu₁₄₇ in the case of Fig. 3, which are much smaller than the bond energy of 3.388 eV/atom.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Percentage of unfragmented cluster as a function of angles of incidence for Cu100 with 30.08 km·s−1, Cu147 with 35.09 km·s−1 scattering from the Cu (111) surface, respectively. The azimuthal angle was chosen as ϕ = 3°. The lines are drawn to guide the eyes.

As mentioned above, because of the existence of the computational bottleneck in implementing the periodic boundary condition, some previous works replaced the crystal with a rigid wall or limited the study along the surface normal.^{[37,47,50,52–55]} Actually, the angle of incidence in experimental study may be typically chosen as 70°,^[47] and it even may be chosen as several degrees in grazing incidence studies.^{[14,15,56,57]}

For the scattering of fast atoms and ions from the surface under small angles of incidence, the motions of the projectiles have been proven to proceed in the regime of “surface channeling”,^[58–60] i.e., projectiles are steered in terms of small angle collisions by atoms of the topmost layer of the surface. When the direction of the incident beam coincides with low-index directions along the surface plane, scattering can occur along strings of surface atoms in the regime of “axial surface channeling”.

A shown in Fig. 5, the influence of surface structure on fragmentation outcomes was studied under different azimuthal angles with respect to the low-index direction [1,0,] of the surface plane. Then, the projectiles are steered in the regime of “axial channeling” under azimuthal angles of ϕ = 0° or ϕ = 60°. Otherwise, the “planar channeling” occurs if projectiles scatter along random directions.

In the previous works, the influence of surface structure on ion/atom-surface interaction was studied by observing the energy loss, electron yield,^[61] x-ray yield and fluctuant final charge-state fractions.^[49] From Fig. 5, the percentage of unfragmented clusters was enhanced for clusters scattering along low-index directions.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Percentage of unfragmented cluster as a function of azimuthal angles for Cu100 with a velocity of 127.62 km·s−1, Cu147 with a velocity of 127.31 km·s−1 scattering from the Cu (111) surface, respectively. The angles of incidence θ were chosen as 1 degree in both cases. The lines are drawn to guide the eyes.

The phenomenon dependent on the lattice orientation directions of the surface plane is similar to that of individual atom/ion scattering, in which the screened Coulomb potential is adopted to describe the interaction between projectile and target.^[58] Some facts can be summarized from this phenomenon. (i) The influence of the channeling effect is pronounced for large cluster scattering. Similar to atom/ion scattering, the cluster will meet the lattice strings under axial channeling geometry, and then undergoes a sequence of successive collisions with atoms of lattice strings. In other words, the cluster encounters soft collisions with atoms along lattice strings. In contrast, when the cluster scatters along random directions, it will interact with the whole surface plane and then undergoes harder collisions. As a consequence, the fraction of unfragmented cluster is higher for ϕ = 0° and ϕ = 60°. (ii) During approaching the surface phase, the distance of the closest approach is about 2.33 a.u. According to the TB-SMA potential, the cut-off distance between Cu–Cu atoms is about 13.23 a.u. Since the diameter of Cu₁₄₇ is about 30 a.u., when a group of atoms is in the range of surface attractive potential, other groups of atoms are still in the range of surface repulsive potential. Then, in channeling conditions, the target surface affects the cluster by attracting and repelling it simultaneously, which is different to single atom scattering. In Ref. [43], only the repulsive potential was adopted during the whole approaching surface phase. The result indicates that if all atoms of a cluster are repelled by the target surface, the channeling effect is not obvious by looking at the fragment outcomes.

Figure 6 shows the number distributions of fragment for two clusters scattering under different azimuthal angles. If the clusters can survive without fragmentation, the number of fragments will be noted as 1. However, if the full atomization of clusters occurs after scattering, the number of fragments will be noted from 1, …, n, where n is the atomic number of incident clusters. For example, by analyzing the sets of 1000 trajectories, the intensity of fragment distributions will be 1000 in the site of 147 for full atomization of Cu₁₄₇ scattering. Normally, at the range where any fragmentation occurs but without leading to full atomization, the number distribution of fragments is observed from 1000 at low range to 0 at high range. According to the definition, the number distribution of fragments will shift to the higher range if the clusters undergo more intensive impact. Thus, when Cu₁₀₀, Cu₁₄₇ clusters scatter along random direction ϕ = 3°, the number distribution of fragments shifts to the right side, indicating the clusters undergo a more intensive fragmentation process.

Fig. 6.

	Figure Option ViewDownloadNew Window
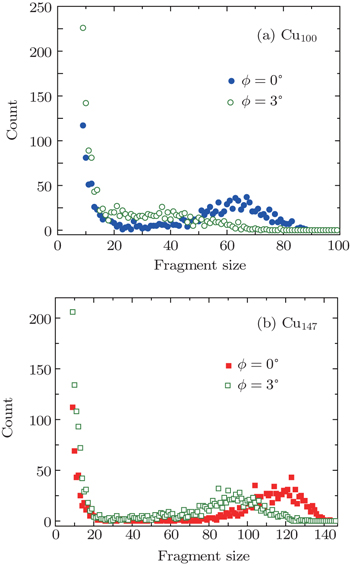
	Fig. 6. The number distributions of fragments for (a) Cu100 with velocity of 127.62 km·s−1, (b) Cu147 with velocity of 127.31 km·s−1 scattering under azimuthal angles of ϕ = 0°, 3°, respectively. The angles of incidence θ are chosen as 1° in every case.

Based on Fig. 5, two azimuthal angles of ϕ = 0°, 3° at which they are accompanied by fragmentation but without leading to full atomization of clusters are adopted to observe the distribution of fragmentation outcomes. The fragment outcomes in each size for Cu₁₄₇ cluster scattering from the Cu (111) surface under two azimuthal angles are shown in Fig. 7. It is obvious that the count numbers of fragmentation outcomes in small size are enhanced for clusters scattering along random directions, indicating that the clusters undergo further fragmentation. It is noted that an additional peak appears around the fragment size of Cu₁₂₀ for clusters scattering along the low-index direction.

According to Fig. 7, the count numbers of small fragments Cu_n (n = 1–5) are much enhanced, compared to that of other fragment outcomes. Therefore, in order to explore more detailed information on other fragment outcomes, only the fragments consisting of 9–100 atoms for Cu₁₀₀ projectiles, and 9–147 atoms for Cu₁₄₇ projectiles are shown in Fig. 8. The main features of the fragment distributions can be summarized as follows.

Fig. 7.

	Figure Option ViewDownloadNew Window
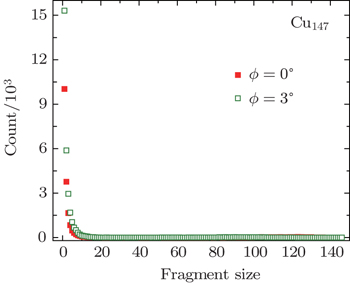	Fig. 7. Fragment distributions of Cu147 clusters with velocity of 127.31 km·s−1 scattering along directions of ϕ = 0°, 3°, respectively. The angles of incidence θ were chosen as 1°.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Fragment distributions of (a) Cu100 with a velocity of 127.62 km·s−1, (b) Cu147 with a velocity of 127.31 km·s−1 scatterings under azimuthal angles of ϕ = 0°, 3°, respectively. The angles of incidence θ are chosen as 1°.

As mentioned above, most of the previous works were done by replacing the crystal with a structureless wall or limiting the study along the surface normal, in order to make the simulation consume modest computer resources. Some studies indicate that qualitative results are not sensitive to the details of the wall description or to its lack of atomic structure.^[62] By implanting a new technique to obtain the periodic boundary condition, the influence of crystal surface with detailed descriptions of lattice orientation on the scattering of clusters is discussed in the present study. The qualitative results show that the stability of cluster and the fragments distribution are sensitive to the detailed description of crystal surface.

A molecular dynamics simulation of Cu_n clusters scattering from a crystal surface under small angles of incidence has been presented. We have found that the percentage of unfragmented cluster, the distribution of fragmentation products are strongly dependent on incident energies, angles of incidence, and lattice orientation of the crystal surface. The copper clusters appear to be more stable under an “axial channeling” scheme. When the cluster is in close contact with the surface, the target surface attracts and repels the cluster simultaneously. Consequently, the channeling effect becomes obvious. The dissociation schemes of the copper clusters Cu₁₀₀, and Cu₁₄₇ are discussed under different channeling conditions. The fragmentation of Cu₁₄₇ occurs via successive “knockouts” of small fragments, and it is reasonable to believe that the information on the crystal surface can be explored by looking at the fragment distribution of dissociation products.