Memristors, namely resistors with memory, have attracted much recent attention due to their ability to keep track of the past resistance state through which the element has experienced.^[1–3] With inspiration from the discovery of memristor, the memory counterparts of capacitor and inductor, known as memcapacitor and meminductor, respectively, have also been proposed.^[4] These circuit elements with memory, or memelement for short, when combined in complex circuit networks, can perform logic, arithmetic operation, and neuromophic computing in a massively parallel fashion, a striking resemblance with functionalities of human brain.^[5–7] From symmetry concerns in circuit theory, there should a fourth fundamental circuit element in addition to the three well-known elements (resistor, capacitor, and inductor), which is defined directly from a relationship between charge q and magnetic flux φ. Accordingly, a memory counterpart to the fourth circuit element could also be conceived. The conjectured fourth memelement, in parallel to the memristor, memcapacitor, and meminductor, may further promote the functionalities of complex circuit networks, but has not yet been actualized in real devices.

Historically, the fourth fundamental circuit element was assigned to the memristor proposed by Chua in terms of the nonlinear i–v relationship with a pinched hysteresis loop,^[8,9] as he was not aware of any device showing a direct φ–q relationship at that time. Nearly 40 years later, HP researchers demonstrated the memristor behavior in a metal/oxide/metal sandwiched structure that exhibits a hysteretic i–v curve.^[10] This discovery spurred intensive interests in investigating resistance switching memories.^[11,12] Furthermore, Chua argued that all the two-terminal nonvolatile memory devices based on resistance switching are memristors, regardless of the materials applied or physical mechanisms in operation.^[13] However, it seems that the memristors based on resistance switching do not correlate charge q and magnetic flux φ directly as would expected for the fourth element by original definition. This point has been questioned by Vongehr et al. who recently claimed that the real memristor is still missing and likely impossible.^[14] Also, Mathur commented that the memristor should not be the fourth element because of the absence of magnetic flux.^[15]

Recently, a new fourth fundamental circuit element based on the magnetoelectric (ME) effects, dubbed transtor, has been proposed by us.^[16] The ME effects refer to the change of electric polarization (magnetization) by applying a magnetic field (electric field), which have been observed in a variety of materials, especially multiferroic materials.^[17,18] The transtor employing the ME effects can directly link q and φ by

The memory counterpart to transtor, dubbed memtranstor (M_T), which can memorize the past dynamics between q and φ, has also been predicted^[16] A memtranstor is defined by

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. (a) The complete relational diagram of all the possible two-terminal fundamental circuit elements, each defined by a direct relationship between two basic variables. It consists of four linear elements, the resistor (R), the capacitor (C), the inductor (L), the transtor (T), and four nonlinear memelements, the memristor (MR), the memcapacitor (MC), the meminductor (ML), and the memtranstor (MT). Symbols for transtor and memtranstor are introduced to facilitate later usage. (b) Schematic illustration of the memtranstor behaviors. The butterfly-shaped hysteresis loop is expected to occur at a sufficiently large input of q or φ.

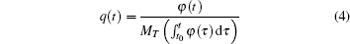
The memristor, memcapacitor, and meminductor are always characterized by a pinched hysterestic loop dwelling in the I–III quadrants, due to the positive values of resistance, capacitance, and inductance, respectively. In contrast, the transtance defined in Eqs. (1) and (2) can be either positive or negative, depending on the sign of the ME coefficient α that can be negative due to breaking of time reversal symmetry in the linear ME effects. Therefore, the characteristic hysteresis loop of the memtranstor could lie in either the I–III quadrants or the II–IV quadrants.^[16] Especially, a unique butterfly-shaped hysteresis loop could be anticipated following the sign reversal of transtance driven by a sufficiently large input of charge or flux intensity, as shown in Fig. 1(b). The fourth linear element, transtor, can be easily realized by using a magnetoelectric material showing linear ME effect, such as Cr₂O₃ (see Fig. 2 in Ref. [17] and the inset of Fig. 3(b) in Ref. [18]). However, the memtranstor is much more difficult to be actualized because a special nonlinear ME effect with memory has to be required. In this work, we demonstrate the memtranstor behavior in a real device at room temperature, by virtue of the nonlinear ME effect in a magnetoelectric Y-type hexaferrite.

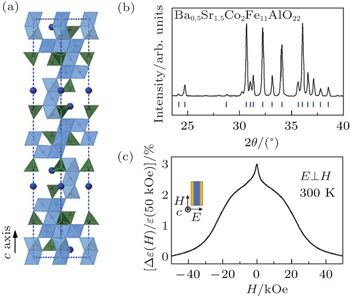
Polycrystalline ceramics of the Y-type hexaferrite Ba_0.5Sr_1.5Co₂Fe₁₁AlO₂₂ (BSCFAO) were prepared by solid-state reaction method. Stoichiometric amounts of SrCO₃, BaCO₃, Co₃O₄, Fe₂O₃, and Al₂O₃ were thoroughly mixed and ground together, calcinated at 940 °C in air for 10 h. The resulting mixture were reground, pressed into pellets, and fired at 1200 °C for 24 h in oxygen atmosphere. Subsequently, as-sintered samples were annealed in a flow of oxygen at 900 °C for 72 h and then slowly cooled down at a rate of 40 °C/h. The phase purity was checked by powder x-ray diffraction using a Rigaku x-ray diffractometer.

The BSCFAO sample was cut into a regular plate with a size of 2.36 mm × 2.36 mm × 0.39 mm and a mass of 0.012 g, and silver paste was painted on the widest faces as electrodes to form a simple two-terminal device. The magnetoelectric current and dielectric properties were measured by using an electrometer (Keithley 6517B) and an LCR meter (Aglient 4980A), respectively, in a Cryogen-free Superconducting Magnet System (Oxford Instruments, TeslatronPT). Before the measurement of magnetoelectric current, the device was poled in E = 5 kV/cm from 50 kOe (1 Oe = 79.5775 A·m⁻¹) to 2 kOe to drive the sample from paraelectric to ferroelectric state. Then the poling electric field was cut off, and the current released from the electrods was measured as a function of scaning magnetic field. The magnetic properties were measured by using a superconducting quantum interference device magnetometer (Quantum Design MPMS-XL).

The hexaferrites are a family of old magnetic materials but are attracting renewed interests due to their strong ME effects arising from the ferroelectricity induced by the conical or helicoidal spin configurations.^[19–24] Here, we utilize a Y-type hexaferrite with a nominal formula of Ba_0.5Sr_1.5Co₂Fe₁₁AlO₂₂ (BSCFAO) that exhibits clear ME effects even at room temperature. The crystalline structure of the Y-type hexaferrites consists of alternate stacks of superposition of spinel blocks (S) and the so-called T-blocks with space group of R3m, as illustrated in Fig. 2(a). Earlier studies have shown that many Y-type hexaferrites possess helical magnetic structures with wave vector k along c axis at certain temperatures and magnetic fields applied in ab plane can drive it into transverse conical spin configurations.^[25–27] These transverse conical spin configurations in the Y-type hexaferrites have been experimentally and theoretically proven to be ferroelectric states.^[19–21] Figure 2(b) shows the powder x-ray diffraction patterns at room temperature of the polycrystalline sample of BSCFAO. All the diffraction peaks can be assigned to the Y-type hexaferrite structure and no secondary phase is observed.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (a) The crystal structure of the Y-type hexaferrite BSCFAO. (b) The XRD pattern of the polycrystalline BSCFAO samples at room temperature. The blue lines represent the standard peak positions. (c) The relative change of dielectric constant as a function of magnetic field at 300 K. The inset shows the measurement configuration.

We then made a two-terminal device in which a thin plate of BSCFAO hexaferrite is sandwiched between two parallel silver electrodes to testify the memtranstor behavior. The magnetic field was applied along the in-plane direction and perpendicular to the electric field, forming a transverse magnetoelectric configuration (see the inset in Fig. 2(c)). The magnetic-field dependence of the relative change of dielectric constant of the device at room temperature, defined as ε(H), is shown in Fig. 2(c). As magnetic field increases, the dielectric constant shows a steep drop up to ∼ 3 kOe, gently decreases from ∼3 kOe to ∼33 kOe and then becomes nearly constant above ∼33 kOe. This dielectric variation in BSCFAO is in accordance with its magnetization change with magnetic field. As shown in Fig. 3(a), the magnetization increases rapidly from 0 kOe to ∼3 kOe, gently increases from ∼3 kOe to 33 kOe, and then is almost saturated above 33 kOe. These features can be interpreted by the transition from longitudinal spin cone with paraelectricity to transverse spin cone with ferroelectricity, and then to the collinear ferrimagnetic phase. This indicates that the ferroelectric phase due to transverse cone in this specimen can be easily induced by low magnetic fields and persist under relatively large H at room temperature. The M–H curve in the low magnetic field region is shown in the inset of Fig. 3(a). The small coercive field of ∼0.35 kOe might be due to the weak in-planar magnetic anisotropy. This M–H curve will be compared with the q-φ relationship of the device later.

The magnetoelectric current was measured by sweeping H from 2 kOe to −2 kOe by passing through the zero-H continuously and then back again. Prior to the respective measurements, the device was poled from 50 kOe to 2 kOe with electric field E = 5 kV/cm to drive the sample from paraelectric to ferroelectric state. Figure 3(b) shows the variation of magnetoelectric current with sweeping magnetic field H. The magnetoelectric current curves have symmetric shapes and show remarkable dip and peak structures. The electric polarization obtained by integrating the magnetoelectric current with time is plotted as a function of magnetic field in Fig. 3(c). Since the measurement result are well repeatable, we select only one magnetoelectric current–H curve to calculate the polarization. Because the magnetoelectric current generated by the change of polarization from zero-field ferroelectric state to high-field paraelectric state is too small to be distinguished from the leakage current, the absolute P value near zero-field cannot be reliably obtained. Therefore, the relative change of polarization ΔP is used in this plot. Moreover, for simplifying discussion, we set the ΔP value at the pinched point between the up- and down-going H sweeping as the origin. It can be seen that the polarization changes with the magnetic field, yielding a non-zero magnetoelectric coefficient (α = dP/dH). Interestingly, the polarization response to H is strongly nonlinear. A butterfly-shaped loop of ΔP–H can be clearly identified with the crossing point of the curves from up-going and down-going H-sweep in the vicinity of H = 0. From point 1 to point 2, α > 0 indicating a positive magnetization in this region. From point 2 to point 3, α gradually becomes negative, indicating that magnetization has been reversed to negative value by H. When H sweeping back from point 3 to point 4, α is still negative, confirming that the negative magnetization was maintained during this process. With H sweeping from point 4 to point 1, α gradually becomes positive, indicating that magnetization has been reversed again to the positive value. The ΔP–H loop can be converted to the corresponding q–φ relationship by the following equations for a transverse configuration memtranstor^[16]

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. (a) The M–H hysteresis loop of BSCFAO at 300 K. The inset shows an expended view of the magnetization in the low-field region. (b) Magnetoelectric current at 300 K. The inset plots the scheme of the device and the measurement configuration. (c) Electric polarization as a function of magnetic field showing a butterfly-shaped hysteresis loop. (d) The corresponding Δq–Δφ relationship of the device.

The microscopic origin of such spin-induced ferroelectricity can be successfully explained by the spin-current and the inverse Dzyaloshinskii–Moriya models.^[28,29] This spontaneous electric polarization at moderate magnetic field can be attributed to transverse conical magnetic structure, just like previous results in other Y-type hexaferrites.^[19–21] In traditional Y-type hexaferrites, the electric polarization P tend to be reversed by a small magnetic field H.^[22–24] However, this transition in Y-type hexaferrites cannot generate butterfly-shaped ΔP–H curve because the sign of α is invariant if both P and H change their sign together. The unique property for the BSCFO ceramic used in this work is that the P is irreversible when sweeping H through zero field at room temperature. Therefore, the ΔP–H curve shows a butterfly-shape that is consistent to the anticipation for the memtranstor behavior (Fig. 1(b)). It worth to note that the memtranstor may be realized by using other magnetoelectric materials such as M- and Z-type hexaferrites that also show nonlinear hysteretic magnetoelectric effects.^[30,31]

In summary, we have successfully demonstrated the memtranstor behavior in a real device made of a magnetoelectric hexaferrite (BSCFAO) at room temperature. This BSCFAO material exhibits a strong nonlinear magnetoelectric effect at room temperature so that an applied magnetic field is able to change the electric polarization in a nonvolatile way. This results in a nonlinear q–φ relationship of the device with a special butterfly-shaped hysteresis loop, in agreement with the anticipated memtranstor behavior. The memtranstor, regarded as the fourth fundamental circuit memelement after the memristor, memcapacitor, and meminductor, will have a great promise in generating more advanced circuit functionalities and should deserve extensive studies in the future.