† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61565004), the Natural Science Foundation of Guangxi Zhuang Autonomous Region, China (Grant Nos. 2013GXNSFDA019002 and 2014GXNSFGA118003), the Guangxi Scientific Research and Technology Development Program, China (Grant No. 1598017-1), the Guilin Scientific Research and Technology Development Program, China (Grant Nos. 20140127-1 and 20150133-3), and the Special Funds for Distinguished Experts of Guangxi Zhuang Autonomous Region, China.
In this study, we propose and demonstrate a broadband polarization-independent terahertz modulator based on graphene/silicon hybrid structure through a combination of continuous wave optical illumination and electrical gating. Under a pump power of 400 mW and the voltages ranging from –1.8 V to 1.4 V, modulation depths in a range of –23%–62% are achieved in a frequency range from 0.25 THz to 0.65 THz. The modulator is also found to have a transition from unidirectional modulation to bidirectional modulation with the increase of pump power. Combining the Raman spectra and Schottky current–voltage characteristics of the device, it is found that the large amplitude modulation is ascribed to the electric-field controlled carrier concentration in silicon with assistance of the graphene electrode and Schottky junction.
Terahertz waves, whose frequencies lie between the microwave and optical range, inherit features from both photonics and electronics. The vibration and rotation levels of many polar molecules fall within the terahertz band and therefore terahertz waves can be used for substance detection. Owing to the low photon energy, terahertz waves are non-ionizing and safe. Compared with the modern wireless communication band, terahertz communication has a high rate, allowing greater capacity wireless transmission of information in real time. It is because of these outstanding physical properties that the terahertz waves have found many important applications in the biomedical field, wireless communication, radar imaging, etc.[1–4] Those applications in turn call for the urgent development of various terahertz functional devices, such as modulators. Modulators are well established and considered as standard devices in the optical realm, but in the terahertz frequency regime, there is an increasing demand for high-efficient, fast and versatile active modulators. The modulator enables information to be encoded on terahertz waves, thus providing potential applications in imaging, telecommunication, and beam shaping. Graphene, an ideal two-dimensional (2D) material with unique band structure and electron transport properties, shows excellent electrical and optical properties and good compatibility.[5] In the terahertz range, the intraband transitions are the dominant cause of terahertz response of graphene, which makes the graphene widely used in the active terahertz modulators. Compared with other modulation strategies, such as the temperature control of VO2,[6] the optical control of silicon,[7] and the electrical control of GaAs,[8] the graphene shows high flexibility, easy integration, fast response, and other outstanding features. Ju et al. studied the tunable plasmon excitations and light-plasmon coupling at terahertz frequencies in graphene micro-ribbon arrays, where over 13% of the absorption modulation depth was experimentally demonstrated at the plasmon resonance at room temperature.[9] Ren et al. exploited the tunability of the Fermi surface of the graphene on a 300-nm-thick SiO2 layer on the silicon substrate (5 Ω·cm∼10 Ω·cm) and realized terahertz modulation, and observed the charge neutral point (CNP).[10] Sensale-Rodriguez et al. realized a terahertz transmittance modulation depth of 15% and reflectance modulation depth of 64% by the electrical control of the conductivity of single-layer graphene with the same pattern but different doping concentration.[11,12] The monolayer graphene on a layer of hexagonal metallic meta-atoms embedded between the extraordinary optical transmission electrodes[13] can modulate the amplitude of the transmitted terahertz wave up to 47% at the resonance frequency.[14,15] Gao et al. reported a ∼50% amplitude modulation of terahertz waves with gated single-layer graphene by use of extraordinary transmission through metallic ring apertures placed right above the graphene layer.[16] Mao et al. presented a broadband terahertz wave modulator with improved modulation depth by cautiously selecting the gate dielectric materials in a large-area graphene-based field-effect transistor, which achieved a modulation depth of 22% in a frequency range from 0.4 THz to 1.5 THz.[17] Among these previous studies, although the interaction between the light and the graphene can be significantly enhanced by using the resonant metamaterial structure, such a modulator is still limited by its operation bandwidth and is polarization-sensitive. Additionally, the fabrication of multilayer structure is complicated and costly, and the high voltage is mostly required.
On the basis of the high conductivity and low insertion loss of the graphene, here we present an optically pumped and voltage-controllable terahertz modulator. With the increase of the pump power of the 445-nm continuous wave (CW) laser, the modulation depth increases and a transition from unidirectional modulation to bidirectional modulation is observed. When the photoexcitation power is 400 mW, this modulator exhibits maximum transmission modulation depths in a range of –23%–62% at frequencies ranging from 0.25 THz to 0.65 THz and small bias voltages ranging from –1.8 V to 1.4 V.
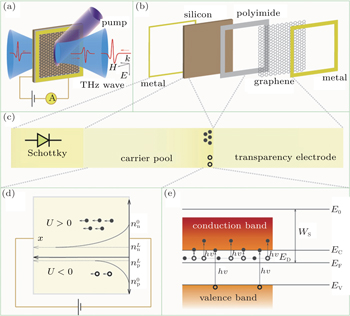
The measurement schematic and detailed structure of the terahertz modulator are shown in Figs.
Raman spectra of the monolayer graphene of the modulator under different optical pump powers and bias voltages were acquired by a Renishaw inVia Raman spectrometer. The Raman excitation light was 514 nm and the excitation power was about several milliwatts. A 50× object lens was used and the integration time of the Raman spectra measurement was 300 s for a spectral range of 1000 cm−1∼3000 cm−1.
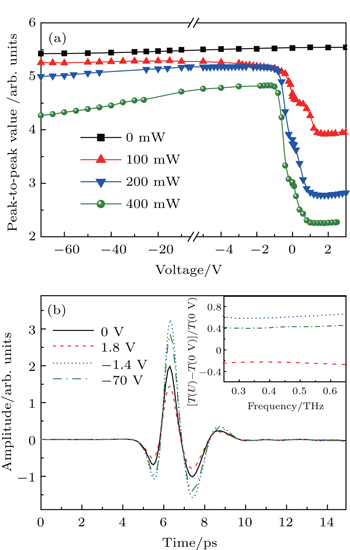
The proposed structure could be actively controlled by the optical power of the pump light and the bias voltage. Figure
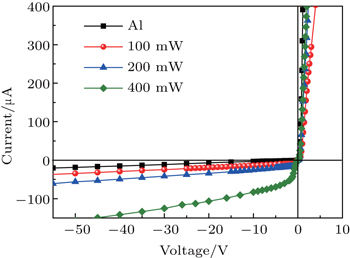
Figure
An equivalent model of the terahertz modulator is proposed as shown in Fig.
Figure
Figure
 | Fig. 4. (a) Reflected and (b) transmitted terahertz time-domain signals from the proposed structure under different photoexcitation powers (0, 100, 200 mW) with zero bias. |
The low-doped n-type silicon in the experiments is a non-degenerate semiconductor and the carrier distribution approximately obeys the Boltzmann law. The carrier diffusion coefficient in silicon can be described by Einstein’s relation as D = (kT/q)μ, where k is the Boltzmann constant, T is the temperature, q is the elementary charge, and μ is the carrier mobility. Owing to the carrier recombination during their diffusion, the concentration of the nonequilibrium carriers of the excited silicon decreases from the surface to the internal (Fig.
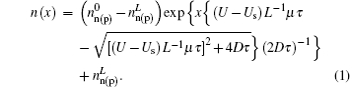

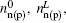
When the Schottky junction is forward-biased, the voltage drop Us is very small, so the applied bias voltage mainly acts on the silicon substrate. The electric field inside the silicon rises rapidly with increasing voltage. The photoinduced holes transmit to the electrode directly while the electrons diffused into the silicon assisted by the electric field. The electric field enhances the electron diffusion, and the electron concentration n(x) is increased. Therefore the substrate carrier concentration n̄ increases rapidly and causes a rapid attenuation of the terahertz transmission, corresponding to the modulation in a voltage range of 0 V–1 V shown in Fig.
When the Schottky junction is reverse-biased, holes would diffuse into the silicon and recombine with electrons, causing the carrier concentration to decrease. The terahertz transmission increases and reaches a maximum at CNP. When the voltage continuously increases in the negative direction, the number of diffusing holes in silicon begins to increase and the conductivity of silicon begins to increase. More photoinduced carriers are generated under a higher optical pump power, and a larger increase of the conductivity of silicon will occur at the same voltage. Thus the transmitted terahertz signal decreases faster at a higher optical pump power. Compared with the strong modulation in a voltage range from –1 V to 1 V, the slight modulation by the voltage below CNP shown in Fig.
In this paper, a broadband and polarization-independent terahertz amplitude modulator based on monolayer graphene on silicon in combination with a Schottky junction is presented. The Schottky junction is used to control the electric field in silicon. By dynamically adjusting the diffusion of the photoinduced carriers in graphene and silicon and thus controlling the carrier concentration in silicon, the modulator shows a significant terahertz amplitude modulation. Under 100-mW photoexcitation of 455-nm CW laser, the modulator operates in the unidirectional modulation mode. Under 400-mW photoexcitation, the modulator exhibits voltage-controlled bidirectional modulation and reaches maximum transmission modulation depths of –23%–62% in the 0.25 THz–0.65 THz range. The modulation depth becomes larger with the increasing of pump power. The modulator can be incorporated into metamaterials to further improve the modulation depth and modulation rate. The proposed design with detailed analysis of carrier concentration in the graphene/semiconductor hybrid structure is great helpful for realizing new efficient active terahertz modulators.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 |