Cite this Article
Chen Qing-Yuan, Huang Yang, Huang Peng-Ru, Ma Tai, Cao Chao, He Yao. Electronegativity explanation on the efficiency-enhancing mechanism of the hybrid inorganic–organic perovskite ABX3 from first-principles study. Chinese Physics B, 2016, 25(2): 027104  
Permissions
Electronegativity explanation on the efficiency-enhancing mechanism of the hybrid inorganic–organic perovskite ABX3 from first-principles study
Chen Qing-Yuan1, Huang Yang1, Huang Peng-Ru1, Ma Tai1, Cao Chao2, He Yao1, †,
Department of Physics, Yunnan University, Kunming 650091, China
Department of Physics, Hangzhou Normal University, Hangzhou 310036, China

 

† Corresponding author. E-mail: yhe@ynu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 61366007, 11164032, and 61066005), the Program for New Century Excellent Talents in University of Ministry of Education of China (Grant No. NCET-12-1080), the Basic Applied Research Foundation of Yunnan Province, China (Grant Nos. 2011CI003 and 2013FB007), and the Excellent Young Talents in Yunnan University, China.

Abstract
Abstract

Organic–inorganic hybrid perovskites play an important role in improving the efficiency of solid-state dye-sensitized solar cells. In this paper, we systematically explore the efficiency-enhancing mechanism of ABX3 (A = CH3NH3; B = Sn, Pb; X = Cl, Br, I) and provide the best absorber among ABX3 when the organic framework A is CH3NH3 by first-principles calculations. The results reveal that the valence band maximum (VBM) of the ABX3 is mainly composed of anion X p states and that conduction band minimum (CBM) of the ABX3 is primarily composed of cation B p states. The bandgap of the ABX3 decreases and the absorptive capacities of different wavelengths of light expand when reducing the size of the organic framework A, changing the B atom from Pb to Sn, and changing the X atom from Cl to Br to I. Finally, based on our calculations, it is discovered that CH3NH3SnI3 has the best optical properties and its light-adsorption range is the widest among all the ABX3 compounds when A is CH3NH3. All these results indicate that the electronegativity difference between X and B plays a fundamental role in changing the energy gap and optical properties among ABX3 compounds when A remains the same and that CH3NH3SnI3 is a promising perovskite absorber in the high efficiency solar batteries among all the CH3NH3BX3 compounds.

PACS: 71.20.Rv;78.20.–e;78.30.Jw;78.40.Me;
Keyword:ABX3;efficiency-enhancing mechanism of ABX3;optical and electronic properties;hybrid perovskite solar cells;
1. Introduction

The hybrid inorganic–organic perovskite absorbers ABX3 (A = CH3NH3; B = Sn, Pb; X = Cl, Br, I) have attracted lots of attention due to their outstanding performances as dye-sensitized solar-cell absorbers, topological insulators, and superconductors.[1–9] The researches of one type of the solar-cell absorber, the hybrid perovskite solar battery, have made great process in the last 5 years.[1–4] Solid-state dye-sensitized solar cells are composed of the semiconducting layer, the sensitizer, the transparent conducting and counter conducting electrodes, and the electrolyte. The working principle of solid-state dye-sensitized solar cells can be summed up as follows:

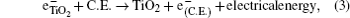
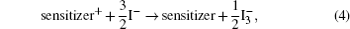
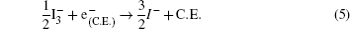
Specifically, we can explain these equations as follows. In order to provide the surface area to adsorb sensitizers, TiO2 is placed on the conducting electrode. When the photons irradiate on them, sensitizers are excited (Eq. (1)). The sensitizer turns into oxide when an electron is injected into the conduction band of the TiO2. This process is described by Eq. (2). The injected electron is transported into the TiO2 and then extracted to a load where the work done is converted into an electrical energy (Eq. (3)). The electron mediator between the TiO2 photoelectrode and the carbon coated counter electrode is electrolytes containing I−/I3− redox ions. Hence the I− ion redox mediator gives electrons to the oxidized sensitizer that makes the oxidized sensitizer regenerated. Then the I− ion redox mediator turns oxide into I3− (Tri-iodide ions), (Eq. (4). The I3− substitutes the internally donated electron with that from the external load, reducing back to I− ion. This process is represented by Eq. (5).[10]

The hybrid perovskite solar battery stands out due to its low cost, high efficiency, and environmental friendliness. Meanwhile, it is becoming a most promising battery compared with various solar batteries. Organic–inorganic hybrid CH3NH3PbX3 (X = Br, I) perovskites were introduced by Kojima et al. in 2009 as a new type of DSC sensitizing material.[11] Lee et al. reported a solution-processable solar cell with a conversion efficiency of 10.9%.[1] The solar conversion efficiency did not increase to 15% till recently, which was reported in a Nature paper by Burschka et al., and its high stability is equal to or even greater than those of the best thin-film photovoltaic devices.[2] As is well known, the ABX3 absorbers with high absorption coefficients will be excellent materials for enhancing the solar-converting efficiency of the solar battery. Previously, the properties of ABX3 were mostly investigated by several experimental studies which claimed that ABX3 is a great solar-cell absorber due to its symmetric structure and electronic properties.[7–13] Nevertheless, theoretical researches of ABX3 are rather rare and incomplete.[11–13]

In this study, we explore the efficiency-enhancing mechanism of ABX3 and systematically investigate the ABX3-type compounds which can stimulate the optical properties for hybrid inorganic–organic perovskite absorbers by first-principles calculations.[14,15] We find that the VBM and the CBM of the ABX3 are mainly composed of anion X p states and cation B p states respectively. The band gap of the ABX3 decreases and the absorptive capacities to different wavelengths of light expands when changing the B atom from Pb to Sn and changing the X atom from Cl to Br to I. Moreover, the organic framework A also plays an important role in ABX3. For instance, with the size of the organic framework A increasing, the band gap increases but atoms B and X remain the same. The changing trend of the band gap will be the same when the atoms B and X change and the size of framework A remains the same. So we just examine the situation where the organic framework A remains unchanged to investigate the efficiency-enhancing mechanism of ABX3 in this work. Finally, it is discovered that CH3NH3SnI3 has the best optical properties, and its light-adsorption range is the widest among all the ABX3 compounds when A remains the radical 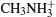situation based on our calculation. We also find that the electronegativity difference between X and B plays a fundamental role in changing the energy gap and optical properties among ABX3 compounds and that CH3NH3SnI3 is a promising perovskite absorber among CH3NH3BX3 compounds in the high efficiency solar batteries.

2. Computational details

Our calculations were performed using the Vienna ab initio simulation package (VASP) with the projector-augmented wave (PAW) pseudopotentials.[16,17] We used the Perdew–Burke–Ernzerhof generalized gradient approximation to treat the exchange–correlation energy of interacting electrons.[18–20] The 2s, 2p electrons of C, 2s, 2p electrons of N, 1s electrons of H, 5d, 6s, 6p electrons of Pb, 2s, 2p electrons of Sn, and the 5s, 5p electrons of I were explicitly treated as valence electrons.[22,23] In order to guarantee the accuracy of the calculation, the energy cutoff for plane-wave cut-off is 500 eV. We used an A (6× 6× 6) Monkhorst–Pack k-point grid for geometry optimization and an A (10× 10× 10) grid for calculating the density of states. For the best approach to this calculation, the generalized gradient approximation (GGA) approach which is accurate and the time saving was adopted instead of the local density approximation (LDA) and HSE approach. All considered structures were fully optimized with the force on each atom being less than 0.05 eV/Å.[21,22]

ABX3 type compound shows different phases under different temperatures. In the high temperature phase, the crystal structure of all ABX3 adopts a cubic perovskite structure as shown in Fig. 1. It is a three-dimensional framework of a corner-sharing BX6 octahedron in which the center is the radical group . All ABX3-type compounds studied in this paper are based on this cubic perovskite structure.

Structure of ABX3. X is shown in the vertex of the octahedron, B is shown in the center of the octabedron, the compound in the center is CH3NH3+.

The computations of optical properties were carried out by the perturbation theory method that was implemented in the VASP code. The main optical spectra, such as the refractive index N(ω), reflectivity R(ω), and adsorption coefficient I(ω), all can be obtained from the dynamical dielectric response functions (ɛ). The explicit expressions are given by

3. Results and discussion
3.1. Optical properties of ABX3

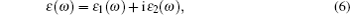
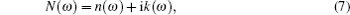
ABX3 compounds play a pivotal role in the perovskite sensitized solar cell mainly due to their optical properties which can induce the perovskite sensitized solar cells to absorb a wide range of light. According to Eqs. (1)–(5), it is clear that the wide absorptive capacities to different wavelengths of light on an absorber are the key factor in perovskite sensitized solar cells.

To find the material with the widest absorption range, the absorption coefficients of different ABX3 compounds were calculated. We tried both the GGA approach and the LDA approach, and their results are shown in Figs. 2 and 3 respectively. Both the methods reveal the same change trend of ABX3. Although the results from each of these two methods are not quite different from our optical calculation, the GGA method is used throughout our research because the GGA method can give a more accurate result than the experimental result through our calculating the electronic properties. As shown in Fig. 2, the absorption edge of ABX3 moves towards the lower energy side as the X component changes from Cl to Br, and to I progressively. For compounds containing Cl, the adsorption edge is close to 3.0 eV. For compounds with I, however, the edge changes into 1.5 eV. There is about 2.0 eV reduction on the optical gap for the substitution of I for Cl. Considering compounds with different B components, the substitution of Sn for Pb also reduces the optical gap moderately. According to the results, CH3NH3SnI3 has the smallest optical gap and thus can respond to the widest light spectra. Our calculations are consistent with experiments.[23]

Optical spectra of the absorption coefficient of ABX3 (A = CH3NH3; B = Sn, Pb; X = Cl, Br, I), obtained by the GGA method.

Optical spectra of the absorption coefficient of ABX3 (A = CH3NH3; B = Sn, Pb; X = Cl, Br, I) by the LDA method.

Optical spectra of CH3NH3SnI3. In panel (a), the black and red curves represent real and imaginary parts of dielectric function ɛ (ω), respectively. In panel (b) the black and red curves represent real and imaginary parts of refractive index, respectively. Panel (c) shows the optical spectrum of the reflectivity R. Panel (d) displays the optical spectrum of the absorption coefficient.

Figure 4 shows the detailed optical properties of CH3NH3SnI3, obtained by DFT calculations, which is in qualitative agreement with experimental observations.[23] For zero photon frequency, the imaginary part of the dielectric function is 0 while the static dielectric constant is 6.14. The imaginary part rapidly increases with increasing the frequency in a low energy region and has a peak at 2.42 eV. This peak results mainly from the transitions of I 5p and Sn 2s states to Sn 2p states. Using Eqs. (7)–(9), the complex refractive index spectra, the reflectivity, and absorption coefficient are obtained and the results are shown in Fig. 4. The complex refractive index (Fig. 4(b)) reveals a static refraction index of 2.47. The reflectivity R is shown in Fig. 4(c). When the photon energy is in a range of 0 eV–1.34 eV and k is close to zero, R is mainly influenced by static refractive index. The first peak of R is at 2.31 eV. We can find that the CH3NH3SnI3 has a relatively low reflectivity during ABX3, which makes CH3NH3SnI3 reflect less light. In Fig. 4(d), the optical spectrum of the absorption indicates comprehensive absorption information about CH3NH3SnI3, exhibiting the correlation between the absorption and the photon energy. The photon energy 1.34 eV is the threshold that determines whether CH3NH3SnI3 can absorb the photon energy. The optical spectrum of the absorption is caused by the radiative transitions of I 5p states and Sn 2s states to Sn 2p states. This energy belongs to all parts of visible light, thus CH3NH3SnI3 can absorb the wavelengths of light less than 925 nm. This range of wavelengths is much wider than that of light absorbed by other ABX3.

3.2. Electronic properties of ABX3

To understand the trend of absorption edges of various ABX3 compounds, their electronic properties must be addressed. According to the experimental data which we could find, the GGA method is more accurate than the LDA as shown in Fig. 5. We can see obviously that the results from the GGA method are always in better agreement with the experimental data that are shown in the blue line in Fig. 5 than those from the LDA method. In order to reduce the error of the calculation, the GGA approach, which is accurate, is adopted in our calculation.

According to the analysis of the density of states (DOS), electronic states near the band gap are governed by the orbital overlap of the BX6 octahedron. In detail, as shown in Fig. 6, the valence band maximum (VBM) is mainly composed of B cation p states, while the conduction band minimum (CBM) is dominated by X anion p states.[24] On the other hand, the CH3NH3 group makes little contribution to the band edges. As a result, the energy gap of ABX3 is determined by the cation B and anion X.[25–28]

Figure 7 shows the calculated band gaps of ABX3 compounds with various X and B components. For compounds with the same B component, the band gap decreases monotonically as the X components change from Cl to Br and to I. This is inconsistent with the decrease in the electronegativity for each of these three elements as listed in Table 1.[29] Partial substitution of a less electronegative component for the X component also results in the decrease of the band gap. Our results accord well with the experimental data as plotted in Fig. 7. On the other hand, for compounds with the same X component, the band gap increases with the decrease in the electronegativity of the cation element. The difference between the experimental results and the calculations is mainly caused by the influence of 3P0–3P2 spin–orbit splitting for Sn and Pb.

The band gaps and hence the optical edges of ABX3 compounds are governed by the electronegativity difference between the cation B and anion X. As the VBM is dominated by anion X components and the CBM is dominated by cation B, the separation between VBM and CBM is governed by the orbital interaction of the components. From a molecular theory point of view, the orbital interaction is closely related to the relative electronegativity between cation and anion. From this consideration, the results of the band gap shown in Fig. 7 can be understood.

The electronegativity difference between cation and anion also determines the bonding nature of the BX3 framework. As shown by the electron localization function (ELF) plotted in Fig. 8, as the X component changes from I to Br and to Cl, the bonding gets closer and closer to that of being ionic in nature. The substitution of Pb for Sn also results in a more ionic bonding.[30] For compounds studied here, CH3NH3SnI3 is composed of components that have a most small electronegativity difference. The BX3 framework of this compound is closest to being covalent. This compound also has a smallest band gap and can absorb the widest spectra of light.

Comparison of the band gaps of CH3NH3BX3 (B = Pb,Sn; X = Cl, Br, I), obtained by the LDA method (black line), and the GGA method (red line) with experimental results (blue line).

Density states of CH3NH3BX3 (B = Pb, Sn; X = Cl, Br, I).

Bandgaps corresponding to different matters of the ABX3.

The research on the relationship between the electronegativity and the optical and electronic properties of hybrid organic–inorganic perovskites could not only reveal the change regulation of ABX3 when the organic framework A is CH3NH3, but also provide a new way of explaining the basic physical efficiency-enhancing mechanism of all hybrid organic–inorganic perovskite structures ABX3.

Electronegativity by Pauling scale.

Element Electronegativity
Sn 1.96
Pb 1.8
Cl 3.16
Br 2.96
I 2.66

ELF map of CH3NH3BX3 compounds.

4. Conclusions

In this work, we systematically investigate the optical and electronic properties of ABX3 compounds through density functional calculations. For the ABX3 compounds studied, the absorption edge has a red-shift as the anion X changes from Cl to Br and to I and the cation changes from Pb to Sn when the organic framework A remains the same. As a result, CH3NH3SnI3 has the smallest optical gap and can respond to a very wide spectra of light. Our calculations of electronic properties of these compounds show that the fundamental band gap, consistent with the optical gap, is closely related to the cation and anion components. The variation of band gap with the component can be understood by the relative electronegativity between cation B and anion X when the organic framework A is unchanged. Our study not only highlights the important role of CH3NH3SnI3 for dye-sensitized solar cells, but also provides deep insight into the material engineering of ABX3 compounds.

Reference
1Lee M MTeuscher JMiyasaka TMurakami T NSnaith H J 2012 Science 338 643
2Burschka JPellet NMoon S JHumphry-Baker RGao PNazeeruddin M KGrätzel M 2013 Nature 499 316
3Heo J HIm S HNoh J HMandal T NLim C SChang J ALee Y HKim H JSarkar ANazeeruddin M K 2013 Nat. Photon. 7 486
4Stranks S DEperon G EGrancini GMenelaou CAlcocer M J PLeijtens THerz L MPetrozza ASnaith H J 2013 Science 342 341
5Memming R2001Semiconductor Electrochemistry2nd edn.GermanyWiley-VCHp. 358
6Kojima ATeshima KShirai YMiyasaka T 2009 J. Am. Chem. Soc. 10 1021
7Beiley Z MMcGehee M D2012Energy Environ. Sci.59173
8Jin HIm JFreeman A J 2012 Phys. Rev. B 86 121102
9Takahashi YObara RLin Z ZTakahashi YNaito TInabe TIshibashi STerakura K 2011 Dalton Trans. 40 5563
10Gratzel M2005Chemistry446841
11Kojima ATeshima KShirai YMiyasaka T 2009 J. Am. Chem. Soc. 131 6050
12Liu MJohnston M BSnaith H J 2013 Nature 501 323
13Hodes G 2013 Science 342 317
14Jiang Z QYao GAn X YFu Y JCao L HWu W DWang X M 2014 Chin. Phys. B 23 057104
15Yang Z JLiu J CCheng X LYang X DDai WLi JGuo Y D 2010 Chin. Phys. B 19 077102
16Kresse GFurthmuler J 1996 Phys. Rev. B 54 11169
17Kresse GFurthmuler J 1996 Comput. Mater. Sci. 6 15
18Perdew J PBurke KErnzerhof M 1996 Phys. Rev. Lett. 77 3865
19Anisimov VZaanen JAndersen O 1991 Phys. Rev. B 44 943
20Tanaka TMatsunaga KIkuhara Y 2003 Phys. Rev. B 68 205213
21Brivio FWalker A BWalsh A 2013 APL Materials 1 042111
22Frost J MButler K TBrivio FHendon C HSchilfgaarde M VWalsh A 2014 Nano Lett. 10 1021
23Hao FStoumpos C CCao D HRobert2014Nat. Photon.101038
24Wang YGould TimDobson J FZhang H MYang H GYao X DZhao H J 2014 Phys. Chem. Chem. Phys. 16 1424
25Mosconi EAmat ANazeeruddin M KGratzel MAngelis F D 2013 J. Phys. Chem. C 117 13902
26Wehrenfennig CLiu M ZSnaith H JJohnston M BHerz L M 2014 J. Phys. Chem. Lett. 5 1300
27Lang LYang J HLiu H RXiang H JGong X G 2014 Phys. Lett. A 378 290
28Brivio FButler K TWalsh ASchilfgaarde M V 2014 Phys. Rev. B 89 155204
29Lide D R2010CRC Handbook of Chemistry and Physics90th edn.The United States of AmericaCRCpp. 9–77
30Phillps J C 1970 Rev. Mod. Phys. 42 317