Semiconductors which have interesting electronic properties are used as important optoelectronic devices (laser diodes, detectors) and the progresses in the optoelectronic technology requires the development of new materials. III–V type semiconductor materials are relatively easy to synthesize, so these materials have been intensively studied by using theoretical and experimental methods. Especially, thallium-V compounds, which have been offered as important materials for long-wavelength infrared detectors^[1] and heterostructure field-effect transistors,^[2] have attracted considerable interest in recent years for electronic applications and optoelectronic devices. The theoretical^[1,3,4] and experimental works have provided the opportunity to study the growth, electronic and structural properties of thallium-V compounds. Improvements in the experimental procedures (MBE, MOVPE) have evoked the studies about the growth and electronic properties of thallium-V compounds and these systems have been performed many times in the early studies to investigate their structural stability.^[5]

Tl_xGa_1−xAs alloys were able to be synthesized^[6] and grown^[7,8] in the experimental investigations. Also these alloys have been examined in numerical studies.^[3,9] Zhou et al.^[9] have calculated the band structure and total energy of their electronic structure, by employing first principles calculations within density functional theory (DFT) and generalized gradient approximation (GGA). In their studies, they have examined 8-atom cubic unit cell Tl_nGa_4−nAs₄ and pronounced that the gap bowing of Tl_xGa_1−xAs shows a significant increase with the structural relaxation increasing, which is primarily attributed to the larger atomic size difference between Ga and Tl. Mankefors and Svensson^[3] also performed ab-initio calculations of the Ga_1−xTl_xAs alloys. It has been reported that the lattice constant and bulk modulus each had a positive dependence on the Tl concentration in the ternary system. The aim of the present study is to investigate bowing parameters and the origin of band gap bowing parameter in detail, and to study more thoroughly the electronic structures and bonding properties of these alloys.

It is expected that Tl–V compounds should have small or negative gaps due to the Tl band gap properties. Additionally, the combination of Tl with III–V compounds yields interesting new semiconductor ternary alloys. These new alloys show different characters from semiconductors to semi-metal compounds. Measurements and calculations of semiconductor alloys indicate that the band gap energy of the materials deviates from the behavior given by Vegard’s law.^[10] The addition of the second or higher order term is necessary for this deviation. This add-on term is known as the band-gap bowing parameter. This parameter determines the alloy band-gap energy and is a measure of the nonlinearity of the energy gap functional dependence on composition. For instance, we have reported a composition dependent bowing parameter for Ga_xTl_1−xP alloys^[11] in our previous study. For the Ga_xTl_1−xP alloys, the band gap increases with increasing the composition of Ga, even the compounds changing from metal to semiconducting phase.

The band gap bowing parameter is a crucial parameter to determine the alloy band-gap energies and it is a measure of the nonlinearity of the energy-gap functional dependence on composition. Experimental techniques (photoluminescence (PL), absorbtion) give different band gap values for the ternary alloys.^[12] To better understand the physical origins of the large dispersion and composition-dependent bowing in Tl_xGa_1−xAs alloys, we essentially investigate how the band gap bowing varies as a function of alloy composition. In the present study, we present a systematic and comparative study of the structural and electronic properties of the zincblende Tl_xGa_1−xAs (x = 0.125–0.875) alloys. Firstly, we compute the lattice constants and energy band gaps of the binary TlAs and GaAs compounds for the zincblende phase by using local density approximation (LDA) for exchange-correlation potential. Ternary compounds are constituted by means of a 16-atom supercell, and the composition dependence of lattice constants, density of states, energy band gap and physical origin of the band gap bowing parameter are represented.

In our study, the structural and electronic properties of TlAs and GaAs compounds and Tl_xGa_1−xAs alloys are investigated by using the plane wave pseudopotentials methods within the PWSCF software package^[13] which is based on DFT^[14,15] and pseudopotentials. Many DFT-based first-principles studies using plane wave ultrasoft pseudopotentials have been also performed in the early studies for different materials.^[16,17] Exchange and correlation potentials are described within the LDA. Wave functions are expanded in a plane wave basis to an 80-Ryd cutoff energy. Ga (4s²4p¹), As (4s²4p³), and Tl (5d¹06s²6p¹) valance electrons are used, and spin–orbit interactions are ignored throughout the calculations. Accurate Brillouin zone investigations are performed by the Monkhorst-Pack method with a 14 × 14 × 14 special k-point for binary compounds and 12 × 12 × 12 meshes for ternary alloys.

The Tl_xGa_1−xAs alloys with x = 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, and 0.875 are performed by using a 16-atom supercell in zincblende structure which corresponds to a 2 × 2 × 2 conventional cubic cell. In the calculations, firstly, the GaAs supercell is constituted and then Tl atoms are doped into this supercell to a desired concentration. Tl and As atoms are distributed randomly in the unit cells of Tl_xGa_1−xAs alloys. The different random distribution models of Tl and As atoms in the unit cell for a fixed value of x do not exhibit any change for structural nor electronic quantities of Tl_xGa_1−xAs alloys. All alloy configurations studied are relaxed by geometry optimization at their optimum volumes. All forces on the atoms are converged to less than 2.0 mRy/a.u., in the geometrical optimization.

We first examine the structural properties of the GaAs and TlAs zincblende phases which constitute the ternary alloys. The ground state structure of TlAs is determined as a zincblende phase in the early investigations.^[5] Lattice constants, bulk modulus, and gap energies of binary compounds are computed by fitting the calculated total energies with respect to different volumes to the Vinet’s equation^[18] of state (EOS). Results are given in Table 1 with the other theoretical and experimental results. In general, our results are in good agrement with previously reported ones. Especially, the lattice constants obtained for TlAs and GaAs are in reasonable agreement with the early theoretical studies.^[1,12,19] For GaAs, the computed lattice constant deviates from the experimental^[18] value within 1.85% and for TlAs, our lattice constant (6.169 Å) is very compatible to the one found earlier by van Schilfgaarde et al.^[1] (6.18 Å) and by Mazouz et al.^[19] (6.170 Å), however, the bandgap values which we obtained (−0.104 eV) are quite smaller than the values in Ref. [1] (with −2.12 eV) and Ref. [3] (with −1.86 eV). Table 1.

Values of lattice parameter a (Å), band gap energy (E_g), and bulk modulus (B₀) for the TlAs and GaAs in zincblende structure phase at equilibrium volume. Available pseudopotential data are also shown for comparison.

The band gap structures give the direct band gap Γ–Γ values of −0.104 eV and 1.354 eV for TlAs and GaAs, respectively. Band gap results are in general agreement with other theoretical calculations (Table 1) however, the calculated value of the energy gap of GaAs is underestimated by about 10.8% compared with the experimental value.^[20] We obtain a negative energy gap for TlAs, which exhibits a nearly semi-metallic character, but only in some theoretical studies^[5,21] has it been reported that no band gap exists in the TlAs. The obtained band structures of GaAs and TlAs binary alloys are plotted in Fig. 1. GaAs has a positive energy gap while TlAs shows a negative band gap due to inverted bands as found previously. From these band-gap graphs, we explain GaAs as a semiconductor material and TlAs as a semi-metalic one. Although LDA pseudopotential calculation underestimates the band gap energy, the band gap bowing parameters can be reliably calculated because only the relative values are important^[9] for these calculations. Fig. 1.

Band structures of zincblende GaAs and TlAs along the high symmetry directions in the Brillouin zone with LDA.

The lattice parameters, band gap energies and bulk modulus which we obtained for different concentrations of Tl in the Tl_xGa_1−xAs ternary alloys are listed in Table 2. According to these results, lattice constants increase with the increasing of thallium concentration and these ternary alloys show two different characters. The alloys of which the concentration ratios are x = 0.125 and x = 0.25 show semiconductor characters while the other alloys show semi-metallic characters. Table 2.

Calculated values of lattice parameter a (Å), band gap energy (E_g), and bulk modulus (B₀) for Tl_xGa_1−xAs ternary alloys in zincblende structure at equilibrium volume.

x	a/Å	Eg/eV	B0/GPa
0.00 GaAs	5.548	1.354	76.254
0.125	5.625	0.761	71.718
0.25	5.703	0.017	67.538
0.375	5.783	0.00	63.571
0.5	5.863	−0.026	60.179
0.625	5.939	−0.044	57.551
0.75	6.015	−0.145	55.237
0.875	6.092	−0.115	52.908
1 (TlAs)	6.169	−0.104	51.535

To proceed further with the analysis of the amount of deviation from the Vegard’s law, we compare the results in Fig. 2. In contrast to the computed lattice constants which are consistent with ones obtained from the Vegard’s law, the value of alloy bulk modulus deviates considerably from the linearity. In our calculations, we perform full geometry optimizations for supercell structures which are crucial for cell parameters. Fig. 2.

Composition dependences of the calculated lattice constant (a) and bulk modulus (b) of the ternary alloys compared with Vegard’s law predictions.

The lattice parameter data can be approximated by the following form:

where b is named the bowing or deviation parameter. We obtain a downward average bowing parameter (b = −0.006) by comparing the results. The obtained average deviation parameter is also compatible to the curves in Fig. 2. From the general aspect, it is observed that the lattice constant increases with the increasing of thallium concentration due to the bigger atomic radius of Tl than the atomic radius of gallium. The bulk modulus decreases with the increase of Tl concentration because of its relationship with the primitive unit cell volume . From the bulk modulus-Tl concentration curve in Fig. 2, we obtain an average bulk modulus deviation parameter of 14.139 GPA in a wider range of 0 < x < 1. We explain that the considerable difference between the bulk modulus of TlAs and GaAs gives rise to a large deviation parameter for the bulk modulus.

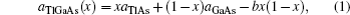
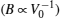
To determine the electronic properties of the system, we calculate the band structures of binary and ternary alloys along the high symmetry direction in the first Brillouin zone (BZ) for the calculated equilibrium lattice constant values. For some specific values of x, we plot the electronic band structures of the ternary alloys along the high symmetry points in BZ in Fig. 3. When the band structures are analyzed, we obtain materials with different characters. The Tl_xGa_1−xAs alloys with x = 0.125 and x = 0.25 show semiconductor characters with direct band gap values of 0.761 eV and 0.017 eV respectively, the other alloys (x > 0.25) behave as semimetal materials with the negative band gap values. The energy band gap decreases with the increase of Tl concentration and the gap disappears for the x = 0.375 value of ternary alloy. Above this value of x (x > 0.375), the band gap increases in the negative direction. These alloys are possible half-metal candidates which are metallic for one spin direction, while semiconducting for the other spin direction. These varieties of the band gaps of the materials make these materials applicable to wide areas such as the device production and spintronics application.^[22]

Figure 4 illustrates the DOSs of the ternary alloys (Tl_xGa_1−xAs) in zincblende structure at equilibrium volume for (a) x = 0.25, (b) x = 0.5, and (c) x = 0.75. The total density of states (TDOS) and partial density of states (PDOS) due to the constituent atoms are shown in their corresponding panels. Graphs focus on the near gap energy region to study the variation of band gap as a function of Tl content (x). The total and partial DOS obtained in this analysis confirm the above band structure results. Band gap energies are narrowed with the thallium content and a phase transition is observed above the x = 0.375 value. Fig. 3.

Electronic band structures along the high symmetry direction in the Brillouin zone for Tl_xGa_1−xAs alloys with (a) x = 0.25, (b) x = 0.5, and (c) x = 0.75. Valance band maximum is the zero energy level.

Fig. 4.

Total and partial DOS components calculated for Tl_xGa_1−xAs alloys in equilibrium volume with (a) x = 0.25, (b) x = 0.5, and (c) x = 0.75.

When the dos graphics are analyzed, it is generally observed that p-electrons of the Tl, Ga, and As atoms dominate in the valance and conduction bands. However, s orbitals of Tl and Ga atoms are only effective in the lowest group bands for the ternary alloys and there is a negligible effect of Tl-5d electrons on the studied ternary alloys. It is observed that As-4p states dominate the valance bands in all the samples. Additionally, as expected, the contributions of the thallium electrons to the valance band increase while the gallium electrons contributions decrease with increasing x concentration. In the conduction band, the contributions of Tl-4s and Tl-4p states increase while the contributions of Ga-4p states decrease and As contributions stay nearly stable with increasing Tl concentration. The crucial point which is observed in the band and dos graphs is that the conduction band width narrows with increasing x value and even disappears for large x-values.

The band gap energy of the ternary alloy can be depicted as a function of the band gap energy of the binary compound and determined with the following formula:^[23]

We calculate the band gap bowing parameter (b) of the ternary alloy by using this quadratic equation. We obtain an average band gap bowing parameter of nearly 4.48 eV for semiconducting phases (x = 0.125 and x = 0.25) and 2.412 eV for the semimetalic phases (x > 0.25).

The overall band gap bowing parameters of Tl_xGa_1−xAs alloys are also calculated from the equations of Bernard and Zunger^[24] for 0 < x < 1. In this approach, the overall bowing coefficient at a given average composition x measures the change in the band gap according to the formal reaction

where a_AC and a_BC are the equilibrium lattice constants of the binary compound and a_eq is the equilibrium lattice constant of the alloy with the average composition x. Equation (3) is decomposed into three steps:

Thus the band gap bowing parameters of the alloys are calculated as

Here, b_VD defines the relative response of the binaries to hydrostatique pressure from their individual equilibrium lattice constant to the alloy lattice constant value and b_CE describes the charge transfer effect due to the different bonding behaviors of the two binaries, b_SR measures the changes originating from structural relaxation in passing from the unrelaxed to the relaxed structure. These three terms are formulated as the following forms, with which we have also explained the origin of this equation in detail in our previous study:^[11]

All the energies (Eqs. (8)–(10)) are obtained via self consistent DOS calculations by using the above LDA scheme and the results are given in Table 3. The composition dependences of the calculated band gap bowing parameter (b_Zunger) together with the different contributions are shown in Fig. 5. Quadratic bowing parameter data are obtained by fitting the quadratic equation (Eq. (2)). In this fit, the energy gap values of the binary and ternary alloys are used. Fig. 5.

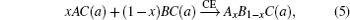
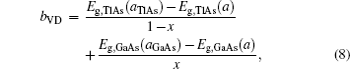
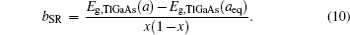
Composition dependences of calculated band gap bowing parameter b (a) and three contributions b_VD, b_CE, and b_SR (b).

Table 3.

Contributions of volume deformation, charge exchange, structural relaxation and formation energies of the ternary alloys are listed. Calculated band-gap bowing parameters (b_Zunger) of Tl_xGa_1−xAs ternary alloys are compared with that obtained by quadratic fit (b_Quad). All bowing parameters are in eV and formation energies are in Ry/f.u.

x	0.125	0.25	0.375	0.5	0.625	0.75	0.875
bVD	2.761	2.757	2.690	2.500	1.889	1.453	1.203
bCE	1.031	2.419	0.755	0.104	0.188	0.704	0.563
bSR	−0.036	0.011	0	0	0	0.005	0
bZunger	3.756	5.187	3.445	2.604	2.077	2.162	1.766
bQuad	3.771	5.189	3.449	2.604	2.081	2.154	1.771
Eform	−12.812	−18.098	−24.754	−28.674	−33.950	−39.225	−44.502

As seen from Table 3, both the total bowing parameters and all contributions (b_VD, b_CE, and b_SR) are strongly composition dependent and these parameters do not have an order depending on x values. The relatively large lattice mismatching between the binary compounds (10% for GaAs/TlAs) is very significant for the b_VD term and regarded as a strong composition dependent term. Also, the electronegativity difference between the atoms (Ga(1.81), Tl(1.62), and As(2.18)) and large discrepancy between covalent radii of the substitute atoms (Ga(1.22±0.03 Å) and Tl (1.45±0.07 Å)) contribute to such a strong composition dependence. The main contribution to the total gap bowing of all alloys come from the b_VD term and this term decreases with increasing the x value. The charge transfer effect (b_CE), which scales with the strong electronegativity mismatch between Tl and As, is also important for gap bowing of Tl_xGa_1−xAs alloys. Additionally, quadratic parameters which are obtained by the quadratic fit are consistent with parameters obtained from the Bernard–Zunger equations (Eqs. (7)–(10)). However, the results which are obtained from the two different ways are compatible.

Additionally, in order to study the stabilities of Tl_xGa_1−xAs alloys, we calculate the formation energies of all studied alloys (Table 3). The formation energy can give a measure of the stability of a material. So, we explain that the alloys are stable and these stabilities increase with increasing the Tl rate.

We also investigate the bonding properties of the ternary alloys to complete the basic background of the study. We analyze the charge density distributions to obtain an insight into the electronic natures of the alloys. The electronic charge density contours in the (110) crystallographic plane are shown for some special concentration values (x = 0.25, 0.5, and 0.75) in Fig. 6. The charge distributions each show a spherical concentration centered on Tl atoms and increasing thallium content does not affect the bonding character between the atoms. The charges around Ga atoms are uniformly distributed. Additionally, the charges accumulate nearer to the As along the bonds, since As atoms are more electronegative than Tl and Ga atoms. We also compute the electron charge density distribution in the (101) crystallographic plane for Tl_0.5Ga_0.5As ternary alloy to determine the anisotropy between any two planes in the crystal (Fig. 7). A comparison of the density distribution contour between (101) and (110) planes, indicates that this crystal is isotropic. Fig. 6.

Electronic charge density distribution contours calculated in the (110) crystallographic planes of Tl_xGa_1−xAs compounds with (a) x = 0.25, (b) x = 0.5, and (c) x = 0.75.

Fig. 7.

Electronic charge density distribution contour calculated in the (101) crystallographic planes of Tl_0.5Ga_0.5As compound.

Figure 8 shows the electron localization function for the Tl_0.5Ga_0.5As along the (101) plane. We also compute the valence-electron localization function (ELF) contour to determine the natures of bonding in the ternary alloys. The ELF function is normalized between 0 and 1 values that correspond to zero localization and strong localization, respectively and also the 0.5 value corresponds to free electron gas behavior. When the ELF distribution is analyzed, maximum ELF values are seen at Tl sites while Ga sites show small ELF values (Fig. 8). The positions of the corresponding atoms in Fig. 8 are the same as those in Fig. 7. Furthermore, it is seen that an ionic-type bonding appears between the Tl and As atoms because of a deep drop of ELF in the Tl–As bond region. However, along the Ga–As bond axis, a large region with high magnitude ELF is observed. This distribution shows a crucial character and a covalent bond between Ga and As atoms. Fig. 8.

Electronic localization function (ELF) contour calculated for the (101) crystallographic plane of Tl_0.5Ga_0.5As alloy.

We investigate the structural and electronic properties of TlAs, GaAs, and Tl_xGa_1−xAs alloys by utilizing numerical analysis based on first-principles calculations. We first determine that the structural and electronic properties of the binary compounds are in good agreement with available theoretical and experimental results. To investigate the structural and electronic properties of zincblende Tl_xGa_1−xAs alloys, we calculate the band-structure, lattice parameter, electronic density of states, charge density graphs and gap bowing parameter. It is found that the relaxed lattice constants of the ternary alloys are very compatible with the calculations from Vegard’s law and a small downward bowing parameter equal to 0.006 Å is obtained. However, we obtain a large upward bulk modulus bowing parameter equal to 14.139 GPa because of the distinctive difference in bulk modulus between the GaAs and TlAs. The band gap energies are obtained for various alloy compositions through the electronic band-structure calculations, and it is observed that Tl_xGa_1−xAs alloys have a semiconductor character for x = 0.125 and x = 0.25 concentration values and semi-metalic character for other concentration values. We find that the ternary Tl_xGa_1−xAs alloys each have an average band gap bowing parameter of 4.48 eV for semiconductor ones and 2.412 eV for semimetals.

Substitution of thallium for GaAs changes the materials from the semiconductor phase to the semimetalic phase and leads to a large and composition dependent band-gap bowing parameter. According to this important effect, our study can be useful for enhancing the performances of the optoelectronic devices and for further studies.