† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Kulwinder Kaur thanks Council of Scientific & Industrial Research (CSIR), India for providing fellowship.
In this paper, electronic and thermoelectric properties of Mg2C are investigated by using first principle pseudo potential method based on density functional theory and Boltzmann transport equations. We calculate the lattice parameters, bulk modulus, band gap and thermoelectric properties (Seebeck coefficient, electrical conductivity, and thermal conductivity) of this material at different temperatures and compare them with available experimental and other theoretical data. The calculations show that Mg2C is indirect band semiconductor with a band gap of 0.75 eV. The negative value of Seebeck coefficient shows that the conduction is due to electrons. The electrical conductivity decreases with temperature and Power factor (PF) increases with temperature. The thermoelectric properties of Mg2C have been calculated in a temperature range of 100 K–1200 K.
Thermoelectric materials and their applications provide an option of improving the sustainability of electricity which is generated from the waste heat by means of thermoelectric generators that convert heat energy directly into electricity and offer many benefits like moderate efficiency, simple device structure and no moving parts. Thermoelectric-based generators and refrigerators are solid state devices in which heat energy is converted into electricity and vice versa. Thermoelectric generators have been used in niche applications such as power generation or remote power sources.[1] Thermoelectric refrigerator is environment friendly and has long life, and potential to replace traditional air conditioner. Semiconducting alkaline earth metal compounds have been of immense interest for use in thermoelectric device applications.[2,3] One important parameter, which evaluates the performance of thermoelectric material, is a dimensionless figure of merit ZT,[4] which is defined as


Good thermoelectric material has high thermo power and low thermal conductivity. High performance thermoelectric material is usually considered to have ZT equal to or greater than one. Magnesium compounds Mg2X (X = Si, Ge, Sn) and their solid solutions are of great interest as promising thermoelectric materials in a temperature range from 500 K to 900 K. These materials are semiconductors having antifluorite structure. The antifluorite semiconductor is important because it forms metal-semiconductor hybrid material.[6] Mg2Si and Mg2Ge are good materials for technological applications as infrared detectors in a wavelength range of 1.2 μm–1.8 μm for optical fiber.[7] Carbides, which have been intensively studied for more than half a century, still remain a major center of scientific and technological attention.[8] Magnesium compounds containing Mg–C and C–C bonds are quite fascinating from both fundamental science and synthesis perspectives.[9,10] The carbon has two Mg–C bonds and a lone pair. The two magnesium atoms are bonded by single Mg–Mg bond. The carbon center is much like an organic carbene. The nature of chemical bond presents and determines the properties of Mg2C. There is no covalent C–C bond in Mg2C. So these types of materials are ionic semiconductors.[11] sp3 and sp2 carbon network are intercalated with Mg[12,13] and novel polymeric carbide.[10] The nature of Mg–C chemical bond has great importance in polar organometallic compounds and in the covalent /ionic nature of carbanions.[14,15] There are four magnesium carbides, which are well known as (i) tetragonal MgC2, (ii) orthorhombic α-Mg2C3, (iii) monoclinic β-Mg2C3, and (iv) cubic Mg2C. In the present paper, we will discuss the electronic and thermoelectric properties of cubic Mg2C because this phase exists at high temperature and pressure. It was theoretically investigated by Cork ill and Cohen[11] in 1993. And recently synthesized by Kurakevych et al.[16] at high pressure conditions, this compound forms from the elements at pressure above 15 GPa and stable in ambient Fm3m conditions. Owing to small size of C atom, it has large elastic modulus, which is related to hardness. This material is good for high temperature and pressure applications.[9] This compound is unique in the sense that carbon is stabilized in a rare C4– ionic state, which is extremely rare for alkaline–earth metal carbides.[16] Carbon is eight fold coordinated by magnesium, and magnesium has four fold coordinated with carbon. This compound is easily hydrolyzed by the moisture in air, so it must be handled carefully. Li et al.[17] have investigated the electronic and lattice vibrational properties of Mg2C by the pseudo potential method. They found that this compound is small gap semiconductor. Laref et al.[18] reported the mechanical, electronic and optical properties of this compound. Recent study by Chernatynskiy and Phillpot[19] revealed that the calculated thermal conductivity is 34 W/mK for Mg2C at 300 °C. Theoretical and experimental studies of thermoelectric properties for Mg2C system are not yet available in the literature. These calculations may serve as the guidance for researchers in future. The aim of the present work is to investigate the electronic properties by using density functional theory and thermoelectric properties by using phonon Boltzmann transport equation (pBTE) and Boltzmann transport equations.
Mg2C is face centered cubic (FCC) structures with primitive translation vectors 
The present calculations were performed using density functional theory (DFT) with the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA)[21] and using plane wave pseudo potential method as implemented in Quantum Espresso package.[22] Norm-conserving pseudo potential based on the Troullier–Martins scheme were utilized to model core electrons. The cutoff for the kinetic energy was set to be 70 Ry (1 Ry = 13.6056923 eV) for the plane-wave expansion of the electronic wave function. The marzari-Vanderbilt smearing size was fixed to be 0.003 Ry. The internal lattice pressure was smaller than 0.2 kbar (1 bar = 105 Pa). The Brillouin zone integration was performed over a Monkhorst–Pack[23] 5 × 10 × 10 meshes. The lattice constant of Mg2C was optimized until the total energy converged to at least 10−8 Ry, the forces between atoms became smaller than 10−5 Ry/bohr. A denser k-mesh of 16 × 16 × 16 was used for calculating the density of states. A very fine mesh of 58 × 58 × 58 points was used to determine the final electronic structure for use in the electronic thermoelectric properties calculations. BoltzTraP code[24] was used to find the electronic thermoelectric properties (Seebeck coefficient (S), electrical conductivity (σ), and electronic thermal conductivity (ke), which is based on constant time approximation and rigid band approximation [RBA].[25,26] To calculate transport properties, the following Boltzmann semi classic equations are used



In RBA approximation the band structure remains unchanged as the Fermi level is moved up and down. Shifting the Fermi level only results in changes of electron and hole concentrations because the donor and acceptor doping levels are varied. With this code, the thermoelectric properties were calculated with respect to the relaxation time (τ). To calculate lattice thermal conductivity (kl), ShengBTE code[27] based on the phonon Boltzmann transport equation (pBTE) was used. This code is based on the second-order (harmonic) and third-order (an harmonic) interatomic force constants (IFCs) combined with a full solution of the pBTE and successfully predicts the lattice thermal conductivity (kl).[28,29] The lattice parameter and bulk modulus were calculated by computing the total energy for different volumes and fitted to Murnaghan’s equation of state:[30]


Our calculated lattice constant of Mg2C is 5.443 Å, which is in better agreement with experimental data reported by Kurakevych et al.[16] as compared with the previously reported theoretical data by Kalarasse and Bennecer.[31] Comparisons among other reported theoretical and experimental data of calculated lattice constant, bulk modulus, band gap have shown in Table
| Table 1. Lattice constants, band gaps and bulk moduli of Mg2C. . |
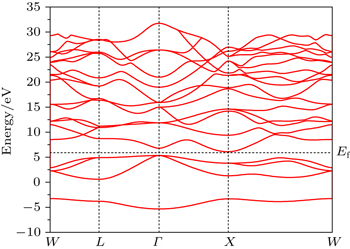
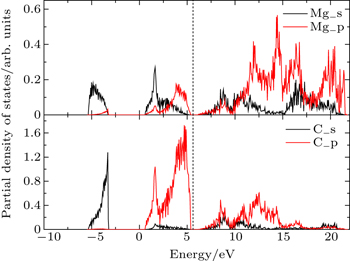
Figure
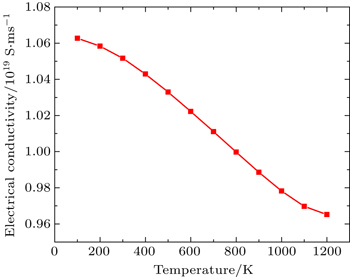
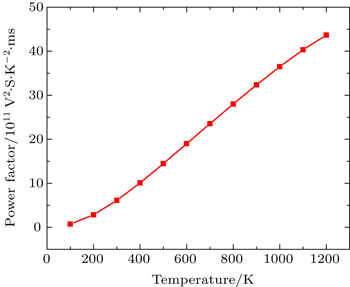
In this Subsection, thermoelectric properties are presented. Figure

Figure

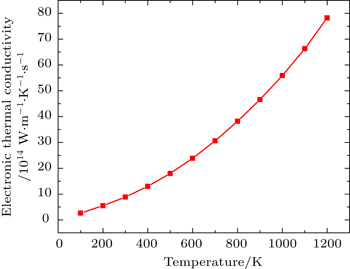
Total thermal conductivity is sum of electronic (ke) and lattice part (kl) of crystal as given by

Figure
By using first principle calculations, the electronic and thermoelectric properties of pure Mg2C are investigated. The calculated result shows that Mg2C exhibits the n-type conduction, i.e., the conduction is due to electrons, and also it is confirmed that Mg2C is an indirect semiconductor. Thermoelectric studies show that Seebeck coefficient increases with increasing temperature. The electrical conductivity decreases with increasing temperature due to change of mobility. The electronic part of thermal conductivity (ke) increases with increasing temperature and lattice contribution decreases with increasing temperature. The calculated result proves that the figure of merit (ZT) is very low.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 |