Cite this Article
Zhang Yong-Liang, Feng Fan, Liu Fu-Cheng, Dong Li-Fang, He Ya-Feng. Cycloid motions of grains in a dust plasma. Chinese Physics B, 2016, 25(2): 025201  
Permissions
Cycloid motions of grains in a dust plasma
Zhang Yong-Liang, Feng Fan, Liu Fu-Cheng, Dong Li-Fang, He Ya-Feng†,
Hebei Key Laboratory of Optic-electronic Information Materials, College of Physics Science and Technology, Hebei University, Baoding 071002, China

 

† Corresponding author. E-mail: Heyf@hbu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11205044 and 11405042), the Natural Science Foundation of Hebei Province, China (Grant Nos. A2011201006 and A2012201015), the Research Foundation of Education Bureau of Hebei Province, China (Grant No. Y2012009), the Program for Young Principal Investigators of Hebei Province, and the Midwest Universities Comprehensive Strength Promotion Project.

Abstract
Abstract

Hypocycloid and epicycloid motions of irregular grains (pine pollen) are observed for the first time in a dust plasma in a two-dimensional (2D) horizontal plane. These cycloid motions can be regarded as a combination of a primary circle and a secondary circle. An inverse Magnus force originating from the spin of the irregular grain gives rise to the primary circle. Radial confinement resulting from the electrostatic force and the ion drag force, together with inverse Magnus force, plays an important role in the formation of the secondary circle. In addition, the cyclotron radius is seen to change periodically during the cycloid motion. Force analysis and comparison experiments have shown that the cycloid motions are distinctive features of an irregular grain immersed in a plasma.

PACS: 52.27.Lw;52.40.Kh;52.90.+z
Keyword:dust plasma;irregular grain;cycloid motions
1. Introduction

The dust plasma is characterized by charged grains immersed in a plasma of electrons and ions.[1–3] The grains could acquire charges of the order of 103 to 104 elementary charges and often become strongly coupled, which gives rise to novel phenomena such as the crystallization, phase transitions, and waves.[4–9] The grains suspended in sheath suffer gravitation force, electrostatic force, drag force, and sometime external magnetic/laser field etc. It leads to complex motions of grains like gyromotion, cluster rotation and shear flow.[10–17] It is obvious that a charged grain could perform gyromotion if it is magnetized in external magnetic field. The measurements of gyroradius and cyclotron frequency provide an effective method for the noninvasive determination of the charge on a grain.

Most of studies on the dust plasma either in experiment or in theory deal with grain of a spherical form, such as the glass, melamine formaldehyde, and alumina mocrosphere.[3–5] In some cases, especially in the numerical simulation of molecular dynamics, for simplicity, the grain is considered as a charged particle neglecting the grain shape. However, the grains appeared in planetary rings, fusion reactors, materials processing, etc., generally have a nonspherical shape. The dynamics of the nonspherical grain in the dust plasma is less known at present.

A grain immersed in a plasma suffers the momenta transferred from plasma flux and surrounding gas.[1–3] This could result in the spin of the grain and has been paid much attention in recent years.[18–20] For an ideal spherical grain, the net effect for the momenta transfer can be zero. For a grain with irregular shape the net transfer of the angular momenta can be estimated as ηassπ a2ni,∞miavsv∞[18] (where ηass is the coefficient taking into account the degree of irregularity of the dust shape, a is the average radius of the grain, ni,∞ is the ion density, mi is the ion mass, vs is the ion velocity at the surface of the grain when they are attached to the grain and v∞ is the ion velocity far from the grain). The angular frequency of such spin can reach a rather large value (∼104 s−1–109 s−1).[19] The spin of a hollow glass microsphere with defect has been detected with angular velocity up to 12000 rad/s in a stratified glow discharge.[19] The spin of a charged grain could give rise to a magnetic moment. Interacting with external magnetic field, the spinning grain is subjected to a magnetic force which could result in the complex motions of such grain.[18,21] However, in the absent of external magnetic field, a spinning grain could also exhibit complex motions which have not been well studied until now. Here, we report an experimental study on the cycloid motions of irregular grains (pine pollen) in a dusty plasma. Hypocycloid and epicycloid motions are observed, besides the stationary grain and the circle motion of grain. The inverse Magnus force originated from the spin of the grain is considered, and it plays important role on the cycloid motions of grains. These complex motions of grains are explained based on the force analysis in 2D horizontal plane. Additional comparison experiments with regular microspheres are performed in order to confirmed that the cycloid motions are distinctive features of a pine pollen immersed in a plasma.

2. Experimental setup

Figure 1 shows the sketch of the experimental apparatus. The experiments are carried out in a vacuum chamber with a background pressure within p = 10–70 Pa. Argon gas at flow of 10 sccm is used for the discharge. In order to avoid disturbances in grain motion during an experiment the position of the gas inlet is designed properly. Plasma is produced by coupling capacitively the electrode to a radio-frequency generator (13.56 MHz). The forward power varies from 5 W to 50 W. The separation between the lower stainless steel electrode and the upper ITO coated electrode is 70 mm. Due to the lack of probe, the plasma parameters are obtained by using numerical simulations with a two-dimensional fluid model based on the continuity equations for mass, momentum and electron energy, and Poisson equation for the electric field.[22] The electron density is ne = 1.8×1010 cm−3 and the electron temperature is Te = 2.2 eV under the given experimental conditions, which are in agreement with the experimental results by Basner.[23]

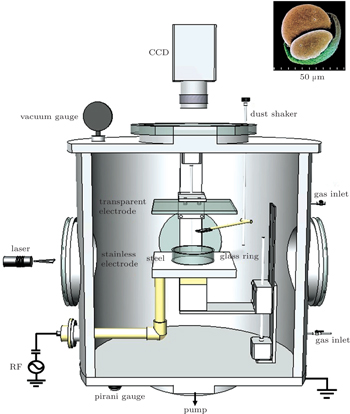Fig. 1. Schematic diagram of the experimental setup. The inset shows the image of a pine pollen we used in experiments.

Pine pollen having nonspherical shape as shown by the inset in Fig. 1 are injected into the plasma through a shaker and serve as dust grains. The average radius is about (20±5) μm. The charge Q of a dust grain can be obtained by means of the methods of force balance and/or resonance frequency,[24] Q ≃ 5 × 104e. One or few grains are injected into the plasma during each experiment in order to avoid the formation of grain ring and plasma condensation. Regular glass and resin microspheres are also used in comparison experiments. Grain is horizontally illuminated by a 50-mW, 532-nm laser sheet with a thickness of 0.5 mm and imaged by a CCD camera from the upper transparent electrode. The spatial and temporal resolutions are 10 μm/pixel and 50 frames/s, respectively. The trajectory of grain can be obtained by using long-time exposure. In order to obtain the velocity and acceleration of grain a high speed camera (PCO.dimax, 1000 fps) is used. Characteristic parameters of the grain movement are measured by using the image processing with MATLAB.

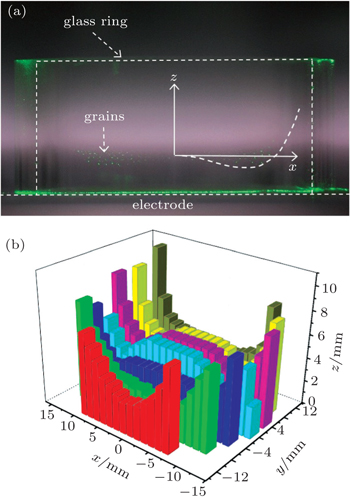
A glass ring is positioned on the lower stainless steel electrode. The diameter and the height of the glass ring are 37 mm and 10 mm, respectively. After being injected into the plasma, charged grain levitates nearby the glass wall. Due to the circular symmetry of the glass ring the grain travels around the glass ring or stays near its equilibrium position.

3. Experimental results
3.1. Regular movements of grains

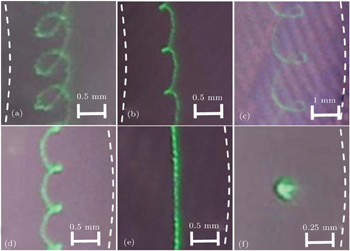
We firstly show the regular movement of a single grain around the glass ring in a 2D horizontal plane as shown in Fig. 2. Figure 2(a) shows an epicycloid motion with inward petals. This meandering motion can be regarded as a combination of two circular motions, where the primary circle (radius r2) orbits the secondary circle (radius r1) in one direction with angular velocity ω1 and spins about its center in the same direction with angular velocity ω2 as shown by the diagram of Fig. 3(a). Figure 2(c) shows a hypocycloid motion with outward petals with rotations in the opposite sense [as illustrated by the diagram of Fig. 3(b)]. The epicycloid and hypocycloid motions occur in two cases, respectively. The epicycloid trajectory is observed only outside of the glass ring, and the value of angular velocity satisfies ω1ω2 > 0. The hypocycloid trajectory is found both inside and outside the glass ring, and the value of angular velocity satisfies ω1ω2 < 0. For the two kinds of cycloid motions they both satisfy the following relation:

i.e., the linear speed of the secondary circle is less than that of the primary circle. This is a key to the formations of the petals on both epicycloid and hypocycloid trajectories.

Fig. 2. Trajectories of travelling (a)–(e) and stationary (f) grains. Dashed line in each image indicates schematically the glass ring. Panels (a) and (b) are located outside the glass ring. Panels (c)–(f) are located inside the glass ring. (a): epicycloid motion; (b): cuspate epicycloid motion; (c): hypocycloid motion; (d): cuspate hypocycloid motion; (e): circular motion; (f): stationary grain. Exposure times of panels (a)–(f) are: 0.39, 0.26, 0.53, 0.16, 0.32, 1 s, respectively.

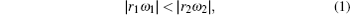
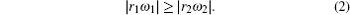
Cuspate epicycloid and hypocycloid motions are observed as shown in Fig. 2(b) and 2(d), respectively. In these cases, the radius r1,2 and the angular velocity ω1,2 follow the condition:

This means that the linear speed of the secondary circle is equal or greater than that of the primary circle, which leads to the appearance of the cusps on the cuspate cycloid trajectories. The cuspate epicycloid motion is observed only outside the glass ring, and the value of angular velocity satisfies ω1ω2 > 0. The cuspate hypocycloid motion is observed both inside and outside the glass ring, and the value of angular velocity satisfies ω1ω2 < 0.

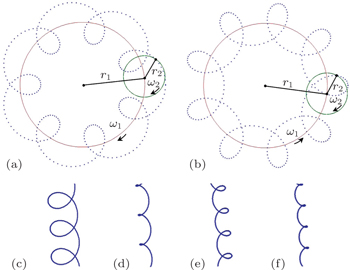
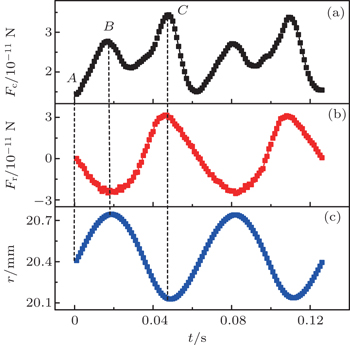
Circular motion is observed both inside and outside the glass ring as shown in Fig. 2(e). The angular speed of circular motion of grain changes within the range of 0.05 rad/s–1.23 rad/s. Stationary grain is observed both inside and outside the glass ring as shown in Fig. 2(f). In the absent of action with other grain, the grain is considerably stable at higher gas pressure. However, Brownian motion of grain is observed clearly at lower gas pressure. The grain moves stochastically near its equilibrium position. This has also been reported by other groups.[25]

Which trajectory a grain will follow is determined by the initial conditions (such as the initial position and the angular velocity) of the dropped grain and the discharge parameters. This means that for several grains dropped simultaneously (or one grain dropped repeatedly), they (it) will exhibit different trajectories because their (its) initial conditions are not exactly the same. Therefore, the dependencies of the parameters r1,2 and ω1,2 mentioned above on the gas pressure and the forward power of discharge could not be illustrated evidently. In our experiments, the radii of the primary and the secondary circles change within the ranges of r2 = 0.08 mm–0.57 mm and r1 = 13 mm–25 mm, respectively. The corresponding values of angular velocities change within the ranges of ω2 = 24 rad/s–88 rad/s and ω1 = 0.03 rad/s–0.63 rad/s, respectively.

Fig. 3. Schematic diagram of cycloid motions. (a): epicycloid; (b): hypocycloid. Dotted line represents the trajectory of cycloid motions of grains. Solid line and dashed line indicate the primary circle and the secondary circle, respectively. r2 and r1 represent the radii of the primary and the secondary circles, respectively. ω2 and ω1 represent the angular velocities of the primary and the secondary circles, respectively. Panels (a) and (b) occur when ω1ω2 > 0 and ω1ω2 < 0, respectively. Panels (c)–(f) reproduce the trajectories as shown in Figs. 2(a)–2(d) in term of Eqs. (1)–(4). The parameters are ω1 = 0.14, 0.15, 0.42, 0.22 rad/s, ω2 = 44.52, 27.45, −45.13, −32.63 rad/s, r1 = 20.39, 20.27, 12.31, 13.17 mm, r2 = 0.21, 0.14, 0.25, 0.12 mm in Figs. 2(a)–2(d) and Figs. 3(c)–3(f), respectively.

The (cuspate) cycloid motions of grains follow the parameter equations in polar coordinate if we pick the center of glass ring as the origin:

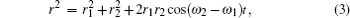
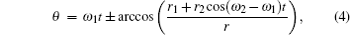
where, “+” and “−” correspond the cases of sin(ω2−ω1)t > 0 and sin(ω2−ω1)t ≤ 0, respectively. r and θ represent the radial and azimuth positions of grains in polar coordinate, respectively. ωi and ri (i = 1,2) are defined as above. By using the measured ω1, ω2, r1, r2 in Fig. 2(a)–2(d), we can reproduce the observed cycloid motions in term of Eqs. (1)–(4) as shown in Fig. 3(c)–3(f). Due to the pressure on the grain from the horizontal laser, there are some distortions on the experimental cycloid trajectories [Fig. 2(a)–2(d)] as compared with Fig. 3(c)–3(f).

3.2. Force analysis

The force analysis for a nonspherical grain, like the pine pollen we used, becomes very complex. These forces mainly include the gravitation force, electrostatic force, ion drag force, neutral friction force, and inverse Magnus force. The inverse Magnus force, which originates from the spin of a nonspherical grain, is considered here for the first time. The interaction force between grains is not considered in the present case because only one or few grains separated well are dropped in each experiment.

The gravitation force Fg = mg acts downward vertically and will not be considered here because our emphases is on the horizontal motions of dust grains.

Fig. 4. Sheath profile indicated by the grain distribution in x–z plane at y = 0 mm (a) and in three-dimensional (3D) space (b). Radial profile of the sheath inside the glass ring is indicated by the dropped grains illuminated by a vertical laser sheet. Gas pressure is 15 Pa and forward power is 8 W.

The electrostatic force originates from the action of sheath field on the negatively-charged grain. In the present of a glass ring the sheath profile follows approximately the walls of the glass ring and the electrode. Because the thickness of sheath near the glass ring and the electrode are different,[26] the confinement of the sheath to the grain becomes complex. When the diameter of the glass ring is small, the horizontal confinement to the grain could be described by a parabolic potential, and the grain is confined to the center of the glass ring.[3] Here, the glass ring is relatively large, and the grain is restricted near the glass wall both inside and outside. In order to obtain the radial distribution of the sheath, we drop plenty of grains into the glass ring and capture the grain distribution in x–z plane illuminated by a vertical laser sheet as shown in Fig. 4(a). The sheath profile inside the glass ring can be obtained approximatively by fitting the bottom profile of grain distribution by superposing 20 images as indicated by the dashed line in Fig. 4(a). If we pick the center of glass ring as the origin of polar coordinate, the radially confining potential is fitted approximately by a quartic polynomial:

here, r represents the radial distance to the center of the glass ring. For the sake of simplicity, the radial confinement outside the glass ring has a mirror symmetry about the glass wall as shown by the solid lines in Fig. 6(a). Furthermore, by means of a measurement of spatial resolution in y direction, we can obtain the 3D sheath profile as shown in Fig. 4(b). It can be seen that the sheath near the glass wall is lower than that in the center of the glass ring, which gives rise to the confining potential to the grain. Beyond the minima of the confining potential as indicated by the dashed line in Fig. 6(a), the grain is attracted toward the center of the glass ring. On the contrary, within the minima of the confining potential, the grain is repulsed toward the glass wall. The present of the potential well plays important role to the formation of the cycloid motions of grains.

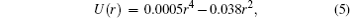
Ion drag force acting on the grain by ion flow results mainly from Coulomb drag and collection drag, and has been explored extensively. Together with the neutral drag and the plasma charging flux, the ion drag could give rise to the spin of the immersed grain. The spin of a hollow transparent glass microsphere with surface defect was observed in a stratified glow discharge by Karasev et al.[19] The values of angular velocity measured in their experiments are between 0 and 12000 rad/s. As a rule, for the nonspherical grain as we used here, the pine pollen would spin faster than the glass microsphere they used because the surface of pine pollen is much irregular than that of glass microsphere. The rapid spin of the pine pollen around its center of inertia gives rise to the inverse Magnus force which plays important role on the complex motions of grains.

The inverse Magnus force results from the spin of a travelling grain in rarefied fluid as illustrated by Fig. 5. As is well known, the normal Magnus force usually occurs in dense fluid (the Knudsen number Kn = λ/d is negligibly small, here, λ is the mean free path of the fluid, d is the diameter of the grain) and can be described by using the Navier–Stokes equations,[27] which has depicted well the arc trajectory of “banana kick”. However, in rarefied fluid (for Kn ≫ 1), the inverse Magnus force occurs and can be described in term of the method of free molecular flow[28]

here, ω0 and v represent the vectors of angular velocity and travelling velocity of a spinning grain, respectively. η is the density of fluid. k is a coefficient related with the shape of the grain. The minus sign in Eq. (6) represents the inverse Magnus effect. In our experiment, the mean free path of neutral gas is λ∼0.7 mm (P = 10 Pa), the diameter of grain is d ∼ 40 μm, and the Knudsen number is Kn ≫ 1. Therefore, the description of fluid dynamical limit is not applicable in this case. Because the inverse Magnus force acts perpendicularly to the travelling direction of the grain, it could provide the centripetal force for the cycloid motion of the grain travelling along the primary circle. Here, we focus on the case that the vector of angular velocity of the spinning grain is along the vertical direction, i.e., the inverse Magnus force acting on the grain is always along the horizontal plane.

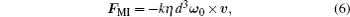
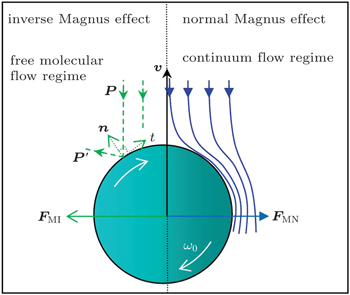Fig. 5. Schematic diagram of the inverse (normal) Magnus force FMI (FMN) acting on a spinning grain. In the free molecular flow regime, P (P′) represents the pre-impact momentum (deflected momentum).

The neutral drag force is a resistance force caused by the collisions with the neutral gas molecules. It damps the motion of grain. Therefore a driving force is necessary for the grain to keep moving forward along the orbit. Although the origin of this unknown driving force is still unclear at present, we can give some suggestions. 1) It should be related with the irregularity of the grain, because our comparison experiments with glass and resin microspheres have shown that no cycloid motion and no circle motion are observed. Several groups also reported the rotation of nonspherical agglomerate of microspheres. The rotation of microsphere is observed only in a magnetized dust plasma, which is induced by the Lorentz force.[6,13] 2) This driving force is nondirectional with regard to the glass ring because both clockwise and counterclockwise rotations are observed. 3) It should be the same order of magnitude of the neutral drag force because the grain could continue to move uniformly along the glass ring. In the following we will neglect the counteractive neutral drag force and driving force.

3.3. Origin of the primary circle

The cycloid motion of the grain is characteristic of a combination of the primary and the secondary circles. Therefore, the essential origins of the primary and the secondary circles are keys to understand the formations of these cycloid motions.

For a charged grain travelling along the primary circle in a plasma, a persistently centripetal force is required. As is well known, the Lorentz force and the inverse Magnus force are characteristic of their transverse action with respect to the travelling direction of an object. However, no magnetic field is applied to the charged grain in our experiments. Therefore, only the inverse Magnus force appears and provides the persistently centripetal force for the rotation of the grain along the primary circle. Other forces mentioned above cannot provide persistently centripetal action on the travelling grain. For example the horizontal components of the electrostatic force and ion drag force act only in radial direction due to the rotational symmetry of the glass ring. Although those forces are not the origin of the primary circle, they play important role in the formation of the secondary circle.

The spin of the irregular charged grain is the key to the cycloid motion via inverse Magnus effect. In order to confirm these distinctive features of the cycloid motions the pine pollen has exhibited as shown above, further experiments with glass and resin microspheres are performed at the same discharge conditions for comparison (not shown here). No cycloid motion is observed. Those regular microspheres (less spin) show behaviours such as the random motion and the crystallization as other groups observed previously. Therefore, we can draw a conclusion that the spin of the pine pollen gives rise to the inverse Magnus force which provides the centripetal force for the primary circle.

3.4. Origin of the secondary circle

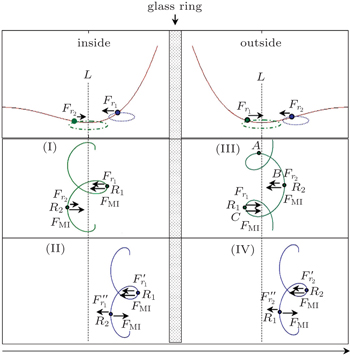
Our observations of the cycloid motions of grains can be classified roughly into four groups (I)–(IV) as shown by the diagrams in Fig. 6(b). The equilibrium line L indicates the position of minimum of the radially confining potential.

Fig. 6. Schematic diagram of the grain trajectories. Solid lines in panel (a) illustrate the approximate profile of sheath in vertical section. Equilibrium line L (dashed line) indicates the position of the minima value of confining potential. F1 represents the horizontal component of the radially confining force when the grain is between the equilibrium line L and the glass wall. Outside this region, it is expressed as F2. Panel (b) shows four cases of complex trajectories in a horizontal plane. (I), (II), and (IV) show the hypocycloid motions, and (III) shows the epicycloid motion. FMI represents the inverse Magnus force. R1 (R2) is the cyclotron radius when the grain is near (far away from) the glass wall.

For the case (III), the grain meanders near the equilibrium line L. The centripetal forces at points B and C read:

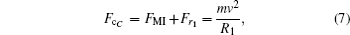
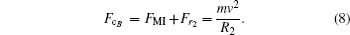
Here, Fr1 is slightly larger than Fr2 due to the steep sheath near the glass wall, therefore the cyclotron radii R1 < R2. The periodical change of the cyclotron radius as the grain travelling gives rise to the epicycloid trajectory as illustrated by Fig. 2(a).

The centripetal force Fc consists of inverse Magnus force FMI and radial confinement force Fr as shown by Eqs. (7) and (8). Fc = mv2/r and Fr = mar can be obtained experimentally from the grain trajectory with high speed camera at the frame of 1000 fps. Figure 7(a) shows the dependance of the centripetal force Fc on the time within two cycles. It can be seen that the centripetal force at point C (case III in Fig. 6) is FcC = 3.4×10−11 N, the centripetal force at point B is FcB = 2.7×10−11 N, FcC > FcB. Obviously, the magnitude of radially confining forces Fr at points B and C are in accord with Fc as shown in Fig. 7(b), i.e., |FrC| > |FrB|. Near the equilibrium line L, as indicated by point A in Fig. 6(b) III, the radial confinement disappears, Fr = 0, as shown in Fig. 7(b). In this case, only inverse Magnus force plays the role of centripetal force, i.e., FcA = FMI. Therefore, we can obtain the inverse Magnus force FMI = FcA = 1.44×10−11 N. In Eq. (6), η∼9×10−4 kg/m3 at 50 Pa, d∼40 μm, and v∼0.04 m/s obtained from the trajectory, then we have kω0 ≃ mω2/η d3 ≃ 5×106 rad/s. Here, if we suppose k ≃ 5π for the pine pollen, which is five times than that for a microsphere, the value of the angular velocity of spin is about ω0 ≃ 3×105 rad/s. This value is reasonably larger than that observed by Karasev et al. (1.2×104 rad/s) because the pine pollen we used is more irregular than the hollow transparent glass microsphere they used. However, experimental detection of such a grain spinning faster is out of the reach of our camera at present.

Fig. 7. Dependance of the centripetal force Fc = mv2/r (a), the radially confining force Fr = mar (m: grain mass, ar: radial acceleration) (b), and the radial position r (c) of grain on time. These measured results correspond to the grain outside the ring which follows the epicycloid trajectory as shown by Fig. 2(a) and Fig. 6(b) III. The origin of polar coordinate is set to the center of the glass ring. The capitals A–C correspond to those in Fig. 6(b) III. The magnitudes of Fc and Fr at point B is smaller than that at point C.

The above force analysis is also applicable to the case (I). However, because the small cyclotron radius R1 is located outside the equilibrium line L in case (I), the periodical change of the cyclotron radius results in the hypocycloid trajectory as illustrated by Fig. 2(c). Particularly, if the grain is more closer to the glass wall, Fr1 becomes stronger, the petals would turn into cusps, which results in the formation of cuspate hypocycloid trajectory as illustrated by Fig. 2(d).

For the case (II), the grain meanders between the equilibrium line L and the glass wall. The centripetal forces near and far away from the glass wall are:

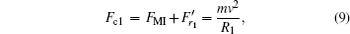
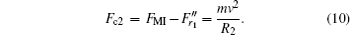
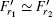
Obviously, the cyclotron radii R1 < R2. The cyclotron radius changes periodically as the grain travelling, which results in the hypocycloid motion. The above analysis is also applicable to the case (IV). In addition, if we assume due to the small radius r2 of the primary circle and add Eq. (9) and Eq. (10) together, then we have FMI ≃ (Fc1+Fc2)/2. From the measured Fc1 and Fc2 we can obtain that FMI is of the order of 10−11 N.

4. Conclusions and remarks

In this work, we have studied the cycloid motions of irregular grains (pine pollen) in a dusty plasma in a 2D horizontal plane. Hypocycloid motions are observed both inside and outside the glass ring. Epicycloid motion is observed only outside the glass ring. The radially confining potential from the sheath is experimentally measured, which play important role in the formation of cycloid motions of grains. Based on the force analysis and the measured trajectories of grain with high speed camera, the inverse Magnus force is obtained to be of the order of 10−11 N, and the value of the angular velocity is of the order of 105 rad/s. The observed cycloid motions of grains result from the periodical change of the cyclotron radius near and far from the glass wall. Additional comparison experiments with regular microspheres are performed in order to confirmed that the cycloid motions are distinctive features of a pine pollen immersed in a plasma.

Recently, some studies focused on the Magnus effect in optical manipulation,[29] in a Bose–Einstein condensate,[30] and in lattice models of superfluids.[31] They have revealed that the Magnus force is larger than that predicted by theoretical models and allows one to perform particle trapping. Our results have also revealed that the Magnus effect an irregular grain exhibited in plasma environment can not be negligible and would play important role on the complex motions of the grains. It is also suggested that these complex motions of irregular grains we observed could be found in fusion reactors because the grown or sputtered grain could have considerable angular speed of spin.

In addition, the vector of angular velocity of a spinning grain is not limited to the vertical direction as we discussed above. Due to the stochastic initial conditions of a dropped grain, this vector could point at other directions in three dimensional space. This means that the inverse Magnus force acting on a spinning grain could point out of the horizontal plane. Therefore, the inverse Magnus force together with the other forces will give rise to more complex motions of grains in three dimensional space. This will be the subject of a future study.

Reference
1Morfill G EIvlev A V 2009 Rev. Mod. Phys. 81 1353
2Fortov V EKhrapak A GKhrapak S AMolotkov V IPetrov O F 2004 Phys. Usp. 47 447
3Shukla P KEliasson B 2009 Rev. Mod. Phys. 81 25
4Chu J HLin I 1994 Phys. Rev. Lett. 72 4009
5Zhdanov S KNosenko VThomas H MMorfill G ECouëdel L 2014 Phys. Rev. E 89 023103
6Hou L JWang Y NMiskovic Z L 2005 Phys. Plasmas 12 042104
7Huang FYe M FWang L2004Chin. Sci. Bull.492150
8Wu JingZhang P YSun J ZZhang JDing Z FWang D Z 2008 Chin. Phys. B 17 1848
9Bonitz MHenning CBlock D 2010 Rep. Prog. Phys. 73 066501
10Ott TLöwen HBonitz M 2014 Phys. Rev. E 89 013105
11Feng YLiu BGoree J 2008 Phys. Rev. E 78 026415
12Liu D YWang D ZLiu J Y2000Acta Phys. Sin.491094(in Chinese)
13Carstensen JGreiner FHou L JMaurer HPiel A 2009 Phys. Plasmas 16 013702
14Saitou YIshihara O 2013 Phys. Rev. Lett. 111 185003
15Wang X GWang Z XWang C HGuo B 2002 Phys. Plasmas 9 4396
16Zou XLiu J YWang Z XGong YLiu YWang X G2004Acta Phys. Sin.533409(in Chinese)
17Baruah SDas N 2010 Phys. Plasmas 17 073702
18Tsytovich V NSato NMorfill G E 2003 New J. Phys. 5 43
19Karasev V YuDzlieva E SEikhvald A IErmolenko M AGolubev M SIvanov A Yu 2009 Phys. Rev. E 79 026406
20Hutchinson I H 2004 New J. Phys. 6 43
21Schwabe MKonopka UBandyopadhyay PMorfill G E 2011 Phys. Rev. Lett. 106 215004
22Liu F CHe Y FDong L F 2014 Phys. Plasmas 21 123503
23Basner RSigeneger FLoffhagen DSchubert GFehske HKersten H 2009 New J. Phys. 11 013041
24Melzer ATrottenberg TPiel A 1994 Phys. Lett. A 191 301
25Schwabe MZhdanov SRath CGraves D BThomas H MMorfill G E 2014 Phys. Rev. Lett. 112 115002
26Schubert GHaass MTrottenberg TFehske HKersten H 2012 Contrib. Plasma Phys. 52 827
27Borg K ISöderholm L HEssén H 2003 Phys. Fluids 15 736
28Weidman P DHerczynski A 2004 Phys. Fluids 16 L9
29Cipparrone GHernandez R JPagliusi PProvenzano C 2011 Phys. Rev. A 84 015802
30Turner A M 2009 Phys. Rev. Lett. 103 080603
31Sonin E B 2013 Phys. Rev. B 88 214513