† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 51404232), the China Postdoctoral Science Foundation (Grant No. 2014M561074), and the National Science and Technology Major Project, China (Grant No. 2011ZX05038003).
The threshold pressure gradient and formation stress-sensitive effect as the two prominent physical phenomena in the development of a low-permeable reservoir are both considered here for building a new coupled moving boundary model of radial flow in porous medium. Moreover, the wellbore storage and skin effect are both incorporated into the inner boundary conditions in the model. It is known that the new coupled moving boundary model has strong nonlinearity. A coordinate transformation based fully implicit finite difference method is adopted to obtain its numerical solutions. The involved coordinate transformation can equivalently transform the dynamic flow region for the moving boundary model into a fixed region as a unit circle, which is very convenient for the model computation by the finite difference method on fixed spatial grids. By comparing the numerical solution obtained from other different numerical method in the existing literature, its validity can be verified. Eventually, the effects of permeability modulus, threshold pressure gradient, wellbore storage coefficient, and skin factor on the transient wellbore pressure, the derivative, and the formation pressure distribution are analyzed respectively.
In modern times, these unconventional tight oil and gas reservoirs such as oil & gas shale reservoirs and low-permeable reservoirs have become new energy targets in petroleum engineering; and they play more and more important roles in the world’s energy consumption. Correspondingly, the studies of the kinematic principles of fluid flow in unconventional reservoirs and their applications in engineering problems have become a hot topic at present.
Abundant experimental and theoretical analyses[1–13] have demonstrated that the fluid flow in low-permeable reservoirs do not obey the conventional Darcy’s law; there exists a threshold pressure gradient (TPG). That is, the fluid flow happens only if the formation pressure gradient exceeds TPG. In particular, Cai[11] presented the analytical expressions for the flow rate and the velocity of non-Newtonian fluid flow in low-permeable porous medium, and also obtained the scaling relation between TPG and permeability through fractal approach.
Unlike the modeling of Darcy’s flow, the flow in porous medium with TPG is a nonlinear moving boundary problem. Figure
 | Fig. 1. Comparison between computed dimensionless formation pressure distribution curves with and without including TPG. |
In another way, if an angle α between formation pressure curve and distance is set to be on the moving boundary, TPG will be equal to the value of tangent α from the definition of TPG. When TPG tends to zero, the tangent of α will become zero gradually. Then the type of formation distribution curve will tend to a limit case i.e., Darcy’s flow.
Many relevant studies have proved that it is very significant to take into account the TPG in the modeling of fluid flow in porous medium in low-permeable reservoir, whether from reservoir engineering applications or theoretical modeling analysis. For example, the gas flow in water bearing tight gas reservoirs in consideration of TPG is investigated by Zhu et al.;[14] and through the analytical investigation, their presented mathematical model shows that due to the existence of TPG the reservoir energy is largely consumed near the wellbore. The research[15] by Zhu et al. shows that the considering of TPG in low-permeable reservoir simulation can improve the history matching precision in the relevant applications in Units X10 and X11 of Daqing Oilfield. In Yin and Pu’s study,[16] it is demonstrated through a pilot test in Chao 45 Block of Daqing Oilfield that the improved history matching degree can be reached under the condition of considering TPG in the simulation of surfactant flooding in low-permeable reservoir. Yao et al.[10] and Liu et al.[17] investigated a basic one-dimensional moving boundary problem of fluid flow in porous medium with TPG by an analytical solution method and a subsequent strictly verified numerical method. And it is concluded that it is very necessary to take into account the effect of TPG for the fluid flow in porous medium with TPG, for mathematical modeling in engineering applications.
In the actual oil and gas production, the fluid pressure in the development of oil and gas from low-permeable reservoirs decreases gradually with the production time. As a result, the rock skeleton, which bears the net overburden pressure of reservoirs, will be compressed and deformed. It can cause elastoplastic deformation of the rocks, and reduce the permeability of reservoir. Academically, it is defined as “stress-sensitive reservoir”.[18–23] However, as far as we know, in previous researches of the moving boundary problems of fluid flow in low-permeable reservoir, the effect of deformation of low-permeable rock has not been considered and evaluated yet.
Here, based on these aforementioned concerns, in consideration of the two prominent physical phenomena in the development of low-permeable reservoirs i.e., the existence of TPG and the stress-sensitive effect, a new coupled moving boundary model of radial flow in low-permeable reservoir is developed; a concept of permeability modulus[18,19,21,22] is introduced to reflect the effect of formation deformation on the permeability change. Besides, both the wellbore storage and skin effect are incorporated into the inner boundary conditions.
Abundant researches have been conducted on the analytical and numerical solutions for such moving boundary problems of fluid flow in porous medium with TPG. And current major solution methods include the integral approximate analytical method,[24] the Green function method,[25] the exact analytical solution by similarity transformation method,[17,26] coordinate transformation based numerical method,[10] and direct finite difference numerical method.[27] Owing to the strong nonlinearity and complexity of our presented coupled moving boundary model, a coordinate transformation based finite difference method[10] is adopted to numerically investigate the effect of physical parameters on the model solutions to the formation pressure and moving boundary. The utility of the numerical method can be attributed to its simple approach to converting the moving boundary problem into a problem with fixed boundary conditions, and then solving it by a stable fully implicit finite difference method on fixed spatial grids.
The problem considered involves the radial flow in an infinite low-permeable stress-sensitive reservoir with TPG. The reservoir is homogeneous, isotropic, and isothermal. And the single-phase horizontal flow does not have any gravity effect. Both the wellbore storage and skin effect[19] are considered. The Newtonian fluid and rocks are slightly compressible.
The schematic of the physical model is shown in Fig.
The fluid density is as follows:[24]

The porosity of the porous medium is as follows:[24]

The modified Darcy’s law for the fluid flow in the porous medium with TPG is as follows:[1]
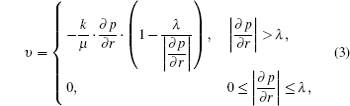
The permeability modulus γ (in unit atm− 1) is similar to the compressibility coefficient, and can be defined by the following equation:[18,19,21,22]
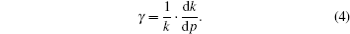
Coefficient γ plays an important role in the stress-sensitive effect on the rock permeability. It is a measurement of the dependence of the permeability on formation pressure drop. For practical engineering applications, it can be assumed to be constant.[18,19,21,22] Then the permeability of deformed rock in low-permeable reservoirs can be expressed from Eq. (

The continuous equation for the radial flow in the porous medium is as follows:[24]

Substituting Eqs. (

The initial conditions are as follows:


The inner boundary conditions in consideration of wellbore storage and skin effect with constant flow rate are

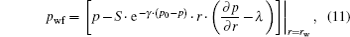
According to the definition of TPG, the moving boundary conditions are the same as the ones in Ref. [10] as follows:
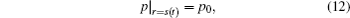
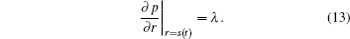
Equations (
The dimensionless variables are defined as follows:

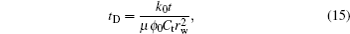

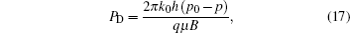

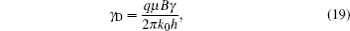
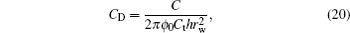

And then the dimensionless form of the coupled moving boundary model can be transformed equivalently. The governing equation is as follows:

The initial conditions are as follows:


The inner boundary conditions are as follows:
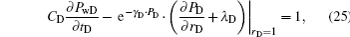

The moving boundary conditions are
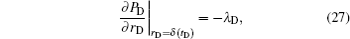
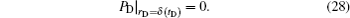
From Eq. (

Differentiating two sides of Eq. (

Substituting Eq. (
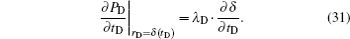
By using Eqs. (
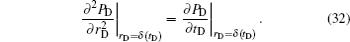
By Eqs. (
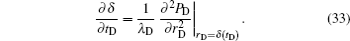
From Eq. (
In order to overcome the difficulty in discretizing space for the transient flow region with moving boundary, a spatial coordinate transformation method is used. It is the same as the one for the radial seepage flow problem with moving boundary in Ref. [10] as follows:

Through Eq. (


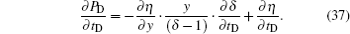
Expanding the term on the left-hand side of the governing equation i.e., Eq. (
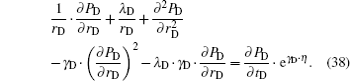
Substituting Eqs. (



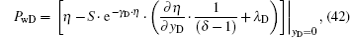




Substituting Eqs. (



Equations (
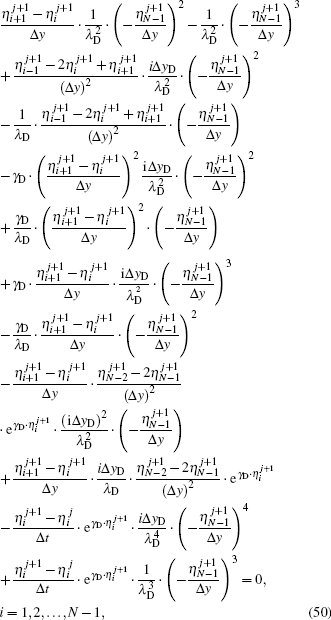

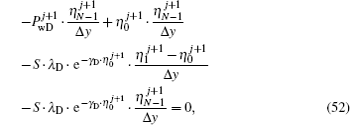
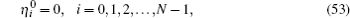

Equations (
The difference equation of Eq. (

Substituting Eq. (
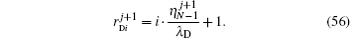
By Eq. (
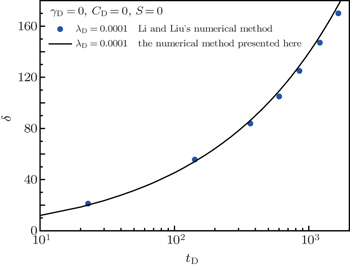
Li and Liu[27] have studied a moving boundary model of radial flow in porous medium with TPG without consideration of the stress-sensitive effect, nor wellbore storage nor skin effect. Its numerical solution is obtained by direct spatial discretization with fixed grids. In our presented coupled moving boundary model, if γD, CD, and S are all set to be zero, the coupled moving boundary model can be reduced to the same model as the one in Ref. [27]. From Eq. (
Figure
Figure
 | Fig. 5. Effects of dimensionless permeability modulus on transient wellbore pressure and its derivative for different values of γD. |
 | Fig. 6. Effects of dimensionless permeability modulus on formation pressure distribution for different values of γD. |
Figure
Figure
With respect to the dimensionless formation pressure, near the wellbore (see the enlarged semi-log plot in the inset of Fig.
Figures
From Figs.
Besides, from Fig.
Figures Effects of dimensionless wellbore storage coefficient on transient wellbore pressure and its derivative for different values of CD. Effects of dimensionless wellbore storage coefficient on formation pressure distribution for different values of CD.
From Fig.
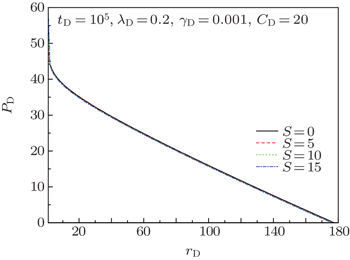
Figures
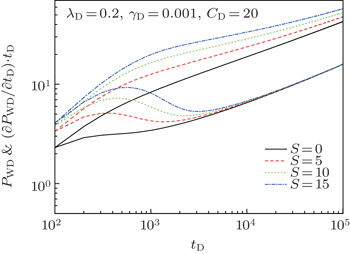 | Fig. 11. Effects of skin factor on transient wellbore pressure and its derivative for different values of skin factor S. |
A new coupled moving boundary model of radial flow in a stress-sensitive reservoir with TPG is built in consideration of the aforementioned two prominent physical phenomena in the development of low-permeable reservoir. A coordinate transformation based fully implicit finite difference method is adopted to obtain the numerical solutions of the nonlinear model. Its validity is also verified.
Some important conclusions from the numerical results analysis are obtained. The dimensionless permeability modulus, indicating the reservoir deformation, has little effect on transient wellbore pressure and its derivative. The more serious pressure drop caused by the formation deformation in low-permeable reservoirs mainly happens in the place near the wellbore. Unlike the scenario from the Darcy’s flow problem, the formation pressure distribution curves corresponding to nonzero TPG show a property of compact support; the log–log typical curves all turn upward, and the line representing the period of radial flow is not horizontal. The effect of dimensionless wellbore storage coefficient on the dimensionless formation pressure distribution is not very obvious, and it mainly affects the initial stage of transient wellbore pressure behavior. The skin factor has little effect on the dimensionless formation pressure distribution.