The research on abnormal light propagation, such as extraordinary optical transmission (EOT) or directional beaming through a subwavelength metallic aperture or slits, has attracted increasing interest in the last decade.^[1–8] Like the optical counterparts, the enthusiasm of studies about manipulating the acoustic wave is on the rise.^[9–23] Recently there were breakthroughs in acoustic metamaterials.^[24–27] Specifically, the active acoustic metamaterials were proposed, such as using active devices to break the reciprocity for nonreciprocal acoustics.^[28–30] Acoustic radiation pattern control has now gathered widespread attention in recent years due to its various application prospects in medical ultrasound instrumentation, secure communication, etc. In common cases, the acoustic wave will diverge in propagation, owing to the diffraction effect. Besides, the directivity of radiation pattern will fall off with the decrease of frequency. In order to save transmitted energy or retain the confidence of the signals, manipulating directional radiation is needed.

The pioneering work by Lu et al. on the transmission of an impinging acoustic wave through a one-dimensional acoustic grating with subwavelength apertures has proved an effective way to excite the phenomenon of extraordinary acoustic transmission (EAT).^[9] By investigating the beam from a subwavelength slit surrounded by periodic grooves, Christensen et al. successfully obtained a collimated wave,^[10] which was experimentally demonstrated by Mei et al.^[11] The underlying physics of EAT phenomenon is already intensively studied nowadays, which is mostly attributed to the contribution of acoustic surface evanescent wave (ASEW) and the interplay of the waveguide modes inside the apertures.^[12,13] Based on wave-vector analysis, a theoretical model of tunable directional acoustic beaming assisted by surface acoustic wave (SAW) has been proposed by using asymmetric surface gratings.^[14] Though these on-axis sound beams have good collimation effects, the fundamental mechanism inevitably brings many unwanted sidelobes into the radiation pattern. Recently, instead of adjusting the material properties throughout the propagation region,^[15–17] regulating surface impedance has been demonstrated as another valid way to manipulate radiation patterns.^[18–23] Owing to the presence of designed inhomogeneous impedance, steerable extraordinary reflection can be achieved.^[18,19] Meanwhile, the manipulation of EAT has been achieved through tuning structure topology or acoustic metasurface impedance.^[20–22] By optimizing surface impedances, our team has successfully obtained a dipole-like radiation pattern from a subwavelength slit, which conveys sound energy directly into the front region.^[23] Extending our previous studies of the surface impedance which is identical on both sides in the scheme, it naturally leads to the question of what we will obtain by breaking the surface impedance symmetry.

In this paper, we propose a scheme to tune the direction of an acoustic beam. As the boundary acoustic impedance can be changed by introducing Helmholtz resonators (HRs), we find that it is possible to obtain an inhomogeneous impedance boundary by rearranging the HRs. Using this method, asymmetric surface impedances can be obtained, which will result in a tunable directional radiation pattern.

The proposed structure consists of a subwavelength slit surrounded by two metal plates on both sides, whose surfaces are decorated with HRs. The schematic configuration is given by Fig. 1. For simplicity, we assume the HRs on both sides have the identical size and periods. D is the period of HRs; d_L (d_R) is the distance between the side-line of the slit and the HRs; d′ is the width of the central slit; h and l are the length and width of the neck of HRs, respectively; a and b are the width and length of the cavity of the HRs, respectively; H is the thickness of the sample. The structure is invariant in the z direction. The background medium is air, whose mass density and sound speed are denoted as ρ₀ and c₀ respectively. An acoustic plane wave impinges normally into the slit from the bottom. In order to simplify the analysis, the acoustic resistance and boundary layer effects in the narrow slit are ignored in the scheme.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Schematic diagram of subwavelength slit surrounded by two metal plates decorated with Helmholtz resonators (HRs).

Firstly, we survey the underlying mechanism of the effective impedance boundary caused by HRs. Without HRs, the specific acoustic impedance of a metal surface can be regarded as being infinite, Z_S → ∞, owing to a large difference between air and steel. Once the HR is introduced, on a subwavelength scale, the effective impedance of the region boundary can be expressed as

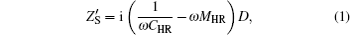
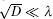
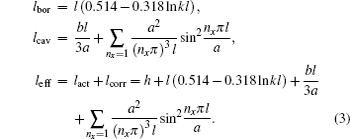
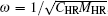
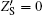
From these above equations, it is easy to deduce that arbitrary surface impedance can be obtained with optimized designed HRs size. In other words, we are capable of changing the original boundary into the desired condition with different HRs. Of course, the sizes of HRs should be within the practical working limits. In particular, when frequency meets the resonance condition, , then . This means that this surface region with HRs is converted from the original rigid boundary to a free boundary. Meanwhile, the other region without HRs will remain in a rigid condition. Thus if we change the distribution of HRs, then the boundary impedance can be adjusted, which can be used to generate the tunable acoustic radiation pattern.

Without loss of generality, we assume that d_L is the only control variable which contributes to the radiation pattern manipulating effect, and the configuration on the right side remains unchanged in the discussion. Full-wave simulations using finite-element method (FEM) are presented to verify our scheme. The parameters of the sample are set to be as follows: D = 8 mm, d_R = 1.5 mm, d′ = 2 mm, h = 0.5 mm, l = 1 mm, a = b = 5 mm, and H = 36 mm. The frequencies of incident acoustic plane waves are all set to be f = 8600 Hz, and the corresponding wavelength should be λ = c₀/f ≈ 39.9 mm. Since the period of HRs is much smaller than the wavelength, the premise of Eq. (1) is completely satisfied, i.e., , then we can regard the structure as being on a subwavelength scale, and view it as an acoustic metamaterial. Firstly, we let d_L = 1.5 mm, the impedances of both sides are totally identical, for the distributions of HRs on both sides are now the same. The transmitted beam looks very similar to the half-plane of a dipole radiation pattern, as shown in Fig. 2(a). Normally the radiation efficiency of dipole pattern is very low, but this dipole-like pattern in Fig. 2(a) has managed to overcome this shortcoming. The reason is that at this frequency point, a correction length caused by HRs is added to the original length of the slit; the sum of these lengths meets the requirement of Fabry–Perot resonance associated with waveguide modes in the centre slit, thus a transmission peak is achieved.^[23] In Fig. 2(b), d_L is assigned to 9.5 mm. A minor deflection occurs in the direction of the transmitted beam. As frequency equals 8600 Hz, we can deduce the effective surface impedance of the region with HRs from Eq. (1), which can be obtained to be . Meanwhile, the other region without HRs will remain in a rigid condition, whose specific acoustic impedance Z_S can be regarded as being infinite. Therefore the distribution of HRs turns the output surface of left sample into inhomogeneous boundary, consisting of both impedance boundary condition and rigid boundary condition. While the left sample becomes a ‘mixed’ one, the right sample decorated with a full set of HRs remains ‘pure’ impedance boundary. Owing to the asymmetric boundary conditions of both sides, the radiation pattern no longer maintains initial up-straight direction. The main energy of the beam is now delivered into the left region, with a deflection angle θ ≈ 15°. Comparing Fig. 2(a) with Fig. 2(b), it is natural to propose that the deflection angle θ be related to the distance between the side-line of the slit and the HRs d_L. To verify this postulation, we increase the distance further to d_L = 17.5 mm. From Fig. 2(c), a much more obvious deflection phenomenon can be observed, with a deflection angle θ ≈ 30°. The asymmetric level of two sides contributes to the variation of deflection angle. The whole relationship between d_L and the deflection angle θ is given in Fig. 2(d). With the increase of d_L, the left sample is gradually transited from impedance boundary into inhomogeneous boundary, and finally has a completely hard boundary. During the boundary transition, the main energy of transmitted acoustic beam from the narrow slit is more and more delivered into the left spatial region, i.e., the deflection angle of the radiation pattern is increasing. Besides, from the result, we can see that the most drastic changing section of the value of θ corresponds to the region when d_L < 30 mm. It leads to the conclusion that the location of HRs near the slit, i.e. the boundary conditions of those regions near the slit, is the key influential factor on the acoustic radiation pattern, which mostly dominates the beam deflection angle. It should be noted that all the radiation patterns shown in Fig. 2 have no evident indication of any sidelobe, which is significantly different from the existing acoustic directional beam tuning methods.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. ((a)–(c)) Simulated results of intensify patterns of a plane wave passing through the sample at f = 8600 Hz when dL = 1.5 mm, 9.5 mm, and 17.5 mm, respectively. (d) The beam deflection angle as a function of the distance between the left side-line of the slit and the HRs.

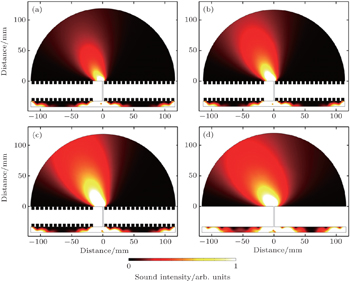
Comparing our study with the existing EAT or tunable beam manipulation schemes, one thing that should be mentioned is that our scheme is not just narrow-banded, i.e., the radiation pattern can occur in a relatively wide frequency range, which is demonstrated in Figs. 3(a)–3(c). While frequencies are assigned to three different values, the deflected beam angles in Figs. 3(a)–3(c) almost remain unchanged compared with the original radiation pattern in Fig. 2(c). Though the frequencies of the incident waves in Figs. 3(a)–3(c) no longer satisfy the FP resonance condition, the desired pattern still exists, but only with lower radiation efficiency.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (a)–(c) Simulated results of intensity patterns of a plane wave passing through the sample when f = 8300 Hz, 8400 Hz, 8500 Hz, respectively when giving dL = 9.5 mm. (d) Simulated result of intensity pattern of a plane wave passing through the undecorated sample when giving a specified impedance value at f = 8600 Hz.

The underlying mechanism is the effective impedance boundary caused by optimized HRs that contributes to these exotic radiation patterns, not the excitation of the SAW by inducing surface gratings. To confirm this, figure 3(d) shows two flat metal plates with no HRs nor surface gratings. The impedance of the output surface is directly given by in those regions with HRs as shown in Fig. 2(c), and the remaining area is assumed to satisfy the hard boundary condition. By comparing Fig. 2(c) with Fig. 3(d), one can easily find the coherence in these two results.

There are two reasons that need to be pointed out, which can explain the subtle differences between Figs. 2(c) and 3(d). First, owing to the absence of HRs, there is no correction length to compensate for the necessary thickness to meet the Fabry–Perot resonance requirement. Thus the radiation efficiency of Fig. 3(d) is weaker than that in Fig. 2(c). Second, the impedance values assigned to those boundaries are approximate, which do not satisfy the totally identical boundary condition as shown in Fig. 2(c).

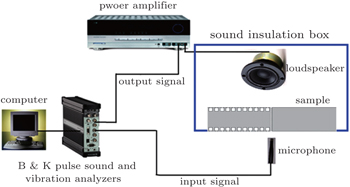
An experiment is conducted to further confirm the influence of asymmetric distribution of HRs on the radiation pattern directivity. The experiment is carried out in the anechoic chamber in order to eliminate the influence of the reflected waves. To avoid the diffraction from the edge of the sample, a sound insulation box is used. The pressure signal is picked up by a free-field 1/2-inch (1 inch, = 2.54 cm) microphone, which is fixed in a stepper motor controlled by the computer. The 3560B Brüel & Kjær Pulse Sound and Vibration Analyzer is used to generate output signals and collect input signals. The schematic diagram of experimental set-up can be found in Fig. 4.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Schematic diagram of experimental set-up of asymmetric effective impedance boundary.

The sample is made of steel, whose material parameters are as follows: mass density ρ = 7800 kg/m³, Young’s modulus E = 21.6 × 10¹⁰ N/m², Poisson’s ratio σ = 0.28, and sound speed c = 5200 m/s. The total width, height and thickness of each metal sample are 128 mm (containing 16 units, if decorated with HRs), 25 mm and 36 mm respectively. To avoid the complexity of sample processing, we choose d_L to be very large (d_L → ∞) and d_R = 1.5 mm. In other words, the left sample has no HRs, while the right one is full of HRs as shown in Fig. 5(a).

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (a) Top views of the sample fabricated by asymmetric distribution of periodical HRs and a single slit in the center (scale bar: 40 mm). (b) Experimental and (c) simulated results of intensity patterns of a plane wave passing through the sample.

Figures 5(b) and 5(c) show experimental and simulated data, respectively. The good consistence between the two pictures demonstrates that HRs are the main factor influencing the generation of the radiation pattern of the acoustic wave. The obtained result looks like a combination of the half left monopole pattern with the half right dipole pattern, which can be regarded as the consequence caused by rigid boundary and impedance boundary, respectively. The left part of the transmitted acoustic beam is far stronger than the right part, i.e., the vast majority of the transmitted sound energy is preserved in the left spatial region. Normally speaking, the transmitted radiation pattern from a slit should be omnidirectional with no directivity, like a half sphere. However, it is noted that our asymmetric radiation pattern has obvious directivity, which is almost parallel to the horizontal surface. This means that optimizing the locations of HRs is an effective way to manipulate radiation pattern, which can be used to deliver sound energy into the desired spatial region.

Owing to the presence of HRs, the effective impedance boundary or surface condition can be adjusted. By rearranging the HRs, asymmetric impedance boundaries surrounding a subwavelength slit are obtained, which plays a key role in producing the tunable acoustic radiation pattern. The feasibility of the proposal is verified by both simulation and experimental results. Compared with existing methods, our proposed scheme presents the radiation patterns with no sidelobes nor surface acoustic waves caused by structure, which conserves most of the acoustic energy in the main lobe. The low complexity facilitates the proposal realization and application. We believe that the enthusiasm of numerous research studies of effective impedance boundary is just starting and prospective applications of directional radiation in the fields such as secure communication or ultrasonic medical instrument would be expected.