† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11175094 and 91221205), the National Basic Research Program of China (Grant No. 2015CB921002), and partially supported by the Basic Research Fund of Beijing Institute of Technology (Grant No. 20141842005).
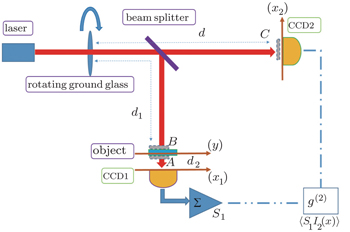
Lensless ghost imaging has attracted much interest in recent years due to its profound physics and potential applications. In this paper we report studies of the robust properties of the lensless ghost imaging system with a pseudo-thermal light source in a strongly scattering medium. The effects of the positions of the strong medium on the ghost imaging are investigated. In the lensless ghost imaging system, a pseudo-thermal light is split into two correlated beams by a beam splitter. One beam goes to a charge-coupled detector camera, labeled as CCD2. The other beam goes to an object and then is collected in another charge-coupled detector camera, labeled as CCD1, which serves as a bucket detector. When the strong medium, a pane of ground glass disk, is placed between the object and CCD1, the bucket detector, the quality of ghost imaging is barely affected and a good image could still be obtained. The quality of the ghost imaging can also be maintained, even when the ground glass is rotating, which is the strongest scattering medium so far. However, when the strongly scattering medium is present in the optical path from the light source to CCD2 or the object, the lensless ghost imaging system hardly retrieves the image of the object. A theoretical analysis in terms of the second-order correlation function is also provided.
Ghost imaging (GI), also known as correlated imaging, is a nonlocal imaging technology which retrieves an unknown object by measuring the second-order intensity correlation function between the test light field and the reference light field. The test light field goes to the object and then is collected by a bucket detector without spatial resolution, and the reference light field is detected by a spatial resolving detector without interacting with the object. The spatially point-to-point correlation of both entangled light source[1,2] and the thermal light[3–8] have been applied to achieve GI. GI also touches the fundamental principles of physics and aroused heated debates and discussions.[9–12] In addition, many different aspects of the GI have been studied, such as high-order GI,[13–15] compressed sensing GI,[16–20] differential ghost imaging (DGI),[21] normalized ghost imaging (NGI),[22] and so on.[23–30] In recent years, spatial light modulator (SLM) and digital micro-mirror device (DMD) are being developed, and they have also been employed in GI, for instance in the computational ghost imaging (CGI).[31,32] Based on the CGI, three-dimensional image and full-color image of the object have been obtained.[33,34] Furthermore, the influence of atmospheric turbulence, turbid media, or scattering media on GI have also been investigated.[35–42]
The lensless ghost imaging (LGI), where there is no lens in the optical paths, has drawn much attention in recent years.[43–50] In x-ray or γ-ray imaging, LGI possesses many advantages since the corresponding optical components, e.g., lenses, are very scarce, and are vulnerable to radiation damage. The longitudinal coherence length of LGI was studied in Refs. [51]–[55]. Zhang et al. studied the LGI of a phase object.[56] LGIs by measuring reflected photons were reported in Refs. [57] and [58]. For practical applications of LGI, the effects of atmospheric turbulence, turbid media, or scattering media in the optical paths must be studied.[59] In 2009, Cheng analytically derived a formula for LGI, taking into account of atmospheric turbulence, and showed that the turbulence can result in the degradation of the imaging quality.[60] In 2011, Shih et al. proposed a turbulence-free GI with non-factorizable, point-to-point correlation of thermal light.[61] Later, Bina et al. presented a scheme to achieve the backscattering DGI through the turbid media.[62]
It is desirable to study the influences of the strongly scattering medium on LGI. Ground glass is usually used as a scattering medium in optical systems.[63–65] Therefore, we use a pane of ground glass disk, which brings strong scatter and even attenuation, as the scattering medium in this work. We report the first (to the best of our knowledge) experimental investigation of the robustness of LGI in a scattering medium.
The paper is organized as follows. In Section 2, we present the experimental results and theory analysis of LGI system. Section 3 encompasses the study of the robust property of LGI when the scattering medium presents in different optical paths. The discussion and summary are given in Section 4.
The experimental setup is depicted in Fig.
In the classical interpretation of GI,[51] the normalized second-order correlation function between the two spatial points of test and reference beams plays a central role and reads
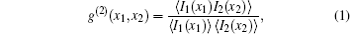

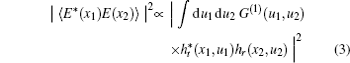
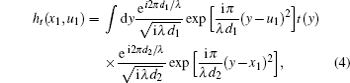
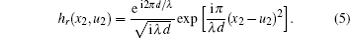
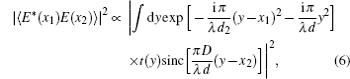
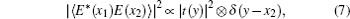
In this experiment, the traditional ghost imaging algorithm, i.e., normalized iteration algorithm is employed to retrieve the image of the object in the LGI,
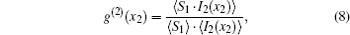
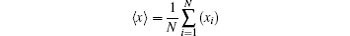
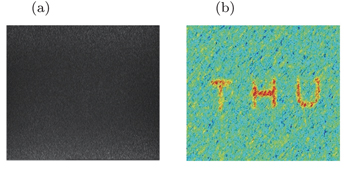
The classical image of THU is directly captured by CCD1 as depicted in Fig.
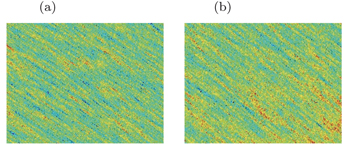
In the following, we report the investigation of the robust property for the LGI system when the strongly scattering medium (a 2-cm thick pane of ground glass disk) is put in the optical path. Firstly, the strongly scattering medium is placed in position A. Then, CCD1 is totally sheltered by the medium. The picture directly captured by CCD1 is showed in Fig.
 | Fig. 3. The strongly scattering medium present in position A: (a) image captured by CCD1 and (b) the ghost image of the THU with N = 2 × 104 iterations. |
The robust property against stationary strongly scattering medium in position A of the LGI system is easy to be understood. According to Eq. (

It is seen that β can be reduced, therefore, the LGI system with pseudo-thermal light is robust against the stationary strongly scattering medium in position A. Although CCD1 cannot collect all of the light scattered by the ground glass disk like the real bucket detector, part of the total light intensity is enough to retrieve the image of the object as shown in Fig.
 | Fig. 4. The ghost image of THU with the ground glass in position A which rotates in different angular frequencies of (a) 0.01 RPM (b) 0.1 RPM, and (c) 1 RPM respectively. |
Furthermore, when the strongly scattering medium is presented in other positions of this part of optical path from the object to CCD1, the only change is the value of β when the ground glass disk is stationary or the mean value of the β in the case that the ground glass disk is rotating. Hence, we can infer that not only position A but also the whole optical path from the object to CCD1 are robust against the strongly scattering medium for the LGI system with pseudo-thermal light.
When the strongly scattering medium is located in position B, no effective image could be retrieved from the LGI system as depicted in Fig.
In summary, we have studied the robustness of the LGI system with a pseudo-thermal light source using a pane of ground glass as the strongly scattering medium. When such a medium is located at position A, the LGI is robust against both the stationary and rotating strongly scattering medium. In the case that the strongly scattering medium is stationary, the total intensity of the test beam S1 only needs to be multiplied by an attenuation factor of β < 1 which could be reduced in the normalized second-order correlation function. When the strongly scattering medium is rotating, the attenuation factor β will vary with time, leading to β (t) = β + δ(t). However, as long as the roughness of the surface of the strongly scattering medium is distributed evenly, which means that the fluctuation of δ(t) is small, the fluctuation of the bucket signal will not be destroyed and the image quality of the LGI system could be maintained. When the strongly scattering medium is present in position B or C, the image of the object cannot be retrieved by the LGI system because the spatially point-to-point correlation function between the test and the reference beams has been destroyed by the strongly scattering medium.
In addition to the three positions reported here, we have also investigated other positions experimentally, finding that the results are similar to these three cases. These show that in the LGI system with a pseudo-thermal light source, the optical path from the object to CCD1 is of good robustness against the strongly scattering medium while the paths from the light source to the object and to CCD2 are not robust against the strongly scattering medium. This work can help us deepen the understanding of the LGI and will be of great benefit to the application of the ghost imaging.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 | |
| 63 | |
| 64 | |
| 65 |