Cite this Article
Zhou Xian-Ming, Cheng Rui, Lei Yu, Sun Yuan-Bo, Wang Yu-Yu, Wang Xing, Xu Ge, Mei Ce-Xiang, Zhang Xiao-An, Chen Xi-Meng, Xiao Guo-Qing, Zhao Yong-Tao. X-ray emission from 424-MeV/u C ions impacting on selected target. Chinese Physics B, 2016, 25(2): 023402  
Permissions
X-ray emission from 424-MeV/u C ions impacting on selected target
Zhou Xian-Ming1, 2, 3, Cheng Rui1, Lei Yu1, Sun Yuan-Bo1, 3, Wang Yu-Yu1, Wang Xing1, 5, Xu Ge1, 3, Mei Ce-Xiang4, Zhang Xiao-An4, Chen Xi-Meng2, Xiao Guo-Qing1, Zhao Yong-Tao1, 5, †,
Institute of Modern Physics, Chinese Academy of Sciences, Lanzhou 730000, China
School of Physical Science and Technology, Lanzhou University, Lanzhou 730000, China
University of Chinese Academy of Sciences, Beijing 100049, China
Normal College of Xianyang, Xianyang 712000, China
School of Science, Xi’an Jiaotong University, Xi’an 710049, China

 

† Corresponding author. E-mail: zhaoyongtao@mail.xjtu.edu.cn

Project supported by the National Basic Research Program of China (Grant No. 2010CB832902), the National Natural Science Foundation of China (Grant Nos. 11505248, 11375034, U1532263, 11275241, 11205225, 11105192, and 11275238), and the Scientific Research Program of Education Bureau of Shaanxi Province, China (Grant No. 15JK1793).

Abstract
Abstract

The K-shell x-rays of Ti, V, Fe, Co, Ni, Cu, and Zn induced by 424-MeV/u C6+ ion impact are measured. It is found that the K x-ray shifts to the high energy side and the intensity ratio of Kβ/Kα is larger than the atomic data, owing to the L-shell multiple-ionization. The x-ray production cross sections are deduced from the experimental counts and compared with the binary encounter approximation (BEA), plane wave approximation (PWBA) and energy-loss Coulomb-repulsion perturbed-stationary-state relativistic (ECPSSR) theoretical predictions. The BEA model with considering the multiple-ionization fluorescence yield is in better consistence with the experimental results. In addition, the cross section as a function of target atomic K-shell binding energy is presented.

PACS: 34.80.Dp;32.30.Rj;32.80.Aa;
Keyword:high energy heavy ions;ion–atom collisions;x-ray emission;
1. Introduction

Inertial Confinement Fusion (ICF) becomes more and more attractive for energy production in the field of thermonuclear research.[1–3] Two approaches are currently being investigated for heavy ion driven ICF: direct drive and indirect drive.[4] The former study shows that direct drive heavy ion target cannot be achieved through the thermal conduction alone, thus the indirect drive scheme is explored. One of the methods is that the fuel pellet is placed inside a hohlraum made of high-Z material, whose inner wall is heated by ion beams or lasers, and the resulting soft x-ray radiation from the walls drives the implosion with a much higher degree of symmetry.[5] The x-ray radiation drives the implosion, which requires not only sufficient conversion efficiency of the drive energy to the x-ray but also the highly spatial symmetry. Consequently, it is important to investigate the x-ray radiation in the interaction of high energy heavy ions beam with solid target.

The x-ray emission is an important consequential result from the inner-shell ionization during the interaction of highly charged ions with atoms, which provides significant information about atom configuration and the mechanism of such collisions.[6–9] In the middle and low energy region, lots of experimental work has been done on the inner-shell ionization by measuring the x-ray production cross sections, and many successful theories, such as binary encounter approximation (BEA)[10] and plane wave approximation (PWBA)[11] have been established to simulate the process. Especially, the energy-loss Coulomb-repulsion perturbed-stationary-state relativistic (ECPSSR) model,[12] which is a modification of PWBA by considering effects such as energy loss (E) and Coulomb deflection (C) of the projectile, modification of the atomic electron energy states through a perturbed stationary states model and adjustment of the electron mass due to relativistic effects (R), provides an excellent prediction of inner-shell ionization by light ions and has also been successfully applied to asymmetric heavy–ion collision of Z1 < Z2. However, in a very high energy region, it is not unclear that which theory is most suitable to predicting the x-ray emission induced by heavy ions, and the corresponding experimental investigations are rare.[13]

In the present work, the x-ray emission induced by high energy heavy ions is investigated. The K-shell x-ray production cross sections for 424 MeV/u h C6+ ions impacting on selected solid targets (Ti, V, Fe, CO, Ni, Cu, and Zn) are measured. The data are compared with various theoretical calculations of BEA, PWBA, and ECPSSR. The dependence of the cross section on the binding energy is investigated, and compared with that induced by relatively low energy protons.

2. Experimental methods

The experiment was performed at the cancer therapy terminal, which is specially designed for the heavy ion tumor therapy, at the national laboratory of Heavy Ion Research Facility in Lanzhou (HIRFL). The highly charged C6+ ions, produced and extracted from the electron cyclotron resonance (ECR) ion source, are accelerated by the main cooling storage ring (CSRm) with an energy of 430 MeV/u, and the beam quality is improved by the new generation electron cooler. The beam with a duration of 3 s, and a pulse distance of 15 s was directly extracted into air and impacted perpendicularly onto the target after collimation. The actual energy of the projectile impacting on target is about 424 MeV/u, and the corresponding uncertainty of the energies is no more than 0.22%. The beam size is about 5 × 5 mm measured by a CsI(Tl) crystal, and the beam intensity of impacting on the target is about 107 ions/pulse. The x-rays were observed by a silicon drift detector (SDD) which has an effective detection area of 7 mm2 and a 12.5-μm beryllium window in the front of the detector. The SDD was placed at 100 mm away from the target surface and at 135° with respect to the beam direction. The detector had an effective energy range of 0.5 keV–14.3 keV when the gain was selected at 100 and an energy resolution of about 136 eV at 5.9 keV when the peaking time was set to be 9.6 μs. It was calibrated using the standard radioactive resource 55Fe and 241Am before the experiment, and the efficiency was determined by transmission measurements. The targets for V, Co, Ni, Cu, and Zn each have a purity of 99.99%, while the purities of targets for Ti is 98% and 96% for Fe respectively. The thickness values are 4.02, 0.30, 0.10, 23.40, 0.05, 0.60, and 0.02 mm for Ti, V, Fe, Co, Ni, Cu, and Zn targets, respectively. The number of the incident projectiles are measured indirectly by a combination of a Faraday cup and the counts given by the counter fixed around the exit of the beam line terminal. In addition, for comparison, the data of lower energy proton are cited from our previous experiment.[14]

3. Results and discussion
3.1. Multiple-ionization induced by high energy C ions

Figure 1 shows the typical x-ray spectra induced by 424 MeV/u high energy C ions impacting on Ti, V, Fe, Co, Ni, Cu, and Zn targets. The L-shell x-rays are not recorded due to the strong absorption of the air and the low detection efficiency of the detector at low energy region. The two distinct identifiable K-shell lines are observed. The structures of the spectra are similar, except for the distinction of the x-ray energy. For all targets, the Kα includes Kα1 (2p3/2–1s) and Kα22p1/2–1s) x-rays However, the Kβ contains Kβ1(3p3/2–1s) and Kβ32p1/2–1s) x-rays for Ti and V, but Kβ1, Kβ3 and Kβ5 (3d–1s) for Fe, Co, Ni, Cu, and Z elements, respectively.[15]

Fig. 1. Typical x-ray spectra of Ti, V, Fe, Co, Ni, Cu, and Zn for 424 MeV/u C6+ impact.

In Fig. 2, the two x-ray peaks of V produced by high energy carbon ion impact are fitted by using a Gaussian program and compared with that induced by proton which has the same data as the singly ionized atom. It is obvious that a blue shift of about 40 eV is caused by the high energy ion impact. The similar results are obtained for other elements, as indicated in Table 1. As is well known, accompanied with the production of inner vacancy, the outer-shell can be multiply ionized during fast ion–atom collisions. This leads to the measured x-ray energy shifting to the high energy side, because the binging energies of the remaining electrons are perturbed as the screening of the nuclear charge is reduced with the multiple vacancies appearing. The L-shell multiple-ionization can be determined by analyzing the energy shift of the K x-ray in low-resolution measurement or KLn hyper-satellite x-ray intensity distribution in high-resolution crystal spectrometer. Here, according to the calculation results of multi-configuration Dirac–Fock,[16] the observed energy shift allows us to estimate about 2 ∼ 3 2p vacancies that are produced by the high energy heavy ion impact.

Fig. 2. Comparison of V K-shell x-ray induced by 424 MeV/u C ion impact with that by 200-keV proton impact.
Table 1.

K-shell x-ray peak positions and relative intensity ratios of Ti, V, Fe, Ni, Cu, and Zn for 424 MeV/u C ion impact. For comparison, the data by proton impact, which are in accordance with the data of the singly ionized atom, are also given.

.

Another effect of multiple-ionization is to change the fluorescence yield. The K-shell vacancy is mainly filled radiatively by x-ray emission or radiativelessly by Auger electron emissions or Coster–Kronig transitions. When the 2p electrons are multiply ionized, the K–L radiation transition rate is reduced because the 2p electrons are directly responsible for the Kα x-ray emission. Moreover, the rate of KLL Auger transition is diminished with the decease of 2p electrons. The total radiative and non-radiative rate are both constant. Thus, the K–M radiative transition rate is enlarged. Consequently, the Kβ fluorescence yield increases as Kα luorescence yield decreases. As listed in column seven in Table 1, the intensity ratio of Kβ to Kα x-ray is about 2 times larger than that produced by proton and photon for V, and about 1.5 times larger for Fe, Co, Ni, Cu, and Zn elements. This provides another possible evidence for the multiple-ionization of the target atoms by highly energy carbon ion impact.

3.2. X-ray production cross section induced by high energy C ions

Generally, the observed x-ray cross sections of the thin target can be extracted from the measured x-ray counts, according to formula of σx = Nx/[nNpεdft(Ω/4π)],[17] where n is the target atomic number in unit area. In the present work, the thickness values of the targets are 19.8, 17.0, 18.0, 17.9, 18.8, 21.7, and 28.4 μm for the Kα x-ray of Ti, V, Fe, Co, Ni, Cu, and Zn respectively, which are larger than the self-attenuation length. Thus the thin target cross section formula cannot be used immediately. The energy loss of the projectile in the target with a thickness of self-attenuation length is no more than 0.024 MeV/u, therefore, it is thought that the observed x-rays are induced by the projectiles with the same energy, even though they come from the different atomic layer. Taking the self-absorption of the target and the absorption of the air into account, the experimental x-ray production cross section for the thick target in the high energy region could be calculated from

where μ is the absorption coefficient, Nx is the obtained counts of the x-ray which are extracted by fitting the x-ray spectrum with Gauss function, ρ is the target atomic number in unit volume, Np is the number of the incident ions, εd is the detector efficiency, ft is the attenuation factor of the x-ray in the absorber set between the target and the detector, Ω is the solid angle, and L is the target thickness. Here, the total K-shell x-ray production cross section is obtained by summing up those cross sections that are separately measured from Kα and Kβ X-ray. The experimental errors are < 5% for the x-ray count statistic, < 10% for incident ions recording, < 6% for solid angle, respectively, and the maximal uncertainty of the total cross section is about 13% after error propagation.

Table 2 shows the experimental x-ray production cross sections calculated from Eq. (1), and the total results are shown in Fig. 3 as a function of the target atomic number and compared with various theoretical predictions that are derived from the ionization cross section with the single-ionized fluorescence yield, σx = σiω, where ω is the fluorescence yield. The cross sections are on the order of 103 barns and decrease with the increase of atomic number except for those of Ti and Fe which are smaller than the values that they should be due to the impurity of the target. The BEA calculations underestimate the data by a factor of about 1.5. The PWBA and ECPSSR model have small distinction in such a high collision energy region, and seem to present a better prediction to the experimental results. However, it is not the case, because the multiple ionization effect is not considered, which will change the simulations.

Table 2.

Target atomic K-shell x-ray production cross sections induced by 424 MeV/u C6+ ion impact on selected targets (Ti ∼ Zn). The unit 1 b = 10−28 m2.

.
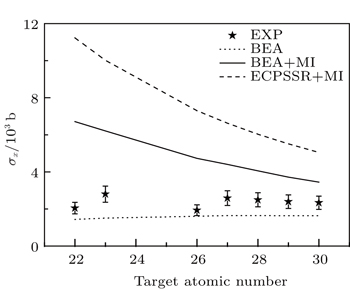
Fig. 3. Comparisons of the experimental K-shell x-ray production cross sections of Ti, V, Fe, Co, Ni, Cu, and Zn for 430 MeV/u C6+ ion impact with their theoretical calculations from BEA, PWBA, and ECPSSR models using the single ionization fluorescence yield.

As discussed in Subsection 3.1, multiple-ionization is involved in high energy heavy ion-atom collisions. Owing to the appearance of 2p-shell multiple vacancies, some of the non-radiative transitions are forbidden, and the K-shell fluorescence yield is increased. This can, in turn, lead to the enhancement of the x-ray production cross section. The theoretical calculations with considering the fully ionized fluorescence yield are shown in Fig. 4. After correction, the calculation of ECPSSR + MI gives a bigger overestimation to the experimental results. The BEA + MI model presents a better prediction than the ECPSSR + MI and gives a similar tendency to the present data. We think, during such high energy collisions, it is more reasonable to describe the target inner-shell ionization as binary-encounter-process rather than as plane wave approximation. Moreover, the fluorescence of multiple-ionization should be taken into account in determining the x-ray cross section.

Fig. 4. Experimental K-shell x-ray production cross sections of Ti, V, Fe, Co, Ni, Cu, and Zn for 430 MeV/u C6+ ion impact and theoretical calculations with considering the multiple ionization. The solid line represents the BEA prediction corrected by multiple-ionization fluorescence (BEA+MI). Dashed line refers to the ECPSSR simulation with using the multiple-ionization fluorescence (ECPSSR + MI).
3.3. X-ray production cross section as a function of the binding energy

The BEA model describes the ion-atom collision as the classical twobody process between the incident ions and the orbital electrons, and simulates the ionization cross section of the inner-shell for a definite energy transfer from the moving particles to the orbital electron of the target atoms and gives that in a close form as[10]

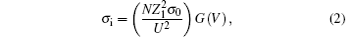
where N is the number of the objective electrons, Z1 is the projectile nuclear charger, σ0 = πe4, U is the binding energy of the orbital electron, and G(V) is a universal function of the scaled velocity V = vion/vi.

For V < 0.206, the G(V) is approximately expressed as 4V4/15, then the σi is written as[8]

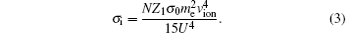
For the same incident ions with given energy, the ionization cross section is inversely proportional to the fourth power of binding energy, which has been demonstrated by many experiments, and the similar results have been observed in our previous experiment.[14]

When the scaled velocity is larger than 0.206, the function G(V) can be given algebraically as[18–20]

where

If this is substituted into Eq. (2), it seemed that the σi could not be simply represented by a monotonic function of binding energy. However, that is not what happened, and the ionization cross section should be a linear function of the binding energy in reality.

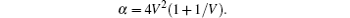
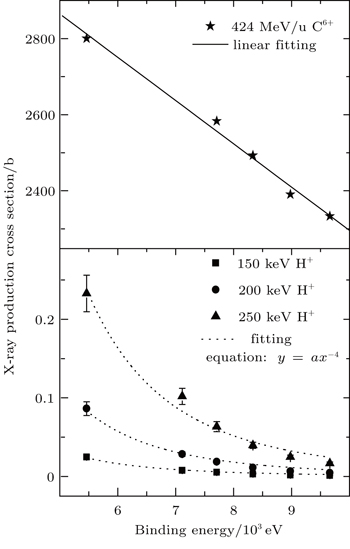
Generally, the K-shell x-ray production cross section is the result of inner-shell ionization cross section multiplies with the fluorescence yield. Therefore, it has a uniform functional relationship between the ionization cross section and the binding energy. Figure 5 presents binding energy dependent K-shell x-ray production cross sections of V, Co, Ni, Cu, and Zn induced by 424 MeV/u C ions and the comparative data produced by protons with energies of 150, 200, and 250 keV. It is obvious that the tendencies are different for the two opposite collision energy regions. In the lower energy region, the x-ray production cross section decreases with the increase of binding energy according to the function of σx = aU−4, which is in agreement with expression (3). However, for the high energy collisions, the experimental results decrease linearly with the increase of the target atomic binding energy.

Fig. 5. X-ray production cross sections each as a function of the target atomic binding energy induced by high energy C6+ ions and low energy protons.
4. Summary and conclusions

The K-shell x-ray emissions of the selected elements (Ti–Zn) are investigated for high energy (424 MeV/u) carbon ion impact. The x-ray production cross sections are calculated and compared with various theoretical estimations. It is indicated that in such high energy collisions, the L-shell electrons of the target atoms are multiply ionized, which leads to a blue shift of the K x-ray and an enlargement of the ratio of Kβ to Kα x-ray. The inner-shell ionization induced by high energy heavy ions can be simulated by the BEA model, but the effect of the multiple-ionization should be taken into account when determining the x-ray cross section, which decreases linearly with increasing the target atomic binding energy in the present work.

Reference
1Kidder R E 1976 Nucl. Fusion 16 405
2Tahir N APiriz A RWouchuk GShutov ALomonosov I VFortov V EDeutsh CHoffmann D H H 2009 Nucl. Instrum. Melthod A 606 177
3Tahir N ASpiller PShutov ALomonosov I VPiriz A RRedmer RHoffmann D H HFortov V EDeutsh CBock R M 2009 Translation of Plasma Science 37 1267
4Bodner S EColombant D GGardner J HLehmberg R HObenschain S PPhillips LSchmitt A JSethian J DMcCrory R LSeka WVerdon C PKnauer J PAfeyan B BPowell H T 1998 Phys. Plasmas 5 1901
5Roth MCowan T EKey M HHatchett S PBrown CFountain WJohnson JPennington D MSnavely R AWilks S CYasuike KRuhl HPegoraro FBulanov S VCampbell E MPerry M DPowell H 2001 Phys. Rev. Lett. 86 436
6Zhou X MZhao Y TRen J RCheng RLei YSun Y BXu GWang Y YLiu S DXiao G Q 2013 Chin. Phys. B 22 113402
7Mei C XZhang X AZhao Y TZhou X MRen J RWang XLei YSun Y BCheng RWang Y YLiang C HLi Y ZXiao G Q 2013 Chin. Phys. B 22 103403
8Wang XZhao Y TChen RZhou X MXu GSun Y BLei YWang Y YRen J RYu YLi Y FZhang X ALi Y ZLiang C HXiao G Q2012Acta Phys. Sin.61193201(in Chinese)
9Wang XZhao Y TChen RZhou X MXu GSun Y BLei YWang Y YRen J RYu YLi Y FZhang X ALi Y ZLiang C HXiao G Q 2012 Phys. Lett. A 376 1197
10McGuire J HRichards P 1973 Phys. Rev. A 8 1374
11Johnson D EBasbas GMcdaniel F D 1979 At. Data Nucl. Data Tables 24 1
12Lapicki GMcDaniel F D 1980 Phys. Rev. A 22 1896
13Zhang X AMei C XZhao Y TCheng RWang XZhou X MLei YSun Y BXu GRen J R 2013 Acta Phys. Sin. 62 173401 (in Chinese)
14Zhou X MZhao Y TCheng RWang Y YLei YWang XSun Y B 2013 Nucl. Instrum. Method B 299 61
15Kessler J E GDeslatts R DGirard DSchwitz WJacobs LRenner O 1982 Phys. Rev. A 26 2696
16Wang J JZhang JGu J GLuo X WHu B T 2009 Phys. Rev. A 80 062902
17Ouziane SAmokrane AZilabdi M 2000 Nucl. Instrum. Method B 161 141
18Gryzinski M 1965 Phys. Rev. 138 A305
19Gryzinski M 1965 Phys. Rev. 138 A322
20Gryzinski M 1965 Phys. Rev. 138 A336