High-order harmonic generation (HHG) from the non-perturbative nonlinear interaction between intense femtosecond laser pulses and atoms or molecules has been proven to be a reliable coherent source in extreme ultraviolet (XUV) and soft x-ray spectral regions.^[1,2] HHG driven by monochromatic or bichromatic laser in a collinear geometry has been extensively studied both experimentally^[3–6] and theoretically^[7–11] in the past years, the non-collinear HHG has received less attention, owing to its complex geometry. Nevertheless, the non-collinear geometry provides a natural way of separating the high harmonics from the fundamental beam, especially for the high harmonic radiation output coupling in an enhancement cavity of XUV frequency comb.^[12,13] It is also beneficial to better phase matching in HHG.^[14] The HHG process may be well described by the simple three-step model:^[15] an valence electron is firstly tunnel-ionized out of an atom in the strong laser field into the continuum state, then is accelerated and brought back to the atom by the laser field, finally recombines with the parent nuclei to emit a high energy photon. Quantum paths of the electrons are usually categorized by the excursion time in the continuum state, the shortest two of which are the well-known short and long trajectories. In a two-color scheme, HHG may be understood as high-order sum and difference frequency mixing.^[16] For instance, when the fundamental frequency ω₁ and the weak second harmonic ω₂ a beam are mixed, a harmonic photon ω is produced by absorbing (positive number) or emitting (negative number) q₁ photons with ω₁ and q₂ photons with ω₂. This gives another way of determining the quantum paths which are characterized by the photon number (q₁, q₂). A combination of q₁ photons and q₂ photons, which obeys the transition selection rules contributes to the HHG spectrum.^[5] All the contributions from different photon numbers (q₁, q₂) of the same frequency ω overlap spatially in the collinear two-color scheme, thus the individual quantum path is undistinguishable. The two-color HHG has been extended to non-collinear geometry by two^[17] and even multiple laser beams.^[18] Spatially discrete harmonics have been observed in non-collinear two-color HHG spectra which are explained in terms of the conservations of energy, momentum, and parity. Different paths (q₁, q₂) with the same harmonic frequency ω correspond to different propagation angles because of the momentum conservation, making it possible to separate individual quantum path in the space domain. The spatial separation of non-collinear HHG has been proposed to isolate single attosecond pulse^[19] and study the orbital angular momentum transferring from fundamental to HHG.^[20] Recently the phase matching effect and interference between adjacent paths in non-collinear HHG have been investigated^[21] as a frequency-domain analogy to the early work concerning the quantum path interferences for trajectories with different excursion times.^[22–24] The interference is explained by the dipole phase difference among harmonics from different source positions.

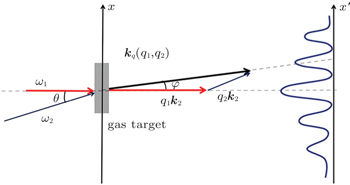
In the present paper, we numerically simulate the non-collinear HHG to provide a clear understanding of the quantum path interference. The frequency dependence of this interference is identified, which is attributed to the spatially dependent dispersion of the dipole phase of the atom. In our simulation the single atom response is calculated by solving time dependent Schrodinger equation (TDSE) in strong field approximation (SFA)^[25] with which a quantum analysis of the classical three step model is performed. In the SFA, the excited states and Coulomb field are not taken into account. The propagation effect in the gas target is ignored and only a single slice is considered as the HHG source in the calculation, which is infinitely thin in the propagation dimension and includes the beam profile in the lateral dimension. The far-field HHG spectra at a distance of 100 cm are calculated by the Huygens’ integral of the near-field distribution in Fresnel approximation.^[26] The driving field is composed of two Gaussian beams with frequencies ω₁ and ω₂ crossing with a small angle θ at the focus of both beams. A schematic of the simulation geometry is given in Fig. 1.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Schematic illustration of the simulation geometry. Two driving fields ω1 and ω2 enter the gas target with an angle θ. The polarization plane of the two parallelly polarized fields is determined by their wave vectors The propagation angle φ is determined by the direction of the momentum conservation. Dashed blue peak indicates the HHG in far-field x′ from different paths.

The simulation result for a strong fundamental field ω₁ (2 × 10¹⁴ W/cm², 800-nm wavelength) and a weak second harmonic ω₂ (0.2 × 10¹⁴ W/cm², 400-nm wavelength) with a crossing angle θ = 8.7 mrad is shown in Fig. 2(a). The pulse duration is 30 fs and the beam waist is 50 μm for both beams.

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. (a) Far-field spectrum of high-order harmonic radiation generated by driving fields ω1 (2 × 1014 W/cm2, 800 nm) and ω2 (0.2 × 1014 W/cm2, 400 nm) with 50-μm beam waist, 30-fs pulse length, and at an angle of 8.7 mrad in a slice of neon atoms placed at the focus. Far-field distributions are plotted as a function of delay for (b) 21st order, (c) 25th order, and (d) 29th order taken from panel (a).

Only a single slice of neon atoms placed at the focus was considered. The weak field ω₂ gives rise to even order harmonics as well as the off-axis discrete harmonics as shown in the spectra. The position of each discrete harmonic is determined by the conservation rules,^[17]

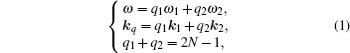
The propagation angle φ = θ q₂ω₂/ω predicted by the conservation rules is fitted well with our simulated spectra for orders lower than 25. The non-collinear HHG spectrum presents a spatial mapping of quantum paths determined by the photon absorption (emission) numbers (q₁, q₂). It is possible to distinguish different (q₁, q₂) paths for a certain harmonic frequency ω by their unique propagation angle φ.

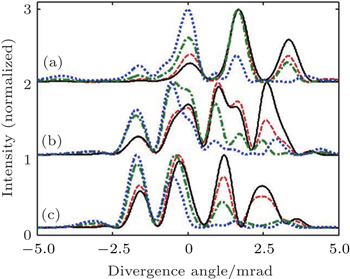
The angular gap of neighboring quantum paths Δφ = 2θ ω₂/ω is inversely proportional to the harmonic frequency ω. On the other hand the divergence of the discrete harmonic increases with frequency increasing.^[27] This makes the angular gap of discrete harmonics relatively large for low orders, and ensures the contribution of each quantum path to be resolvable in harmonic spectrum at far field. When the gap is comparable to or even smaller than the divergence of the discrete harmonics, the interference of adjacent paths appears. In Fig. 2(a) a significant deviation from the predicted propagation angle appears in high orders because the interference becomes more distinct for paths in higher orders due to their smaller spacings. The variations of far-field distribution as a function of the delay between two driving pulses for the 21st, 25th, and 29th order are shown in Figs. 2(b)–2(d). The position of main peaks in low harmonic orders do not change with delay, while an overall shift of the peaks with delay is observed in high orders(> 25).^[21] The adjacent quantum interference is modulated by the relative phase between the two driving pulses. There is a transition around 25th order revealing a mixed pattern of Figs. 2(b) and 2(d) where the shift is observed between the remaining main peaks as shown in Fig. 2(c). This pattern is formed due to the insufficient overlap in the intermediate harmonic orders. In the two-color HHG, the far-field divergence of a discrete emission from a particular path is expected to vary with the delay between the two-color fields.^[28] Therefore a different delay corresponds to a different overlap between adjacent paths. This effect is especially important for the intermediate orders because of their insufficient overlap. The adjacent paths from intermediate orders change between independence and overlap according to their divergence varying with delay. Thus the harmonic emission reveals an intermediate pattern between discrete and interference, as shown in Fig. 2(c).

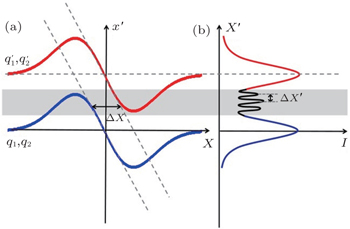
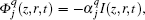
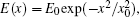
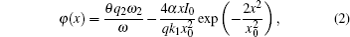
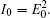
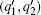
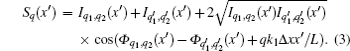
The interference between adjacent quantum paths may be understood in a framework of frequency chirp induced by the intensity-dependent dipole phase.^[29,30] The dipole phase is given by ^[31,32] where j refers to short (j = 1) or long (j = 2) trajectory contributing to the q-th harmonics, I(z,r,t) is the intensity envelope of the driving laser pulse ω₁, α_j depends on the electron excursion time in the continuum and its values for short and long trajectories are quite different. The discussion in this work is restricted to short trajectories which dominates the harmonic emission at the parameters used in Fig. 2(a), unless otherwise mentioned. The short trajectory is selected by the electron excursion time at a single atom response level. The intensity dependence of the dipole phase results in a curvature of the harmonic wave front, which is equivalent to a spatial frequency chirp Δf(x) = − ∂Φ (x)/∂x induced by the dipole phase. The divergence of the harmonic in the far-field is broadened by this curvature. Under the assumption of a Gaussian beam the far-field propagation angle of the q-th harmonic as a function of near-field radial axis x may be expressed as^[30]

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. Schematic illustration of the adjacent path interference. (a) The one-to-one imaging from near-field x to far-field x′ due to the spatial frequency chirp Δf(x) = − ∂Φ (x)/∂x, and (b) the corresponding far-field intensity distribution of the adjacent discrete harmonics ((q1,q2) and ). The shaded area indicates the interference region. The interference components from two paths are from opposite sides of the near-field separated by Δx. The far-field fringe interval is denoted by Δx′.

The interference fringe interval Δx′ is mainly determined by Δx. Since the HHG distribution usually concentrates in the central part of the laser beam where the chirp is almost linear, an approximation of Δx from the calculation of Eq. (2) may be written as

Fig. 4.

Figure Option ViewDownloadNew Window

Fig. 4. (a) Far-field spectra of high-order harmonic radiation generated by driving fields ω1 (2 × 1014 W/cm2, 800 nm) and ω2 (0.2 × 1014 W/cm2, 400 nm) with 100-μm beam waist, 30-fs pulse length, and at an angle of 17.5 mrad in a slice of argon at focus. (b) Dipole phase coefficient α (dots) retrieved from the spectra in panel (a) and calculated by the saddle point analysis (solid line), in units of 10−14 cm2/W.

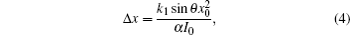
The effect of the dipole phase is not so straight forward. At certain intensity I₀, the coefficient α varies with harmonic order. A plot of α calculated by a saddle point analysis^[33] as a function of harmonic order for short trajectories in the mixed laser field ω₁ and ω₂ is shown in Fig. 4(b). The value of α increases monotonically with harmonic order because α is positively correlated to the excursion time that electrons spend in the continuum state. Larger harmonic order corresponds to a longer excursion time for short trajectories for a certain laser intensity. The increasing of α with harmonic order is partly responsible for the more obvious interference in high orders than that in low orders^[21] as shown in Figs. 2(b)–2(d) because larger α implies a larger divergence of individual discrete harmonic and the better overlapping of neighboring paths. The interference provides a way of retrieving α through Eqs. (3) and (4):

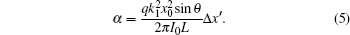
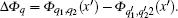
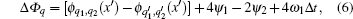
In order to improve the accuracy of the retrieval, larger beam waist 100 μm and crossing angle 17.5 mrad are chosen to acquire fine interference fringes as shown in Fig. 4(a). The values of coefficient α calculated for several orders from the fringes in Fig. 4(a) are denoted by dots in Fig. 4(b), which are on the same order of magnitudes as the theoretical value with an overestimate. The result shows that the simple physical picture given in Fig. 3 is suitable for describing the interference between adjacent quantum paths in the non-collinear HHG scheme qualitatively. An accurate theoretical model is required to provide more precise analysis of the interference process. The interference is also affected by driving laser intensity. For high orders at higher intensity, the spacing between different paths is smaller while the dipole phase is larger, which leads to a larger divergence of individual path. Thus the interference pattern for high orders at high intensity is more or less similar to the long trajectory at low intensity which has weaker main peaks and stronger interference. Besides the near-field separation Δx, the interference also depends on the phase difference The Φ_q1,q2 (x′) is determined by the phase between the two driving pulses. For adjacent quantum paths (q₁, q₂) and (q₁ – 4, q₂ + 2) when ω₂ = 2ω₁, it may be written as

The discussion above is also valid for long trajectory that has larger coefficient α and therefore more complicated interference pattern. Since short and long trajectories may be separated experimentally by phase matching^[34] or spatial filtering^[35] and theoretically by selecting the electron excursion time, it is reasonable to restrict the discussion to short trajectory for simplification.

To know the validity of our single slice gas target calculation, We calculate the spectra by a non-adiabatic two-dimensional propagation model modified in Ref. [36] as macroscopic effect plays an important role in HHG.^[37] In the case of non-collinear beams, radial asymmetry assumed in Ref. [36] is not available. Therefore the two-dimensional grid, which is in the plane formed by wave vector k₁ and k₂, is used instead of the three-dimensional grid (see supplementary information of Ref. [38]). The interaction region is 1 mm–3 mm long and centered at the beam focus. The gas pressure in the interaction region is 40 Torr (1 Torr=1.33322 × 10² Pa). Other parameters are the same as those in Fig. 2(a). The result in 1-mm gas target given in Fig. 5 is similar to the single slice result shown in Fig. 2(a) except for some small differences in the relative intensity among different quantum paths.

Fig. 5.

Figure Option ViewDownloadNew Window

Fig. 5. Far-field spectra for (a) 21st, (b) 25th, and (c) 29th order. The black solid line is extracted from the spectrogram in Fig. 2(a) without propagation effect included. The propagation effect is taken into account in 1-mm-thick (red dashed line), 2-mm-thick (green dot-dashed line), and 3-mm-thick (blue dotted line) gas target centered at the beam focus with the same parameters used in Fig. 2(a).

The discrete structure for low orders and the interference pattern for high orders survive after the 1-mm-long propagation in the gas medium. In 2-mm or longer gas target, the dominating peaks move towards the difference-frequency side (q₂ < 0). This shift may be explained by the additional geometrical phase mismatch term induced by the non-collinear geometry.^[21] The sign of additional mismatch term Δk_< = q₂θ (2q₂/q − 1)ω/ck_q is always opposite to q₂, i.e., Δk_< is negative for sum-frequency HHG (q₂ > 0) and it is positive for difference-frequency HHG (q₂ < 0). The negative neutral atom dispersion plays an important role in a long gas medium with moderate power,^[35] and such a dispersion may be compensated for by additional Δk_< in difference-frequency HHG. Therefore the difference-frequency HHG is more likely to add in a long medium, leading to the shift of the dominating peaks. The result verifies the validity of ignoring the macroscopic effect in order to achieve a brief and clear physical understanding, but only valid for short medium. Information from the single atom response is not destroyed by the macroscopic effect in a gas target as short as 1 mm.^[39]

In this work, the high-order harmonic radiation produced by two non-collinear beams with fundamental frequency at 800 nm and its weak second harmonic is numerically studied. We determine quantum paths by photon absorption (emission) number (q₁, q₂) and observe the spatial separation of the paths in the non-collinear scheme. Moreover, the interference between the adjacent paths is observed in high orders. The role of dipole phase in the interference is investigated and the coefficient α is retrieved from the interference fringe. The strong dependence on the CEP and delay between the driving pulses is also proven. The results in this work demonstrate the possibility of extracting the information about the quantum paths encoded in the interference spectra, which cannot be realized in a collinear scheme.