Graphyne,^[1–3] an sp- and sp²-hybridized carbon allotrope predicted by Baughman et al.,^[1] has become a new topic in two-dimensional (2D) materials since Li et al.^[3] and Liu et al.^[4] reported the successful preparation of the large area graphdiyne film by a cross-coupling reaction using hexaethynylbenzene. Besides, lots of theoretical research has been reported on the mechanical stability^[5–8] and electronic properties^[9–12] of graphyne as well as its derivates. Previous first-principle calculations^[9,13–15] have shown that α-, β-, and 6,6,12-graphyne possess the graphene-like Dirac cone band structures around the Fermi surface and they also exhibit small carrier effective mass values and high carrier mobilities like those of graphene. However, like graphene,^[16] it brings the same problem that pristine graphyne in the above cannot be used to build logical circuits with low power consumption at room temperature because it is a zero-gap semimetal. Bilayer stacking is a good choice to solve this problem since it can achieve the controllable semimetal to semiconductor transition under an external electric field.^[17–23] But the band modulation in bilayer graphyne has never been clearly clarified yet.

In this paper, based on first-principle calculations, we show how the electronic structure of bilayer α-graphyne is tuned by a perpendicular electric field and interlayer strain. Our results show that bilayer α-graphyne opens a gap under external electric field, which is consistent with the result in previous work.^[21] Though bilayer α-graphyne keeps the semimetal properties under interlayer strain, the field-induced gap can be modulated by interlayer strain over a wide range, which limitation exhibits a great increase with the decrease of interlayer distance. These results show that the combination of interlayer strain and electric field is an efficient method to tune the electronic structure of bilayer α-graphyne.

All calculations were performed using the VASP code^[24,25] with the Perdew–Burke–Ernzerhof (PBE) pseudo-potential^[26] and generalized gradient approximation (GGA) for the exchange–correlation potential. The projector augmented wave method (PAW)^[27] was applied with an energy cutoff of 500 eV for the plane wave basis. A gamma-centered 12 × 12 × 1 k-point sampling was used for the Brillouin-zone integration and a vacuum region larger than 15 Å was used to eliminate the interaction between the neighboring slabs. All the ionic coordinates were fully optimized until the forces were less than 0.01 eV/Å. Given the long-range vdW interaction, we employed the optB86b-vdW method^[28,29] to generate accurate equilibrium interatomic distance and energy. The external electric field was introduced by planar dipole layer method along the direction perpendicular to the graphyne planes.^[30]

We first discuss the structure and stability of bilayer α-graphyne. As shown in Fig. 1, there are four inequivalent C atoms denoted as A, b, a, and B in the unit cell of single layer α-graphyne. This atomic feature is similar to that of graphene, where the sublattices a and b corresponding to the two sp-hybridized C atoms in graphyne are absent. Thus, six nonequivalent stacking configurations of bilayer α-graphyne are denoted as AA, Ab, Aa, AB, ab, and aa, respectively (see ESI, Fig. S1 shown in Supplemental materials at the end of this paper).^[21] In order to determine the stablest stacking pattern, we perform total energy calculations on the six configurations of bilayer α-graphyne using optB86b-vdW methods within the DFT–GGA (generalized gradient approximation) as shown in Table S1 (ESI). It is found that the AB stacking with an optimized interfacial distance of 3.236 Å is more energetically favorable than other configurations, which is in good agreement with previous density functional theory (DFT) results.^[21] In this case, we will take the stablest configuration, AB stacking, as a model to study the electronic properties. The calculated electronic band structure of the AB stacking bilayer α-graphyne is plotted in Fig. 2. The interlayer atomic interactions make the linear bands two touching parabolic bands near the Fermi surface around the K point, which phenomenon is very close to that observed in bilayer graphene.^[18,19]

Fig. 1.

	Figure Option ViewDownloadNew Window
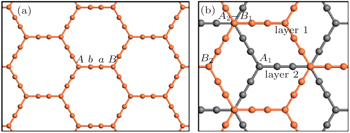	Fig. 1. (a) Geometric structure of single-layer α-graphyne and (b) bilayer α-graphyne with AB stacking. The inequivalent atoms are indicated and different layers are shown in different colors.

Fig. S1.

	Figure Option ViewDownloadNew Window
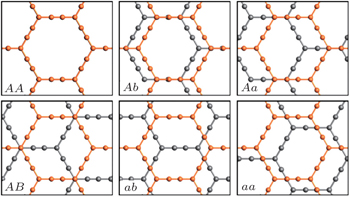	Fig. S1. Geometry structures of bilayer α-graphyne with six inequivalent stacking modes. Different layers are shown in different colors.

Table S1.

Table S1.

Table S1. Values of interlayer distance d and binding energy E of bilayer graphyne with six inequivalent stacking modes. . AA AB Aa Ab aa ab d/Å 3.6610 3.2359 3.3026 3.3790 3.3597 3.2904 E/eV 6.7898 6.7943 6.7929 6.7936 6.7926 6.7930

Table S1. Values of interlayer distance d and binding energy E of bilayer graphyne with six inequivalent stacking modes. .

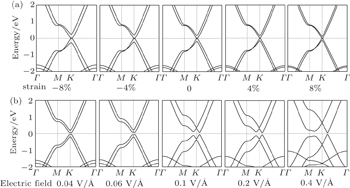
Strain is usually used to modulate the electronic properties in a 2D system.^[31–33] Specifically, strain has been widely predicted to modulate the band structure in bilayer graphene and bring graphene into practical application.^[17–20] Hence, it is of both fundamental and practical interest to examine the effect of interlayer strain on the electronic properties of bilayer α-graphyne. The interfacial strain is simulated by changing the interlayer distance between the two graphyne layers. The calculated band structures of bilayer graphyne with different interlayer distances are shown in Fig. 2(a). Like bilayer graphene,^[19] the band structure of bilayer graphyne shows a transforming trend from a parabolic spectrum near the Fermi energy to a linear spectrum by increasing the interlayer distance. This is because the interlayer atomic interactions decrease with the rising of interlayer distance. This phenomenon can also be seen in the conduction-band minimum (CBM) +1 and valence-band maximum (VBM) −1. When bilayer graphyne is compressed, the CBM+1 and the VBM–1 are pushed f3.e farther away from the Fermi surface, indicating strong interlayer coupling; on the contrary, when bilayer graphyne is under tensile strain, the CBM+1 and the VBM–1 come closer to the Fermi surface with the trend of dividing it into two single-layer graphynes, implying the weaker interlayer coupling.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (a) A series of band structures of bilayer graphyne under strains of ±8%, ±4%, and 0, without external electric fields. (b) Band structures of strain-free bilayer graphyne under electric fields of 0.04, 0.06, 0.1, 0.2, and 0.4 V/Å.

Next, we explore the electronic properties of bilayer graphyne under a vertical electric field E_ext. The band structures of bilayer graphyne under various fields are shown in Fig. 2(b). It is notable that when there is no external electric field, the CBM and VBM are degenerated at the K point, rendering bilayer graphyne a zero gap semimetal. When applying an electric field, the CBM and VBM split away from the Fermi surface, causing a Mexican-hat-like band structure^[18] around the E_F. As the field increases, the gap increases sharply and reaches a maximum value of about 120 meV at 0.1 V/Å. Then the gap decreases slowly as the electric field further increases. We attribute this to the strong screening^[18,34] between the up-down layers under high electric field as shown in the interlayer charge redistribution in Fig. 4. These results indicate that a vertical electric field does open an energy gap in bilayer graphyne.

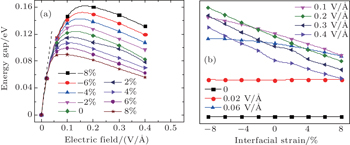
As mentioned above, interlayer strain cannot open the gap of bilayer graphyne, but it plays an important role in the interlayer coupling in bilayer graphyne. Given that both strain and electric field are feasible tools in tuning the electronic properties of materials in actual device designing, it should be interesting to investigate their combined effect. Here in this work, we demonstrate the important role of strain played in the electronic properties of bilayer graphyne under electric field. The energy gap variations with electric field and interlayer strain are shown in Fig. 3. It is found that the range of the gap modulation varies a lot with electric field, and all the strained bilayer graphyne exhibits the same trends with the rising of electric field. For instance, under 4% compressive strain, when the electric field is weaker than 0.02 V/Å, the band gap increases sharply with a rate of 0.272 eV per V/Å, which is a little smaller than the rate of bilayer graphene (0.294 eV per V/Å).^[19] Then the gap reaches a maximum value of around 131 meV and will decrease slowly as the electric field further increases. Besides, it is notable that the interlayer strain indeed helps to modulate the field-induced gap. From Fig. 3(a), we can see that under the same electric field, bilayer graphyne shows a larger field-induced gap under compressive strain than under tensile strain. We attribute the gap modulation to the collaboration between the strain and electric field. There is a critical electric field value to switch on the strain effect. Once the critical electric field is reached, the strain effect will help to modulate the gap. We can see clearly in Fig. 3(b) that the critical value here is around 0.02 V/Å. When the electric field is lower than that value, only the electric field works on the bilayer, so the variation of energy gap is insensitive to the interlayer distance; when the external electric field is larger than 0.02 V/Å, the energy gap decreases linearly with the increasing of interlayer distance, showing a wide range of gap modulation via interfacial strain. In addition, the reducing rate of the gap under a high electric field is larger than the rate under a low field. These results show a great prospect for tuning the energy gap of bilayer α-graphyne by the combined effect of interfacial strain and electric field and, at the same time, also motivate us to investigate the mechanism behind the phenomenon.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (a) Variations of the energy gap with electric field under different strains. The dashed line on the left of the curves indicates the linearly increasing gap with a slope of 0.272 eV per V/Å. (b) Variations of the energy gap with the interlayer strain at different electric fields.

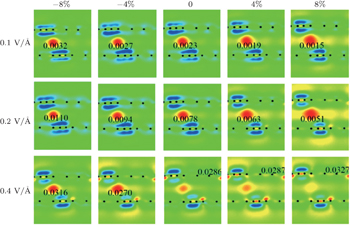
To further study the mechanism of the strained bilayer graphyne under external electric field, we plot the charge density difference ( where and ρ_bilayer are the charge densities of the bilayer graphyne with and without external electric field, respectively) of the system in Fig. 4. It is clearly seen that with the relatively low vertical electric field, charge is mainly accumulated in the interlayer region of the A2 and B1 atoms in strain-free bilayer graphyne. It is slightly suppressed under the tensile strain; while in the compressed bilayer graphyne, the interlayer charge accumulation is more concentrated. It should be noted that the overall charge distribution remains essentially unchanged. These findings can clarify the phenomenon (Fig. 3(b)) of small energy gap variation via changing interlayer distance under weak electric field. In contrast, the charge accumulation changes significantly when strong electric field is applied. As shown in Fig. 4(b), the interlayer charge accumulation is more remarkable in the compressed bilayer graphyne than in the stretched one, resulting in the increase of energy gap from 83 meV to 131 meV. Meanwhile, the relative charge disparity between the intralayer and interlayer regions become larger as the external electric field grows, especially in the tensile-strain bilayer graphyne, causing the slow decrease in energy gap.

Fig. 4.

	Figure Option ViewDownloadNew Window
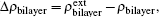
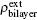
	Fig. 4. Projections of the charge density difference to the {100} surface under strains of ± 8%, ± 4%, and zero in the fields of 0.1, 0.2, and 0.4 V/Å. The value and location of the largest charge density difference (in units of e/Å3) are shown in each panel.

In this work, we systematically investigate the electronic properties of bilayer α-graphyne under interlayer strain and electric field by first-principle calculations. The combined effect of strain and electric field can efficiently modulate the energy gap of the bilayer structure over a wide range of interlayer distance and electric field, which stems from the novel interlayer charge redistribution. The tunable energy gap in bilayer α-graphyne provides robust and viable applications in the future mechanical-electric devices.