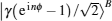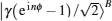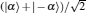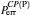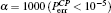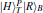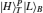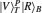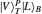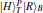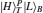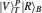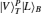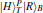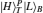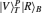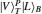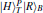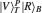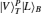† Corresponding author. E-mail:
We propose an arbitrary controlled-unitary (CU) gate and a bidirectional transfer scheme of quantum information (BTQI) for unknown photons. The proposed CU gate utilizes quantum non-demolition photon-number-resolving measurement based on the weak cross-Kerr nonlinearities (XKNLs) and two quantum bus beams; the proposed CU gate consists of consecutive operations of a controlled-path gate and a gathering-path gate. It is almost deterministic and is feasible with current technology when a strong amplitude of the coherent state and weak XKNLs are employed. Compared with the existing optical multi-qubit or controlled gates, which utilize XKNLs and homodyne detectors, the proposed CU gate can increase experimental realization feasibility and enhance robustness against decoherence. According to the CU gate, we present a BTQI scheme in which the two unknown states of photons between two parties (Alice and Bob) are mutually swapped by transferring only a single photon. Consequently, by using the proposed CU gate, it is possible to experimentally implement the BTQI scheme with a certain probability of success.
Quantum communication involves the transfer of information (quantum or classical) from one place to another by using quantum phenomena such as quantum key distribution,[1–6] quantum teleportation,[7,8] quantum secure direct communication,[9–12] and quantum secret sharing.[13] Quantum operations play a very important role in the experimental realization of optical quantum information processing (QIP) with a certain success probability. Reliable quantum operations can be performed by realizing the photonic multi-qubit gates, such as the arbitrary controlled-unitary (CU) gates.
Cross-Kerr nonlinearities (XKNLs) have been extensively studied both theoretically and experimentally for implementing feasible photonic multi-qubit gates. In principle, because the XKNL effect can induce efficient photon interactions, the photonic multi-qubit gates can be implemented by using far fewer physical resources than linear optical schemes.[14–16] Nemoto and Munro proposed nearly deterministic controlled gates by using ancilla photons, linear optical elements, and quantum non-demolition (QND) detectors based on weak XKNLs, X-homodyne measurements, and feed-forward schemes.[17] In 2009, Lin and Li presented an almost deterministic controlled-path (C-path) gate[18] by using weak XKNLs and X-homodyne measurements. Thereafter, similar schemes for implementing photonic multi-qubit gates[19–23] were developed for QIPs via weak XKNLs and X-homodyne measurements. Further, photonic multi-qubit gates,[24–27] which can reduce the nonlinear phase shift or the strength of coherent state via weak XKNLs, coherent superposition states (CSSs), and P-homodyne measurements for the same error probability, were investigated. These gates[24–27] not only increase the experimental realization feasibility but also enhance the robustness against decoherence.
However, decoherence (by loss of photons) is unavoidable when a coherent state (probe beam) is transmitted through a fiber in practice. Owing to decoherence, the state of photons (signal) evolves into a mixed state after the homodyne measurements.[28–31] Consequently, the fidelity of the optical multi-qubit gate will decrease. Fortunately, Jeong[30] has shown that decoherence can be made arbitrarily small simply by increasing the amplitude of the coherent state and by applying the displacement operator D(−α) to the coherent state and photon-number-resolving (PNR) measurements. In 2010, Wittmann et al.[32] showed that the performance of a displacement-controlled PNR measurement is better than that of a homodyne receiver for discriminating the coherent states. Furthermore, the optical multi-qubit or controlled gates,[33–38] exploiting the QND (PNR) measurement via weak XKNLs and two quantum bus (qubus) beams, were proposed so that XKNL (coupling phase shift) of −θ and the displacement operator D(−α) on the probe beam can be removed.
As mentioned in the above descriptions, the development of multi-qubit gates, in which the XKNLs and various measurement strategies were utilized for deterministic and feasible realization,[17–38] provides reliable performance and an experimental implementation of optical QIP schemes, such as the quantum communication scheme,[19,23,27] the generation of an entangled state,[22,24–26,39–41] the deterministic Bell-state measurement,[19,21,42,43] the entanglement purification,[44–46] and the entanglement concentration.[47–49] Thereafter, the optical QIP schemes, based on the implementation of multi-qubit gates via weak XKNLs, have been also investigated.
In this paper, first, we propose a deterministic and experimentally feasible CU gate, which is composed of consecutive operations of a C-path gate[34,35] and a gathering-path (G-path) gate via weak XKNLs, the qubus beams, the QND (PNR) measurements, and feed-forward schemes. Compared with the existing multi-qubit gates[17–27] using XKNLs, coherent states or CSSs and homodyne measurements, for the same error probability, the nonlinear phase shift θ or the amplitude of coherent state α required in our CU gate will be shown to be relatively small. In addition, motivated by Refs. [33]–[38], we, in our CU gate, utilize the qubus beams and the QND (PNR) measurements without the displacement operator for reducing decoherence (by loss of photons). Thus, when this CU gate is experimentally implemented, the feasibility is improved and decoherence is reduced. Subsequently, by using the proposed CU gates, we present a bidirectional transfer of quantum information (BTQI) for two unknown states of photons that are mutually exchanged between Alice and Bob, by transmitting only one photon.
The rest of this paper is organized as follows. In Section 2, we present a CU gate obtained by consecutive operation of a C-path gate[35,36] and a G-path gate via weak XKNLs, the qubus beams, the QND (PNR) measurements, and feed-forward schemes. Furthermore, we show that when compared with the existing multi-qubit gates[17–27] using the coherent states or CSSs and homodyne measurements, our CU gate exhibits improved feasibility of the experimental implementation and enhanced robustness against decoherence by using the qubus beams and the QND (PNR) measurements. In Section 3, we propose a BTQI scheme in which two unknown photons between Alice and Bob are mutually transferred by transferring only a single photon via optical elements such as beam splitters (BSs), spin flippers (SFs), polarizing beam splitters (PBSs), 45-PBSs, photon detectors (PDs), and CU gates as described in Section 2. Finally, in Section 4 we discuss the success probability and experimental implementation of the proposed CU gate and BTQI scheme.
Now we consider two types of photon polarizations: circular polarization (|R〉 is right- and |L〉 is left-circular), and linear polarization (|H〉 is horizontal and |V〉 is vertical). The relationships between the two types are given by
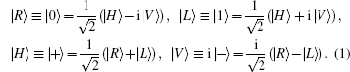
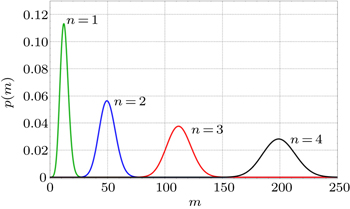
Thus, the circularly polarized states correspond to the eigenstates of σZ: {|R〉 ≡ |0〉,|L〉 ≡ |1〉}, and the linearly polarized states correspond to the eigenstates of σX: {|H〉 ≡ |+〉,|V〉 ≡ i |−〉}. We introduce the XKNL for explaining the CU gate. The XKNL’s Hamiltonian is HKerr = ħ χ N1 N2, where Ni is the photon number operator and χ is the strength of nonlinearity in the Kerr medium. We assume that |n〉i represents a signal state of n photons, and |α〉j is a coherent state (the probe beam). After passing through the Kerr medium, the signal-probe system state is changed into UKerr |n〉1 |α〉2 = ei θ N1 N2 |n〉1 |α〉2 = |n〉1 |α ei nθ〉 2, where θ = χt and t is the interaction time.
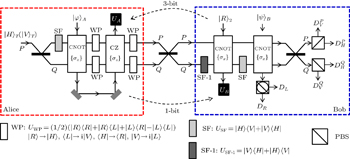
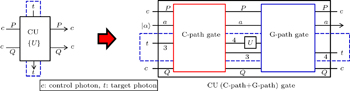
Now, we propose a deterministic CU gate that is composed of consecutively performing C-path gate,[34,35] an arbitrary unitary operator U, and a G-path gate using the XKNLs, the qubus beams, the QND (PNR) measurements, the feed-forwards, and linear optical elements such as 45-PBSs and BSs, which is shown in Fig.
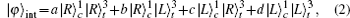
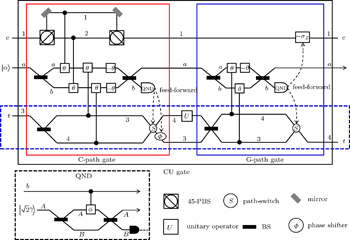 | Fig. 1. Schematic diagram of CU gate (black box), which is comprised of the consecutive operation of a C-path gate (red box on the left)[34,35] and a G-path gate (blue box on the right) using XKNLs, the qubus beams, the QND (PNR) measurements (dotted line black box), and feed-forwards. The CU gate is composed of three parts: the C-path gate, the operator U, and the G-path gate. First, in the C-path gate, the two photons c and t (dotted line blue box) in the input state (signal) induce controlled phase shifts θ in the two qubus beams (probe) by the XKNLs interaction. Then, the linear phase shifters −θ are operated on the two qubus beams. Subsequently, we measure the probe beam on the path b via the QND (PNR) measurement,[33–38] which can precisely discriminate the number of photons |n〉b in the probe beam on the path b. According to the measurement outcome |n〉b of the QND (PNR) measurement, we determine whether to operate the phase shifter Φ and the path-switch S on the target photon t by feed-forward. After passing the C-path gate, the target photon path is split according to the control photon polarization. The target photon goes through path 3 (or 4) when the control photon is |R〉 (or |L〉). In the second step, the unitary operator U on path 4 is applied to the target photon. In the third step of the G-path gate, the XKNLs induce phase shifts θ according to the target photon t, and then the linear phase shifter −θ is performed on the qubus beam on path a. For gathering the target photon on the split path, we finally apply the unitary operator −σZ to the control photon, and the path-switch S to the target photon via the feed-forward, depending on the measurement outcome |n〉b of the QND (PNR) measurement. Consequently, the CU gate performs a controlled-unitary (CU) operation on the input state. |
In the C-path gate[34,35] as shown in Fig.
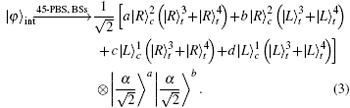
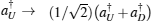
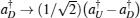
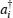
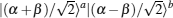
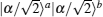
Subsequently, the linear phase shifters −θ are applied to the qubus beams, and then the signal-probe system is transmitted into 45-PBS (photon c) and BS (two qubus beams). The transformed state |φ〉01 of the signal-probe system will be
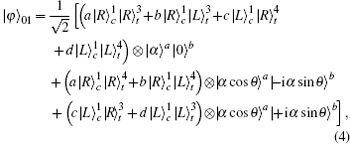

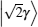
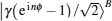
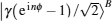
If the QND (PNR) measurement result is |0〉B, the output state |φ〉CP of the C-path gate is the first term in Eq. (
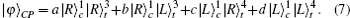
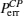
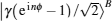
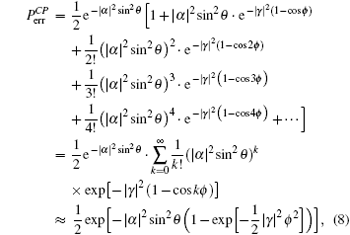
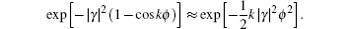
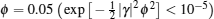
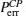
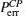
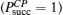
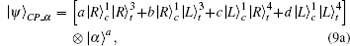
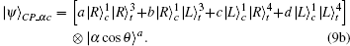
In the second step, the target photon in the state |ψ〉CP, in Eq. (

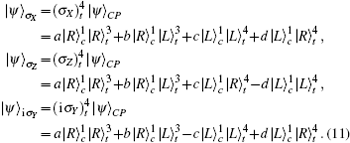
In the G-path gate of the third step as described in Fig. 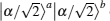
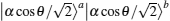
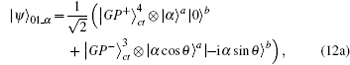
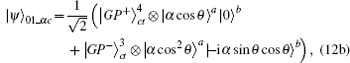
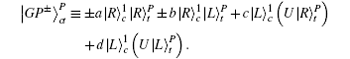
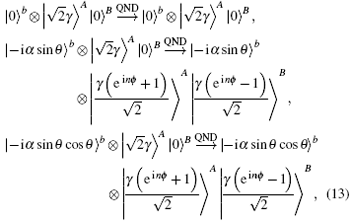
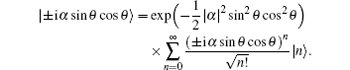
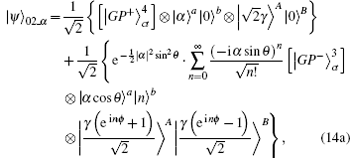

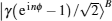
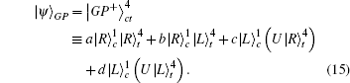
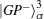

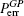
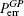
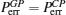
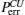
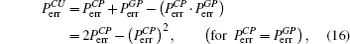

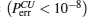
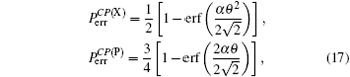
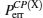
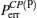
Table 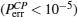
The BTQI scheme as described in Fig.
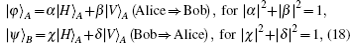
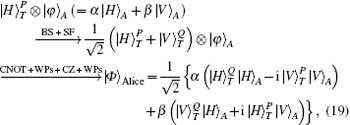
In Fig.
On Bob’s side, after the photon T of the state |Φ〉Alice passes through the BS, Bob performs the SF-1 (USF − 1) as described in Fig.
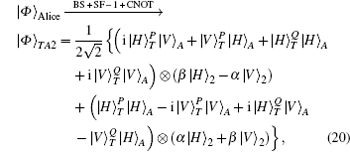
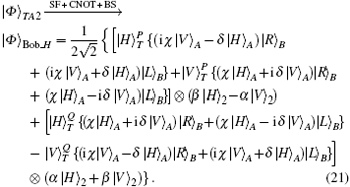
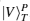
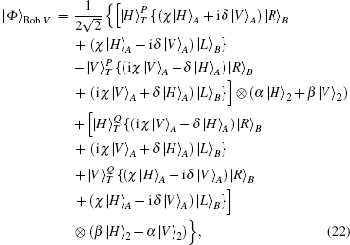
To measure the paths and polarizations of the photons, Bob transmits the photon T to the PBSs and the photon B to the 45-PBS. Because |H〉 (|R〉) is transmitted and |V〉 (|L〉) is reflected by the PBS (45-PBS), Bob can measure both the path and the polarization of photon T in the {|H〉T,|V〉T} basis by using PDs 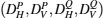
| Table 2. Collapsed states of the photons (photons A and 2) and the suitable unitary operations (UA,UB), depending on Alice’s initial polarization and Bob’s measurement outcomes. . |
In this paper, we propose a BTQI scheme, which achieves mutual transmission of two unknown states |φ〉A,|ψ〉B of photons between Alice and Bob, which do not directly send unknown states of photons (A,B) but instead use a classical channel to send the information about the states of photons and then utilize the information to reconstruct the unknown states. In our protocol, both Alice’s unknown state |φ〉A and Bob’s unknown state |ψ〉B are simultaneously transmitted to the other’s site. Thus, the two participants in our protocol simultaneously become both message senders and message receivers by directly transferring only a single photon T.
Because the BTQI scheme is based on the CU gate, the success probability and feasibility of realization of the proposed scheme (BTQI) strongly depend on the nearly deterministic performance and the experimental implementation of the CU gate, which can be operated by the consecutive performances of C-path and G-path gates via weak XKNLs, the qubus beams, the QND (PNR) measurements, and feed-forwards, as described in Section 2. The total error probability of the single CU gate is 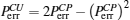
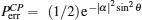
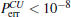
In Fig. 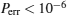
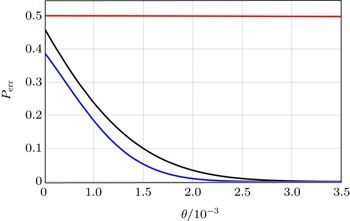 | Fig. 5. Plots of the error probabilities of the C-path gates based on coherent state and X-homodyne (red line(upper)),[23] CSS and P-homodyne (black curve (middle)),[27] and the qubus beams and the QND (PNR) detection (blue curve (lower)), each as a function of θ (the XKNL’s phase shift), for probe beam amplitude α = 1000. The red (upper), black (middle), and blue (lower) plots are the functions of  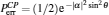 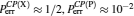 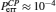 |
In experimental implementation of multi-qubit gates, the fidelity of multi-qubit gates[17–27] with using the homodyne measurement strategy will be reduced,[28–31] owing to the photon loss-related decoherence. However, the proposed CU gate can reduce the decoherence by increasing the coherent state amplitude and using the PNR measurements.[28–38] Furthermore, our CU gate based on the qubus beams does not need to perform the displacement operator D(− α), and XKNL (coupling phase shift) of −θ.[33–38] The minus conditional phase shift in XKNL is known to be difficult to implement practically.[55] Another advantage of the devised CU gate, which is composed of consecutive operations of C-path and G-path, is that the qubus beam |α〉a that is employed in the C-path gate can be recycled (|α〉a or |α cosθ〉a) in the G-path gate. In practice, the strength of the XKNL can be amplified by using EIT,[53,54] whispering-gallery mode micro-resonators,[56,57] optical fibers,[58] and cavity QED.[59,60] These methods can also reduce the absorption or losses of signal photons and the probe beam (coherent state) under a weak XKNL (θ ≪ 1). Moreover, references [61] and [62] show the feasibility of the large nonlocal nonlinear interactions in a Rydberg EIT system. For generating a large XKNL between co-propagating weak pulses in 87Rb, Wang et al.[63] proposed the use of double EIT. Thus, the sufficient strength of the XKNL for optical QIP is expected in the implementation of the realization.
Consequently, the proposed CU gate, in which used are the weak XKNLs, two qubus beams, QND (PNR) measurements and feed-forwards, is almost deterministic with 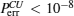
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 | |
| 63 |