For quantum information, the interference occupies the core technology. Many novel protocols and schemes rely upon high-visibility interference of photons, such as quantum cryptography,^[1] quantum teleportation,^[2] quantum repeaters^[3] or linear optics quantum computing.^[4] Interference originates from indistinguishableness. For high visibility, the interfering pulses should be indistinguishable in all possible degrees of freedom.^[5–9]

The quantum key distribution (QKD) has been paid much attention since 1984.^[10–13] Instead of the single-photon source, WCPs play a key role in practical QKD, based on the decoy-state technique.^[14,15] Recently, measurement-device-independent (MDI) QKD, promising immunity against all detector attacks, attracts much attention^[16–20] This protocol requires decoy states and phase randomization for the practical safety. Meanwhile, high visibility HOM-type interference between two WCPs is essential to the MDI QKD experiments.^[16,21]

The HOM interference with independent coherent pulses is usually treated as classical interference, hence it is described in classical electromagnetic waves superposition theory^[6,22,23] before. In this work, we describe this kind of interference clearly based on quantum optics, which aims to offer more details and useful information to applications like QKD. In Section 2, analysis results confirm the maximum HOM interference visibility of 50%^[6] for independent WCPs. As the averaged photon number of WCPs increases, the HOM interference visibility will decrease. Moreover, we conclude that the maximum visibility of dip is contributed by the single-photon states of the two WCPs, without considering the noise. With the detector’ dark count noise (the main noise), the visibility of dip will decrease from 50% to 0 when the average photon number of WCPs is small enough. Meanwhile, the dip mainly comes from those single-photon states.

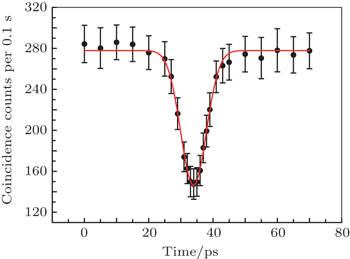
To verify the theoretical analyses, we experimentally demonstrate the HOM interference between two WCPs in Section 3. Different from MDI QKD experiments^[16,21] that use two laser sources, our two interfering pulses are split from single WCP with a temporal full width of 50 ps (FWHM, full width at half maximum). To imitate the uniform phase randomization, we scan the relative phase of the interfering WCPs by applying triangular wave to the phase modulator. It is worth to mention that our phase modulation setup is designed to be polarization insensitive.^[24,25] Finally, we obtain a fitting two-pulse interference visibility of 52.57%, very close to the theoretical value 50%, see Section 3. This result confirms our theoretical analyses. The two-pulse coherence time (FWHM) is 9.3 ps. Since the equivalent phase randomization is immune to slow phase fluctuations of either the phase modulator or transmission channels, our experiment setup can provide a simple and stable method of distance sensing on the level of picosecond. Furthermore, we propose a new experiment design using two Faraday mirrors. This design avoids using any active phase modulation and polarization control, and it promises higher resolution.

Figure 1 shows the HOM-type interference between two independent WCPs. Here, “independent” means that the relative phase of WCPs is uniformly and randomly distributed within 0 ∼ 2π. These two pulses with the same wavelength and polarization are combined by a 50/50 BS. And their states can be expressed by the creation and annihilation operators.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The drawing of principle of weak coherent state HOM interference. BS: beam splitter.

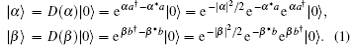
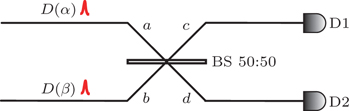
It is the essence of the two-pulse interference that the detectors can not distinguish the two cases above. To demonstrate this viewpoint, we will depict the two-pulse interference progress with the creation and annihilation operators.

Before reaching BS, the initial state can be expressed as

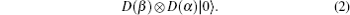
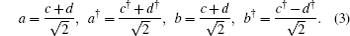
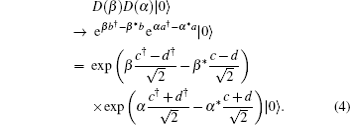
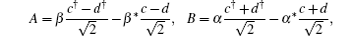
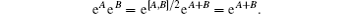
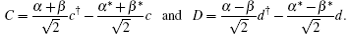
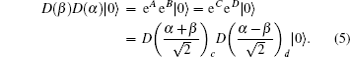
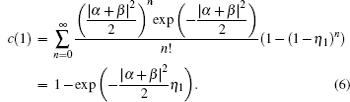
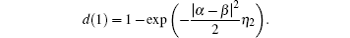
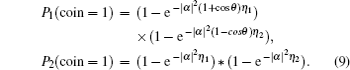
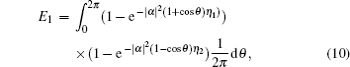
Since the formulation of E₁ is complex, here we give some numerical integrations. As depicted in Fig. 2, when η₁ or η₂ are fixed, dip achieves the maximum when η₁ = η₂. And the lower the detection efficiencies (≠ 0) are, the closer to the maximum value 50% dip is. We also calculate dip under different average photon numbers. As depicted in Fig. 3, dip approaches the maximum (50%) as |α|² approaches zero. Fig. 2.

dip versus the detection efficiencies. |α|² = |β|² = 1.

Fig. 3.

dip versus the average photon number |α|² = |β|². η₁ = η₂ = 10%.

Now we prove that the maximum visibility of 50% comes from the two-photon HOM interference. In terms of the number state, the initial state of the two interfering WCPs can also be expressed as

where |m〉 (|n〉) denotes the m-photon (n-photon) state, and the term e^{−(|α|2+|β|2)}αβ|1〉_a|1〉_b can be treated as the two-photon interference. For this term of the two-photon interference, the coincidence probability is zero in case of no temporal misalignment. While, with the temporal misalignment out of coherence time (non-interference), the coincidence probability produced by the two single-photon states |1〉_a|1〉_b is

From Eq. (13), we obtain E₂ = E + A, where A denotes the coincidence probability produced by all other terms of Eq. (13) except e^{−(|α|2+|β|2)}αβ|1〉_a|1〉_b, under no interference. So, the visibility of dip contributed by the term |1〉_a|1〉_b is

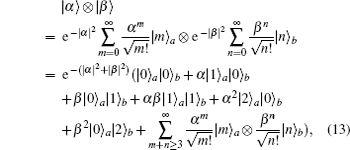
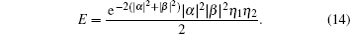
With |α|² = |β|², we have

Numerical calculations give and

see the blue and yellow curves in Fig. 4. Then we obtain

Hence, the maximum visibility of 50% all comes from the single-photon states in WCPs. And as |α|² approaches zero, dip′ increases fast, see the yellow curve in Fig. 4. The phase randomization plays a key role in this process for two reasons. First, the two-photon interference results have no relation with the relative phase θ of the two WCPs as shown in Eqs. (14) and (15), thus the phase randomization does not change dip′. Second, the phase randomization makes the dip caused by the other terms in Eq. (13) except |1〉_a|1〉_b be zero. When θ varies from 0 to 2π, the maximum visibility of dip can cover the range from 0% to 100%. Of course, dip in Eq. (12) can be treated as the average value of the visibility of dip with the fixed phase uniformly distributed within 0 ∼ 2π. Interestingly, we can not judge whether the relative phase θ is uniformly randomized or fixed at π/4 by the maximum visibility of 50%, see the green and blue curves in Fig. 4. In the latter case, the maximum visibility of dip (50%) also comes from two-photon interference. While, compared with the fixed relative phase, the phase randomization is immune to the slow phase fluctuations introduced by external circumstances. Further more, the phase randomization is one of the requirements for the securities of decoy-state and MDI QKD protocols.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The HOM interference visibilities of dip versus the average photon number (|α|2 = |β|2). We still set η1 = η2 = 10%. Blue (green) curve: dip (dip′). Green curve: the visibility of dip with the relative phase θ between WCPs fixed at π/4.

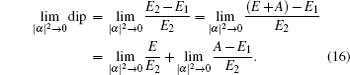
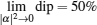
For briefness and highlighting the emphasis, the analyses above do not consider the noise, which is mainly caused by the dark counts of the single photon detectors in our experiment. We can easily obtain the result considering the dark-count noise, by adding the dark count probability to the probability of one click in c (or d) port. With the dark count probability of 10⁻⁶ (one typical value for the 1550-nm detectors), we did some numerical simulations similar to those in Figs. 2, 3, and 4. When the dark count probability is negligible compared to the average photon number, the simulation results are little different from the ones without considering the noise. While, with the average photon number less than 10⁻³ photons per pulse, dip decreases from 50% to 0% rapidly. Similarly, when the detection efficiencies approach 0, dip in Fig. 2 decreases from 50% to 0% rapidly. It is worth to mention that the simulation results still support the conclusion that dip comes from single-photon states in WCPs when the average photon number approaches 0.

Our experimental setup is shown in Fig. 5. The laser is attenuated to produce WCPs at a repetition frequency of 1 MHz. Then BS1 splits the laser into two WCPs, which are indistinguishable in the frequency domain. BS2 combines the two WCPs and the HOM interference occurs here. Two optical delayers change the temporal misalignment of these two WCPs at BS2. The delay modulation resolution of 1 fs is absolutely enough to make the two interfering WCPs, with the coherence time of around 10 ps, indistinguishable in the temporal domain. To achieve the polarization match between the two interfering WCPs at BS2, we use two PCs to minimize the count rate of D3 when the temporal misalignment is out of the coherence time. The variable attenuator is used to balance the intensities of the two interfering WCPs. Fig. 5.

The HOM interference experimental setup. The laser: 1550 nm, temporal duration time of 50 ps (FWHM). OD: optical delayers, Newport Corp. FM: Faraday mirror. PM: phase modulator. PC: polarization controller. PBS: fiber polarization beam splitter. D1, D2, and D3: single photon detectors with gate width of 1 ns. The coincidence counts are detected by D1 and D2. And their detection efficiencies are 15% and 16% respectively.

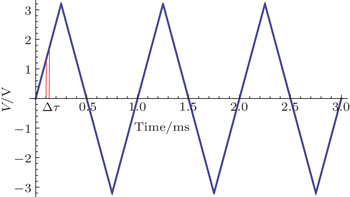
We use the PM to introduce the extra relative phase between the two interfering WCPs. The phase modulation setup, composed of FM, PM, and circulator, is polarization-insensitive.^[24–26] Since the FM can passively compensate the polarization, polarization mode dispersion, and polarization-dependent loss.^[24] For easy demonstration, we apply the triangular voltage wave to the PM to introduce uniform phase distribution within 0 ∼ 2π, rather than random uniform phase distribution. If we only concern the HOM interference visibility, the phase randomization is not necessary, see Eqs. (10) and (11).

For uniform phase distribution, there are two important points that should be satisfied. First, one phase scanning period should be much larger than the optical pulse repetition period. In our experiment, the frequency of the triangle wave is 1 kHz, as depicted in Fig. 6. And the repetition frequency of the pulse laser is 1MHz. Thus, in one period of the triangle wave, one thousand WCPs are modulated, which satisfies the first point. Second, the measurement time for the HOM interference visibility should contain enough phase scanning periods. For this point, the accumulative time for coincidence counts is up to 0.1 s, see Fig. 7. The experimental results are shown below. The count rate of D1 is 64±1 K/s under non-interference. Considering that the detection efficiency of D1 is 15%, the average photon number of each interfering WCP is estimated to be about 0.43 per pulse regardless of the loss introduced by BS2. As shown in Fig. 7, the HOM interference visibility of dip is 52.57%, close the maximum visibility of 50%. And the coherence time (FWHM) is 9.34 ps from Fig. 7.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. The triangular voltage wave applied to the PM. The peak-to-peak voltage value corresponds to the full-wave voltage (≈ 6.4 V). The frequency is 1 kHz. The laser source has a pulse repetition period of Δτ = 1 μs.

Fig. 7.

Figure Option ViewDownloadNew Window

Fig. 7. The coincidence rate between D1 and D2 versus the temporal misalignment (ps). Here we adopt the master-slave type coincidence counter. The electrical count signals of D1 are delayed by DG535 (Stanford Research systems) then trigger D2. Naturally, the count rate of D2 represents the coincidence rate. For each measured temporal misalignment, the measurement time lasts for 1 minute, which contains 600 data points.

To avoid active phase modulation and polarization control, we propose another design of setup as depicted in Fig. 8. Both WCPs splitting from the laser source will be reflected back to the BS by the FM, which passively compensates the polarization change. Note that, all WCPs in one of the interfering paths go through L-Bit delay, see Fig. 8. Here L bits corresponds to L periods of the optical pulse repetition. Commonly, L-bit delay is much longer than the coherence time. Thus the relative phase between the two interfering WCPs at BS will be randomly and uniformly distributed. Then there is no need of any active phase modulation. Moreover, the forward-backward transmissions doubles the sensitivity of the path length misalignment. Fig. 8.

The new design of experiment. L: a positive integer. 1-bit delay equals one period of the pulse repetition of the laser.

It is worth to mention that our experiment setup and the new design (especially) can tolerate slow phase fluctuations during transmissions. This provides simple and stable methods of high-resolution distance sensing, where the resolution is determined by the coherence time of the interfering WCPs.

In this work, based on quantum optics, we give detailed analyses on the HOM interference between two independent coherent pulses. Analysis results confirm that the maximum interference visibility of two independent WCPs is 50%. Additionally, we conclude that the maximum visibility of 50% comes from the single-photon states of WCPs, without considering the noise.

The experiment result supports the theoretical analyses. And we propose simple and stable designs to achieve the HOM interference of WCPs. Since the HOM interference of WCPs is immune to slow phase fluctuations, our designs can provide stable ways to achieve the high-resolution distance sensing. For example, in the experiment, the coherence time of the two interfering WCPs is only 9.34 ps, which can provide a resolution on the level of ps.

We believe our work will offer helpful guidance about the interference between two independent coherent states.