† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11374096), the Natural Science Foundation of Guangdong Province, China (Grants No. 2015A030310354), and the Project of Enhancing School with Innovation of Guangdong Ocean University (Grants Nos. GDOU2014050251 and GDOU2014050252).
We propose a scheme of quantum screening to enhance the parameter-estimation precision in open quantum systems by means of the dynamics of quantum Fisher information. The principle of quantum screening is based on an auxiliary system to inhibit the decoherence processes and erase the excited state to the ground state. By comparing the case without quantum screening, the results show that the dynamics of quantum Fisher information with quantum screening has a larger value during the evolution processes.
Quantum metrology, which investigates the ultra-precise estimation of parameters, has been widely applied in quantum precise measurement,[1–5] quantum frequency standards,[6] quantum clock synchronization,[7] single photon detections,[8,9] and so on. The main task of quantum parameter estimation is to determine the precision of a physical parameter in quantum systems. Quantum Fisher information (QFI), which can be used as measurement of probability distribution on the space of the density operators, becomes a key quantity in quantum estimation theory.[10–20] More recently, enhancing parameter precision of optimal quantum estimation by direct quantum feedback was reported.[10] The authors found that the QFI could be obviously enhanced by quantum feedback. Besides, the estimation of the quantum channel parameter for a two-qubit system with each qubit independently interacting with its Markovian environment has also been investigated.[20] The authors studied the dynamics of QFI with respect to the decoherence rate and the interaction strength. According to the quantum Cramér–Rao (QCR) inequality,[21] the value of QFI provides an upper bound on the parameter precision. Therefore, the larger QFI indicates the higher precision of the estimated parameter. At the same time, for the properties of monotonicity and convexity, QFI closely connects with other quantities such as quantum entanglement,[22,23] spin squeezing,[13] and non-Markovian effect.[14,18]
However, any realistic quantum system is open since the unavoidable interaction with its environment induced the decoherence belonging to the coupled systems. According to the styles of information flow, the time evolution of the quantum system can be divided into two classes: One is a Markovian process,[24] which means the coupling of the system and its environment is weak so that one can address the model with Born–Markov approximation. The main characteristic of the Markovian process is that the information flow is monotonic. The other is a non-Markovian process,[14,18] which has a vibration revival effect because of the strong coupling between the system and its environment.
In this work, we propose another alternative method, quantum screening,[25] to enhance the QFI of a qubit coupling with the zero temperature reservoir in a Markovian process. In the electromagnetic field theory, an electronic device is closed in the metal casing, which is connected with the zero-ground potential, that can be screened from the disturbing effects of the external electromagnetic field.[25] Inspired by the zero-ground screening scheme, we utilize an auxiliary system to erase the excited state to the ground state. We examine the parameter estimation of a dissipative qubit system by the quantum screening with the help of QFI, and demonstrate that the number of erasing events is proportional to the precision of the parameter. The results show that QFI can be enhanced by quantum screening. The effects of Rabi frequency and the number of erasing events on QFI are also considered. Besides, a reasonable physical explanation is given.
This paper is organized as follows: In Section 2, we introduce the basic knowledge of QFI and give the expressions of QFI with pure and mixed states. In Section 3, we discuss the main idea of the quantum screening effect on QFI of a dissipative qubit under critical and non-critical damping cases. Finally, we briefly summarize the paper in Section 4.
Firstly we review some basic conceptions of parameter estimation theorem and QFI which will be used in this paper. As we know, the main goal of parameter estimation is to acquire the best observable. Considering a quantum state ρ(θ), we need to estimate the observable 



The screening interferometric phase estimation method is plotted in Fig. 



We first study the dynamics of QFI without screening as shown in Fig.

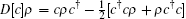



Figure



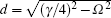




Let us now demonstrate that the screening method does enhance the parameter precision for every situation of the constants Ω. The dynamics of QFI for the output state can be compared with respect to non-screening and screening operations for a different order of the Rabi frequency Ω in Fig.
In this work, we have studied the QFI of a dissipative qubit system with and without the quantum screening, an auxiliary qubit which is erased from excited state to the ground state. We found that the case with screening can reduce the information, hence enhancing the precision measurement limit. What is more, the Rabi frequency Ω and erasing events N are two meaningful factors to affect the precision; the exact discussion and physical mechanism have been given in context.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 |





