† Corresponding author. E-mail:
Project supported by the Science and Technology Development Foundation of China Academy of Engineering Physics (Grant Nos. 2013A0201010 and 2015B0201039) and the National Natural Science Foundation of China (Grant No. 11402032).
Large-scale molecular dynamics simulations are performed to study the fragmentation of metallic liquid sheets with high velocity gradient. Dynamic fragmentation of the system involves the formation of a network of fragments due to the growth and coalescence of holes, decomposition of the network into filaments, and further breakup of the filaments into spherical clusters. The final size distribution of the fragmented clusters in the large volume limit is found to obey a bilinear exponential form, which is resulted from the heterogeneous breakup of quasi-cylindrical filaments. The main factors contributing to fragmentation heterogeneity are introduced, including strain rate inhomogeneity and matter distribution nonuniformity of fragments produced during decomposition of the network structure.
Rapid fragmentation of fluids by adiabatic expansion takes place in numerous situations. Besides the commonly observed phenomena such as the atomization of a diesel fuel, fragmentation of a metallic liquid sheet takes place in the ejection process. Ejection is a kind of dynamic phenomenon which occurs during reflection of strong shock waves from a micro-machined metal surface. [ 1 ] The interaction between the shock wave and the machined surface groove causes the generation of a microjet which expands under the velocity gradient and finally breaks up into a large number of ejecta clusters. Characterizing the size distribution of ejecta is of great importance in developing a complete ejecta source model. Despite the universal occurrence of this phenomenon, the underlying mechanisms that govern the fragmentation process and the final distribution of fragments are still not fully understood. Over the past decades, several statistical models have been developed to predict the fragment size distributions. [ 2 – 6 ] However, those models are phenomenological and unable to describe the fragmentation dynamics. Moreover, the lack of precise fragmentation models and accurate data on surface tension and viscosity of metals under extreme conditions poses great challenges to current conventional hydrodynamics approaches. [ 7 ]
In order to perform a direct numerical calculation of the fragmentation process, the method of molecular dynamics (MD) is adopted. Though the spatial and temporal scales involved in the MD simulations are several orders of magnitude smaller than those in real experiments, this method enables us to obtain the dynamic fragmentation processes without any requirement of modeling approximation as in hydrodynamic methods. Abraham et al. [ 8 ] first explored the decomposition of an unstable two-dimensional (2D) system by using MD simulations. Holian and Grady studied the fragmentation of a 2D system and compared the fragment distributions with Grady’s energy balance model. [ 9 , 10 ] Later, the fragmentation of three-dimensional (3D) liquid systems was investigated. [ 11 – 13 ] Those works give us great insights into the dynamic fragmentation behaviors of fluids at the atomistic level, and help to test various phenomenological models. However, the preceding studies concern the systems with simple Lennard–Jones pairwise potentials and the homogeneous adiabatic expansion of them. Therefore, the fragmentation of a system, described by an accurate interatomic potential, under heterogeneous expansion loading needs to be explored.
In this paper, we use large-scale MD simulations to study the fragmentation of a metallic liquid sheet which is adiabatically stretched along one direction of the system. On one hand, this model enables us to investigate the fragmentation of material described by a more accurate interatomic potential. On the other hand, the model also mimics the breakup of metallic liquid microjet generated from a shock-loaded metal with surface roughness, where the size distribution of the fragmented particles is of great importance in developing a complete ejection model. [ 14 – 17 ] Thus, the objectives of this work are to obtain the dynamic fragmentation process and the resulting fragment size distribution of the system, and to reveal the underlying mechanisms that govern the fragmentation behaviors.
We start the simulation with single crystalline copper in a thin slab geometry, consisting of 500 × 8 × 800 elementary cells in the x , y , and z axes. The widely used embedded atom model (EAM) potential proposed by Mishin et al. [ 18 ] is used to model the interactions between the copper atoms. The potential, which inherently takes into account the effects of surface tension and viscosity, can precisely reproduce the thermomechanical responses of Cu in both equilibrium and dynamic conditions.
To prepare the sheet of liquid metal, the isobaric–isothermal ensemble ( NPT ) under zero external pressure and three-dimensional periodic boundary conditions is adopted. The slab is firstly heated from 300 K to above the melting point (2000 K) during a time period of 200 ps, and further equilibrated at 2000 K for another 100 ps. Consequently, a sheet of liquid metal with dimensions of 192.4 nm× 3.08 nm× 308 nm in thermal equilibrium state is finally obtained. Then, a linear velocity gradient from 0 to 3 km/s along the x axis is imposed within the sheet during a single iteration, resulting in a strong tension effect with an instantaneous strain rate about 1.6×10 10 s −1 . Simulations of tension and fragmentation of the sheet are performed with the microcanonical ensemble ( NVE ), and the periodic boundary condition is applied only along the z axis. The Newton equation of motion is integrated by the velocity Verlet algorithm with a time step of 1 fs.
The cluster analysis methods proposed by Durand et al. [ 14 , 15 ] are adopted to investigate the size distribution of ejecta. Briefly, there are two steps in this method to identify the ejecta cluster and quantify its volume. First, the simulation space is divided into very small voxels (3D cubic cells) and the voxel containing one or more atoms is defined as atom-filled. Second, a cluster is defined as an aggregate of atom-filled voxels with distance smaller than a critical value (the nearest neighbor distance). The volume of a cluster is the total number of voxels making up the cluster.
The volume distribution of ejecta is studied by using a binning technique, where the numbers of clusters are averaged over bins of width equal to increasing powers of 2 to group the large number of fewer populated volumes. [ 19 ] Furthermore, in order to obtain good statistics in cluster size distribution, three additional simulations are performed. Each additional simulation runs from the same initial atomistic coordinates but with different Maxwellian velocities. The resulting ejecta distributions are then summed to reduce the statistical errors.
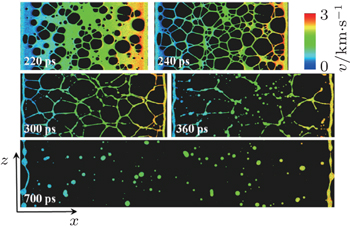
Figure
Figure
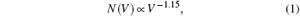
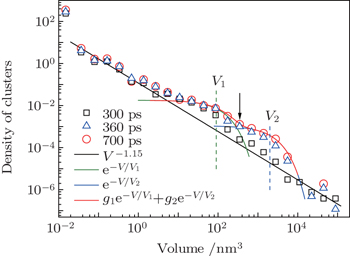
As the microsheet breaks up further, the volume distribution in the large size limit, especially for volumes larger than 100 nm 3 , changes gradually from the power law to another form (360 ps and 700 ps in Fig.
The change of volume distribution in the large size limit is related to the further breakup of bigger filaments with quasi-cylindrical shape. The breakup of the quasi-cylindrical filaments can be regarded as a 1D Poisson random partitioning process. Then, the resulting fragment volume distribution can be described by a linear exponential law. [ 20 ] In fact, in the preceding works on the fragmentation of microsheets generated from a shock-loaded metal, exponential size distributions of ejecta particles were obtained. [ 15 , 17 ] However, for the liquid sheet model in this study, unlike the linear exponential form in the previous works, the final volume distribution of fragments in the large volume region (20 nm 3 , 6000 nm 3 ) can be well fitted by a bilinear exponential function (red curve in Fig.
According to Grady and Kipp’s geometric statistical fragmentation model, [ 20 ] if fragmentation of the filaments is homogeneous, that is, all of the filaments experience a similar breakup process, the mean volume keeps constant over the whole region and the volume distribution obeys a linear exponential law. On the other hand, if heterogeneous fragmentation of filaments takes place, the average fragment volume varies within the region of consideration. Thus, the overall fragment distribution could be characterized by a bilinear exponential form
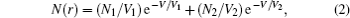
Moreover, if the fragments transform into a spherical shape, such as the fragmentation picture at 700 ps in Fig.

 | Fig. 3. The simulated histogram (black squares) and bilinear exponential fitting (red line) of the cluster radius distribution at 700 ps. Numbers of clusters with radius less than 2 nm are excluded. |
Next, we explore the origins of heterogeneous fragmentation of the metallic liquid sheet within the framework of Grady’s geometric fragmentation statistics. With respect to the final size distribution, the whole clusters can be roughly divided into two parts, the small and the large clusters (Fig.
Fragmentation of metallic liquid sheets with high velocity gradient is investigated by large-scale MD simulations. A bilinear distribution of the fragmented clusters, which reflects the heterogeneous nature of the fragmentation of microsheets, is obtained. The underlying mechanisms related to the fragments distributions are illustrated within the framework of geometric fragmentation statistics. The results demonstrate that the MD simulation not only provides a powerful tool to explore the fragmentation dynamics of fluids at atomistic level, but also can be used to verify various phenomenological fragmentation models. Furthermore, since the strain rates in the MD simulations are usually 3 or 4 orders of magnitude higher than those in experiments, more efforts are needed to check the influences of strain rates on the dynamics fragmentation process.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 |