Cite this Article
Feng Shi-Quan, Zang Hua-Ping, Wang Yong-Qiang, Cheng Xin-Lu, Yue Jin-Sheng. Ab initio investigation of photoinduced non-thermal phase transition in β -cristobalite. Chinese Physics B , 2016, 25(1): 016701  
Permissions
Ab initio investigation of photoinduced non-thermal phase transition in β -cristobalite
Feng Shi-Quan 1, †, , Zang Hua-Ping 2 , Wang Yong-Qiang 1 , Cheng Xin-Lu 3 , Yue Jin-Sheng 4
The High Pressure Research Center of Science and Technology, Zhengzhou University of Light Industry, Zhengzhou 450002, China
School of Physics and Engineering, Zhengzhou University, Zhengzhou 450002, China
Institute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China
Luoyang Sunrui Sprcial Equipment CO., LTD, Luoyang 471003, China

 

† Corresponding author. E-mail: fengsq2013@126.com

Project support by the National Natural Science Foundation of China (Grant Nos. 11374217 and 11547158).

Abstract
Abstract

Using the linear-response method, we investigate the phonon properties of β -cristobalite crystal under electronic excitation effect. We find that the transverse-acoustic phonon frequency becomes imaginary as the electron temperature is increased, which means that the lattice of β -cristobalite becomes unstable under intense laser irradiation. In addition, for the optic phonon mode, the LO(H)–TO(H) splitting disappears when the electronic temperature reaches a certain value, corresponding to the whole transverse-acoustic phonon branches becoming negative. It means that the electronic excitation destroys the macroscopic electric field of β -cristobalite. Based on the calculated phonon band structures, some thermodynamic properties are calculated as a function of temperature at different electronic temperatures. These investigations provide evidence that non-thermal melting takes place during a femtosecond pulse laser interaction with β -cristobalite.

PACS : 67.25.bd ; 63.20.dk ; 05.70.Ce
Keyword : first principles theory ; thermodynamic properties ; non-thermal melting ; electronic excitation
1. Introduction

As one of the most common natural chemical compounds on earth, silicon dioxide SiO 2 plays an important role in many technological and industrial applications. [ 1 – 5 ] Quartz, coesite, cristobalite, and tridymite are the most widely known crystalline polymorphs of silica. They are stable or metastable under ambient conditions. In addition, amorphous silica glass is also commonly discovered in natural geologic environments and applied in technology.

The radiation-induced processes of some silica mineral phases, especially the α - and β -quartz, have been widely investigated. [ 6 – 8 ] However, there are few studies about the effect of the ultra-laser radiation on cristobalite. As is well known, laser radiation on a material (natural or synthetic) gives rise to a large number of electrons transmitting from the valence band to the conduction band, and leads to heating the electrons to a high temperature (about 10 4 K) in a short time (10–100 fs). Such a high electronic temperature would modify the interatomic bond, and lead to the instability of the host lattice and then to a non-thermal phase transition.

As early as 1979, the non-thermal melting mechanism was first proposed. Van Vechten et al . [ 9 ] figured out that the diamond structure becomes unstable at excitation levels of > 9% of the valence electrons. Reitze et al . [ 10 ] employed femtosecond pump–probe techniques to investigate the melting dynamics of graphite. A high-reflectivity phase, lasting less than 10 ps, appears when the surface is photoexcited at an excitation fluence above 0.13 J/cm 2 . Using 200-fs electron pulses, Harb et al . [ 11 ] investigated the structural details of freestanding films of polycrystalline and (001)-oriented crystalline Si at a high excitation level of carriers, and found an electronically driven order-to-disorder phase transition in Si. By using femtosecond time-resolved linear and nonlinear optical spectroscopies, Sokolowski-Tinten et al . [ 12 ] investigated the laser-induced ultrafast order–disorder transitions in silicon and gallium arsenide, and found that these transitions occur on a timescale of a few hundred femtoseconds. By observing the carrier-dependent changes in the potential energy surface of InSb, Hillyard et al . [ 13 ] investigated the influence of the carrier excitation on the stability of the tetrahedrally bonded semiconductor. Their studies showed that extreme carrier densities destabilize the crystal structure and lead to non-thermal melting of InSb. In addition, theoretical investigations have found that the transverse acoustic mode of several semiconductors, [ 14 – 16 ] such as C, Si, Ge, GaAs, and InSb, becomes unstable if about more than 9% of the valence electrons are excited into the conduction band. But neither experiments nor calculations are available to find out whether cristobalite undergoes such a non-thermal melting transition as semiconductors C, Si, Ge, GaAs, and InSb [ 14 – 17 ] at the excitation levels of > 9% of the valence electrons.

Under ambient pressure, there are two phases of cristobalite, a low-temperature tetragonal form of space group P 4 1 2 1 2, the α -phase, and a high-temperature cubic form of space group F d -3 m , the β phase. The β -cristobalite as the normal product of devitrification in fused silica is stable at temperatures higher than 1470 °C. It undergoes a transition towards a metastable structure and then a reversible transition towards the α -polymorph at a temperature close to 227 °C, depending on its crystallinity and the potential presence of impurities. In this paper, we employ density functional theory to investigate the phonon properties of the β -cristobalite crystal at different electronic temperatures, and further discuss the influence of the electronic excitation effect on the lattice stability. Then according to the phonon dispersion curves, we study some thermodynamic properties under electronic excitation to find the evidence of non-thermal melting during ultra-short pulse laser interaction with β -cristobalite.

2. Computational method and technical details

There are two main methods to investigate the phonon properties in theory: the frozen-phonon method [ 18 ] and the linear-response method. [ 19 , 20 ] For the frozen-phonon approach, the force constant matrix can be obtained by perturbing the positions of the atoms slightly and calculating the reaction forces. It is necessary to use supercells of the original cell when the interatomic interaction in the system is of long range. So this method is also known as the supercell method. The main advantage of this method is that any total energy scheme can be used to evaluate the forces at a number of carefully selected distorted configurations. The original frozen phonon scheme requires a displacement with a given wave vector. The force constant matrix evaluation has been used to calculate the interplanar force constants and thus the phonon dispersion along high symmetry directions. The limit of this method is that the amount of calculation is very high. In addition, the longitudinal optic (LO)–transverse optic (TO) mode splitting cannot be directly obtained for polar crystals, and the electric field effect should be considered to amend the phonon frequency at the high-symmetry Γ point.

For the linear-response approach, the time-consuming supercell calculations are avoided. Based on the density-functional perturbation theory (DFPT), this method evaluates the dynamical matrix directly for a set of q vectors. The starting point of the linear response approach is to evaluate the second-order change in the total energy induced by atomic displacements. Its main advantage is that it has no need to artificially increase the cell size for accommodating small q vectors or for solving the long range interaction problem (force constant matrix from supercell calculations). Phonons of arbitrary wave vector can be treated. For polar crystals, the LO/TO mode splitting can be included.

In this paper, all the phonon calculations have been done with density functional theory as implemented in the open-source code ABINIT [ 21 ] within the linear-response method. We employ the Wigsen–Goedecker–Hutter pseudopotentials [ 22 ] combined with the local density approximation (LDA) [ 23 ] in our calculations. A plane-wave basis set with an energy cutoff of 25 Hrtree is chosen to ensure a stable state of the system. The electronic self-consistent function (SCF) convergence criterion is set to be 1.0 × 10 –20  Hrtree. The 2s, 2p electrons of O and 3s, 3p electrons of Si are explicitly included in the calculation. The valence electronic configurations are 3s 2 3p 4 for Si and 2s 2 2p 4 for O. In the first Brillouin zone (BZ), we sample a 6×6×6 Monkhorst–Pack grid for the β -cristobalite crystal calculations. The structural optimizations are carried out using the conjugate gradient (CG) algorithm. In addition, due to the fact that the electron at high electronic temperature will occupy the high energy band, we should carefully select the bands in our calculations. In this work, the band number is set to be 30. The optimized lattice parameter in our calculation for the face-centered cubic β -cristobalite crystal is 7.465 Å, while the experimental lattice parameter is 7.160 Å. Our calculation overestimates it by 4.3%. On the basis of our calculated lattice parameter, the phonon dispersion curves of the β -cristobalite crystal at different electronic temperatures are obtained. By setting the discrete broadening parameter, different electronic temperatures are added to different systems.

Based on the phonon properties, the thermodynamic functions can be calculated by summating phonon eigenstates labeled with phonon wave vector q and phonon mode l . These thermodynamic functions, such as the Helmholtz free energy, the internal energy, the constant-volume specific heat, and the entropy, as a function of temperature, can be obtained with the phonon frequency ω = ω ( q , l ). We can express the Helmholtz free energy F , the internal energy E , the entropy S , and the constant-volume specific heat C V as

where n and N are the number of atoms per primitive unit cell and the number of primitive unit cells, respectively; g ( ω ) is the phonon density of states, which satisfies the normalizing condition; and k B and h are the Boltzmann constant and the Planck constant, respectively. The phonon frequency ω = ω ( q , l ) changes as the electronic temperature is elevated, the above thermodynamic functions would be influenced by the electronic excitation effect. In this paper, we investigate these thermodynamic functions at different electronic temperatures.

3. Result and discussion
3.1. Lattice parameter of β -cristobalite crystal under intense laser irradiation

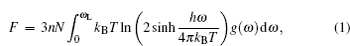
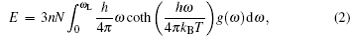
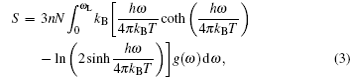
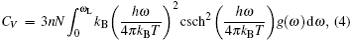
To investigate the lattice parameter of the β -cristobalite crystal under intense laser irradiation, we optimize the β -cristobalite lattice at different electronic temperatures. The dependence of the lattice parameter on electronic temperature T e for the face-centered cubic (fcc) β -cristobalite crystal is shown in Fig.  1 .

Fig. 1. Lattice parameter of β -cristobalite as a function of electronic temperature.

From Fig.  1 , it can be seen that the face-centered cubic lattice of β -cristobalite expands as the electronic temperature is elevated. As is well known, the valence electrons of a semiconductor would be excited into the conduction band when the semiconductor is irradiated by intense laser pulse. It follows the attractive bonding interaction between the atoms is destroyed while the repulsive interaction is almost not affected by the excited electron. The crystal is no longer in mechanical equilibrium at the lattice constant a 0 , and would expand to have a new equilibrium lattice constant a ( T e ) > a 0 . With the increase of the electronic temperature, more and more valence electrons are excited, and the attractive bonding interaction between atoms would be further weakened. Then the strength of the repulsive force between atoms grows, and the equilibrium lattice constant increases. This result is very similar to the theoretical result obtained by Shokeen and Schelling [ 24 ] for semiconductor Si and the experimental results [ 25 , 26 ] obtained by using pulsed lasers to induce disordered crystalline Si surfaces.

3.2. Lattice dynamical properties of β -cristobalite crystal under intense laser irradiation

For the β -cristobalite crystal, there are 6 atoms (2 Si atoms and 4 O atoms) in a primitive unit cell. So the complete phonon band structure consists of 18 phonon dispersion curves. There are 3 acoustic branches corresponding to sound propagation as q → 0 and 15 optic branches.

Figure  2 shows our calculated phonon dispersion curves of fcc β -cristobalite at different electronic temperatures. It is noted that all the phonon frequencies decrease with the increase of electronic temperature T e . For the acoustic modes, we find that the phonon frequencies of the two lower transverse acoustic (TA) branches entirely become imaginary when the electronic temperature is raised to 2.0 eV. It indicates that the softening of the transverse-acoustic phonons is due to the thermal excitation of the electrons. The complete transverse acoustic branch becoming imaginary is a clear signature of lattice instability induced by the thermal electronic excitation. The critical electronic temperature of the complete transverse acoustic branch becoming imaginary for fcc β -cristobalite is between 1.5 eV and 2.0 eV. Similar studies [ 16 , 27 , 28 ] have been conducted for semiconductors Si, C, Ge, InSb, and GaAs, and similar results have been obtained for them.

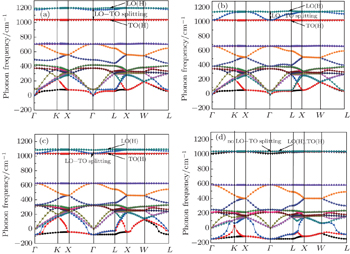Fig. 2. Phonon band structures of β -cristobalite crystal at different electronic temperatures: (a) T e = 0 eV, (b) T e = 1.0 eV, (c) T e = 1.5 eV, (d) T e = 2.0 eV.

As is well known, for the ionic crystal, an LO–TO splitting exists at the center of the Brillouin zone due to the removal of degeneracy between TO and LO phonons. The LO–TO splitting also exists at the high-symmetry Γ point of zone-center wave vector for atomic crystal β -cristobalite. As a polar material, the face-centered cubic structural β -cristobalite crystal also has a macroscopic electric field induced by the polar distribution of molecular charge. This electric field affects the LO phonons in the limit q → 0, breaking the degeneracy of the LO mode with the TO mode. So there also exists an LO–TO splitting in the face-centered cubic structural β -cristobalite crystal at the Γ point. For the β -cristobalite primitive unit cell, there are 15 optic branches (includes 5 LO modes and 10 TO modes). In theory, there are 5 LO–TO splittings. For convenience, we divide them into three parts. For the optic branches with frequencies larger than 1000 cm –1 , we call them high frequency optic modes, while the optic branches with frequencies of 500–800 cm –1 and 0–400 cm –1 are called moderate and low frequency optic modes, respectively. In this paper, we merely discuss the LO–TO splitting for high frequency optic modes, and call it LO(H)–TO(H) splitting. As is well known, the LO–TO splitting is an important parameter to evaluate the strength of ionicity for ionic crystals, while the LO(H)–TO(H) splitting can be used to measure the strength of molecular polarity for an atomic crystal. [ 29 ] In Fig.  2 , we mark the LO(H)–TO(H) splitting on the phonon dispersion curves at different electronic temperatures. It can be easily observed that the LO(H)–TO(H) splitting of the β -cristobalite crystal decreases with the increase of the electronic temperature. When the electronic temperature reaches a certain critical value, the LO(H)–TO(H) splitting disappears. For the β -cristobalite crystal, this value is just the electronic temperature corresponding to the whole TO branches becoming negative. It means that the instability of the structure destroys the macroscopic electric field in the β -cristobalite crystal, and leads to the disappearance of the LO(H)–TO(H) splitting.

Another interesting phenomenon can be easily seen in Fig.  2 . From the phonon dispersion curves at 0 eV in Fig.  2(a) , we can see that there are three gaps for the optic modes. When the electronic excitation effect is considered, the gap of high frequency optic modes and the gap of low frequency optic modes disappear. But the gap between high and moderate frequency optic modes still exists, and it increases as the electronic temperature increases. In addition, the frequencies of the optic modes decrease as the electronic temperature increases, and approach asymptotically towards some limit values. For the high frequency optic branches, this limit value is about 1000 cm –1 , while the top of the moderate frequency optic branches approaches about 600 cm –1 and the boundary between moderate and low frequency optic branches is broken down.

3.3. Thermodynamic properties of β -cristobalite crystal under intense laser irradiation

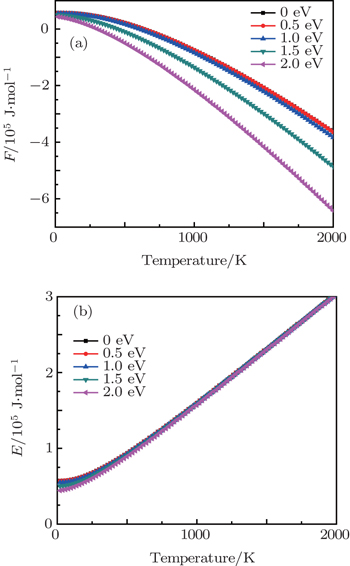Based on the investigation of the phonon dispersion relationship, the temperature-dependent phonon contributions to the Helmholtz free energy F and the internal energy E at different electronic temperatures are calculated and shown in Fig.  3 . From Fig.  3 , it can be seen that the phonon free energies at different electronic temperatures increase as the temperature increases. In addition, the phonon free energy–temperature curves move down with the increase of the electronic temperature. For the phonon internal energy E , the elevated electronic temperature has a significant effect on it when the lattice temperature is low, while the electronic excitation effect can almost be ignored when the lattice temperature is higher than 500 K.

Fig. 3. (a) Phonon contributions to Helmholtz free energy F and (b) internal energy E of β -cristobalite crystal at electronic temperatures from 0 to 2.0 eV.

Figure  4 shows the variations of phonon entropy S and phonon heat capacity C V with temperature of the β -cristobalite crystal at different electronic temperatures. It can be seen that the phonon entropy S , as a measure of the uncertainty associated with a random variable for the material system, increases with increasing temperature at different electronic temperatures. In addition, the phonon entropy–temperature curve moves upward with increasing electronic temperature, which means that randomness of the target system goes up with the enhancement of the electronic excitation effect. A significant increase in the phonon entropy–temperature curve from T e = 1.0 eV to 1.5 eV is apparent in Fig.  4(a) . This result may be an indication of the β -cristobalite crystal undergoing a phase transition from solid to liquid. From the variation of the phonon dispersion relationship of the β -cristobalite crystal between T e = 1.0 eV and 1.5 eV, we can see that the transverse acoustic phonon frequencies begin to become imaginary, which means that the non-thermal melting is taking place. But it is different from the result obtained for the zinc-blende structure InSb in our previous investigation. [ 30 ] For InSb, there exists a critical value, if the electronic temperature exceeds this value, the phonon entropy–temperature curve would basically remain unchanged. For the β -cristobalite crystal, there also exists a critical electronic temperature at which a significant increase in the phonon entropy–temperature curve occurs, but if we further increase the electronic temperature, the phonon entropy–temperature curve would still dramatically change. This phenomenon shows that the non-thermal melting of InSb may be a simple solid–liquid phase transition, while the non-thermal melting of the β -cristobalite crystal is a much more complicated process. In this process, the ordered structure of the β -cristobalite crystal transforms into a disordered one. What is more, the amorphous structure and the macroscopic electric field disappear in the disordered structure and then lead to the disappearance of the LO(H)–TO(H) splitting.

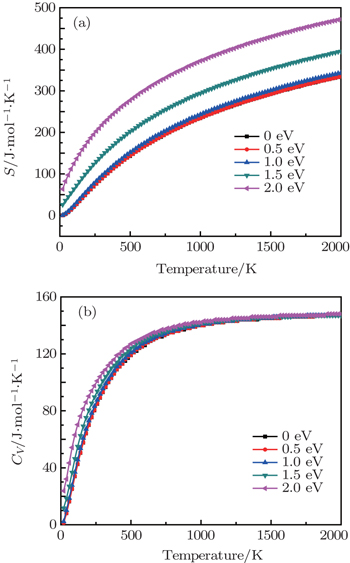Fig. 4. Variations of (a) phonon entropy S and (b) phonon heat capacity C V with temperature of β -cristobalite crystal at different electronic temperatures from 0 to 2.0 eV.

From Fig.  4(b) , it can be seen that the electronic excitation has a remarkable influence on the phonon heat capacity at low lattice temperature. While when the lattice temperature reaches 1000 K, the electronic temperature almost has no influence on the phonon heat capacity. In this range of temperatures, the electronic excitation effect has almost no influence on the phonon heat capacity. This result suggests that the two-temperature model is reasonable for simulating the interaction process between ultra-fast laser and β -cristobalite at high temperature.

4. Conclusion

We employ the density functional theory to investigate the lattice parameter, phonon band structure, and thermodynamics properties of the β -cristobalite crystal under electronic excitation. The results show that the lattice of the β -cristobalite crystal expands as the electronic temperature is elevated. A variety of anomalies are observed in the phonon dispersion curves at high electronic temperatures. The LO(H)–TO(H) splitting of the β -cristobalite crystal decreases with the increase of the electronic temperature, and it disappears when the electronic temperature T e reaches 2.0 eV. It means that the instability of the structure destroys the macroscopic electric field in the crystal. The disappearance of the macroscopic electric field may mean that the order structure of the β -cristobalite crystal transforms into a disordered one. In addition, based on the phonon properties, the thermodynamic properties of the β -cristobalite crystal are calculated as a function of temperature at different electronic temperatures. A significant increase is observed in the phonon entropy–temperature curve in the electronic temperature range from T e = 1.0 eV to 1.5 eV. It corresponds to the variation of the phonon dispersion relationship of the β -cristobalite crystal between T e = 1.0 eV and 1.5 eV. So it can be considered as an indication of the phase transition from order to disorder in the β -cristobalite crystal.

Reference
1 Ling Y M Wu S E 2005 Rev. Sci. Instrum. 76 126107
2 Correcher V Garcia-Guinea J Sanchez-Munoz L Delgado A 2003 J. Mater. Process. Tech. 143 871
3 Beerten K Stesmans A 2006 Appl. Radiat. Isotopes. 64 594
4 Skuja L Hirano M Hosono H Kajihara K 2005 Phys. Stat. Sol. 2 15
5 Lieb K P Keinonen J 2006 Contemp. Phys. 47 305
6 Hashimoto T Notoya S Arimura T Konishi M 1996 Radiat. Meas. 26 233
7 Ogoh K Takaki S Yamanaka C Ikeya M Ito E 1996 J. Phys. Soc. Jpn. 65 844
8 Correcher V Molina D Garcia-Guinea 2003 J. Rev. Mex. Fis. 49 235
9 Van Vechten J A Tsu R Saris F W 1979 Phys. Lett. A 74 422
10 Reitze D H Wang X Ahn H Downer M C 1989 Phys. Rev. B 40 11986
11 Harb M Ernstorfer R Hebeisen C T Sciaini G Peng W Dartigalongue T Eriksson M A Lagally M G Kruglik S G Miller R J D 2008 Phys. Rev. Lett. 100 155504
12 Sokolowski-Tinten K Bialkowski J von der Linde D 1995 Phys. Rev. B 51 14186
13 Hillyard P B Gaffney K J Lindenberg AM Engemann S Akre R A Arthur J Blome C Bucksbaum P H Cavalieri A L Deb A Falcone R W Fritz D M Fuoss P H Hajdu J Krejcik P Larsson J Lee S H Meyer D A Nelson A J Pahl R Reis D A Rudati J Siddons D P Sokolowski-Tinten K von der Linde D Hastings J B 2007 Phys. Rev. Lett. 98 125501
14 Stampfli P Bennemann K H 1995 Appl. Phys. A 60 191
15 Zijlstra E S Tatarinova L L Garcia M E 2008 Phys. Rev. Lett. 101 135701
16 Feng S Q Zhao J L Cheng X L 2013 J. Appl. Phys. 113 023301
17 Hillyard P B Reis D A Gaffney K J 2008 Phys. Rev. B 77 195213
18 Kunc K Martin R M 1982 Phys. Rev. Lett. 48 406
19 Giannozzi P Gironcoli S Pavone P Baroni S 1991 Phys. Rev. B 43 7231
20 Gonze X Lee C 1997 Phys. Rev. B 55 10355
21 Gonze X Beuken J M Caracas R Detraux F Fuchs M Rignanese G M Sindic L Verstraete M Zerah G Joller F Torrent M Roy A Mikami M Ghosez P h Raty J Y Allan D C 2002 Comput. Mater. Sci. 25 478
22 Hartwigsen C Goedecker S Hutter J 1998 Phys. Rev. B 58 3641
23 Kohn W Sham L J 1965 Phys. Rev. 140 A1133
24 Shokeen L Schelling P K 2010 Appl. Phys. Lett. 97 151907
25 Thompson M O Galvin G J Mayer J W Peercy P S Poate J M Jacobson D C Cullis A G Chew N G 1984 Phys. Rev. Lett. 52 2360
26 Poate J M Brown W L 1982 Phys. Today 35 24
27 Recoules V Clerouin J Zerah G Anglade P M Mazevet S 2006 Phys. Rev. Lett. 96 055503
28 Wang M M Gao T Yu Y Zeng X W 2012 Eur. Phys. J. Appl. Phys. 57 10104
29 Wang Y Wang J J Wang W Y Mei Z G Shang S L Chen L Q Liu Z K 2010 J. Phys.: Condens. Matter 22 202201
30 Feng S Q Zhao J L Cheng X L Zhang H 2013 J. Appl. Phys. 114 043519