† All authors have equal contributions.
‡ Corresponding author. E-mail:
Project supported by the Natural Science Foundation of China (Grant Nos. 21190040, 11174105, 91225114, 91430217, and 11305176) and Jilin Province Youth Foundation, China (Grant No. 20150520082JH).
In this review, we explore the physical mechanisms of biological processes such as protein folding and recognition, ligand binding, and systems biology, including cell cycle, stem cell, cancer, evolution, ecology, and neural networks. Our approach is based on the landscape and flux theory for nonequilibrium dynamical systems. This theory provides a unifying principle and foundation for investigating the underlying mechanisms and physical quantification of biological systems.
Biological systems are typically complex nonequilibrium systems across many scales, ranging from the function and recognition of proteins, [ 1 – 7 ] to the cellular networks of macromolecular complexes and regulatory pathways, [ 8 – 21 ] and even the populations of organisms. [ 22 – 24 ] A biological system usually consists of a complex network of components working together to perform specific functions shaped by evolution. The function of a biological system resides not only in the individual components, but also, more importantly, in their interactions and collective behaviors. The challenge is how to explore the complex dynamics of nonequilibrium biological systems and uncover the underlying physical mechanisms. Various experimental, theoretical, and computational approaches have been developed to meet the challenge. [ 9 – 21 , 23 – 39 ]
Physical and mathematical modeling of biological systems can give a quantitative description of the dynamical behavior of biological processes. [ 3 – 5 , 8 – 11 ] It complements intuitive observations and limited resolutions of experimental investigations. Ordinary differential equations can be used to model the deterministic dynamics of biological systems. For a system under the influence of stochastic fluctuations, which is typically the case for biological systems, Langevin and Fokker–Planck equations are usually able to reasonably describe the system’s stochastic dynamics. [ 8 – 11 , 40 – 43 ] With appropriate tools of statistical mechanics, the energy landscape theory offers a quantitative global approach to investigate the structure, function, and behavior of biological systems. Quantitative results and predictions from the energy landscape theory have been confirmed by both laboratory experiments and detailed simulations. [ 1 – 8 ] The landscape and flux theory, as a further development and an important extension of the energy landscape theory, brings out the indispensable role of the curl flux in nonequilibrium systems complementary to the potential landscape, which facilitates the unveiling of fundamental principles and physical mechanisms governing nonequilibrium biological systems with complex behaviors and varied functions across multiple scales.
On the molecular scale, the puzzle of how a denatured protein refolds to its native state (the Levinthal’s paradox [ 44 ] ) has been resolved by the funnel-like energy landscape. [ 1 – 7 ] The concept of funneled energy landscapes goes beyond the folding of protein monomers. Binding processes of biomolecules also have funneled landscapes whose topographies determine the binding mechanisms. [ 2 , 45 – 47 ] Protein folding can be regarded as a diffusion process on the energy landscape which eventually reaches the native state. As a result, the folding thermodynamics and kinetics can be inferred from the knowledge of the energy landscape. The energy landscape theory has been been further extended and applied to protein binding and conformational dynamics. [ 26 , 48 – 50 ] Significant progresses have been made on interpreting the results from the energy landscape perspectives. [ 51 – 53 ] Hence, the energy landscape theory gives a quantitative description with physical insights into the dynamics at the molecular level and has enhanced our knowledge of the corresponding biological processes.
In order to have a concrete understanding of the en-ergy landscape concept, we have used molecular dynamics simulations and equilibrium statistical mechanics to quantify the energy landscape of protein folding and binding dynamics. [ 29 , 54 , 55 ] The connections between theories and experiments have been established with quantified energy landscapes. We have explored a wide variety of models based on the energy landscape theory to investigate various biomolecular dynamics, including multi-domain protein folding, [ 56 ] intrinsically disordered proteins’ (IDPs’) binding–folding, [ 57 – 62 ] and protein conformational changes. [ 63 – 68 ] The simulation results are consistent with the experiments in many ways, identifying the critical role of the energy landscape in biological processes.
Further, the energy landscape theory allows us to use bioinformatics input to learn the rules of energetic interactions that govern protein folding and ligand binding. The energy landscape theory has been used to quantify not only the affinity but also the specificity for molecular recognition critical for drug discovery. [ 26 , 28 , 69 – 71 ] Protein structures and binding complexes have been predicted successfully using optimized energy functions based on the energy landscape theory. [ 26 , 28 , 30 – 38 , 69 – 71 ]
At the scales encompassed by systems biology, research on the dynamics, function, and stability of nonequilibrium biological networks has progressed. [ 9 – 19 , 23 , 24 , 39 – 41 , 72 – 78 ] In particular, the landscape and flux theory, which we have developed and applied to explore a variety of biological systems, is our contribution to the advancement of this field. [ 9 – 19 , 23 , 24 , 39 ] The general theoretical framework of landscape and flux consists of several components inherently interlinked by the central idea of the driving force decomposition for nonequilibrium dynamical systems. We have discovered that, in contrast to the equilibrium dynamics of biological systems determined only by the potential landscape, there are two essential parts that constitute the driving force of nonequilibrium biological systems: the gradient potential force and the curl flux force. More specifically, the potential here means the nonequilibrium potential landscape quantifiable via the steady-state probability distribution, and the flux refers to the steady-state probability flux, a signature of detailed balance breaking that indicates the system’s nonequilibrium feature in the steady state. Both parts are required to give a complete characterization of the nonequilibrium dynamics of biological systems. Based on the driving force decomposition, other components in the landscape and flux framework, including the nonequilibrium thermodynamics, the fluctuation–dissipation theorem, the fluctuation theorem, the gauge field, and the path integral with kinetic paths and rates, become integral parts of a coherent theoretical framework.
We have applied the general landscape and flux framework to investigate a wide range of more specific nonequilibrium systems with biological significance. [ 9 – 12 , 14 , 16 , 18 , 19 , 22 – 24 , 39 ] In the investigation of the cell cycle process, cell cycle phases and cell cycle checkpoints have been identified, respectively, as the local attractor basins on the landscape and the transition states between them, along the path of cell cycle oscillation. [ 9 – 11 ] The Waddington landscape and path for stem cell development, differentiation, and reprogramming have been quantified in the landscape and flux framework. [ 12 , 14 , 16 , 18 , 19 ] Cancer has been proposed to be a disease of cellular states associated with the underlying gene regulatory network, where the multiple cellular states are identified as the attractor basins on the landscape; we have studied the transitions between the normal state and the cancer state quantitatively. [ 39 ] From the perspective of the landscape and flux theory, evolution dynamics that goes beyond Wright and Fisher has been formulated and the red queen phenomennon has been explained. [ 23 ] Ecosystems have also been investigated in the landscape and flux framework, with the global stability of ecological systems quantified. [ 22 ] Neural networks with asymmetrical connections have been studied for learning and memory. [ 24 ] In addition, the non-adiabatic dynamics of gene expression, [ 17 ] self regulating genes, [ 17 , 79 ] chaotic strange attractor, [ 80 ] and spacial development with pattern formation [ 81 – 84 ] have also been explored.
The rest of this article is structured as follows. In Section 2, we discuss the folding, binding, and conformational dynamics of biomolecules in the framework of the energy landscape. In Section 3, we address the intrinsic specificity and kinetic specificity for ligand binding as well as their applications in drug discovery and design in the context of the energy landscape theory. In Section 4, we review the general theoretical framework of landscape and flux and explore its more specific applications in cell cycle, stem cell, cancer, evolution, ecology, and neural networks. The conclusion is given in Section 5.
Although the concept of an energy landscape is widespread, researchers in the field of molecular biology often use the energy landscape theory in a qualitative way. This is mainly due to the fact that the energy landscape, reflecting the delicate relationship of energy, entropy, and structural information, cannot be explicitly measured by experiments. On the other hand, experimental measurements, such as the thermodynamic temperature and kinetic rate, cannot be well predicted by theories. Consequently, the relationship between the topography of the energy landscape and the thermodynamics and kinetics of biomolecular dynamics is ambiguous. To meet the challenge, molecular simulation is proposed to serve as the meeting point, aiming to bridge the gap between theories and experiments.
Conventionally, molecular simulations are often performed under constant temperature, corresponding to the canonical ensemble. However, the energy landscape, which reflects the underlying intrinsic interactions of the system, is not supposed to be dependent on temperature explicitly. Therefore, one has to transform the temperaturedependent distribution of energies from the canonical ensemble ( n ( E , T )) into the micro-canonical ensemble ( n ( E )). This can be done using the Boltzmann relation n ( E ) ∼ n ( E , T ) e E / k B T , as encoded in the weighted histogram analysis method (WHAM). [ 85 ] The distribution of the micro-canonical ensemble, referring to the density of states, corresponds to the intrinsic energy landscape.
In theories, there are three quantities describing the topography of the energy landscape: [ 2 , 4 , 5 , 45 ] energy gap δ E between the native state and the average of non-native states, measuring the slope of the funnel; [ 86 , 87 ] energy roughness Δ E , quantifying the bumpiness of the funnel; entropy S , describing the size of the funnel. These three quantities result in a dimensionless ratio Λ , expressed as the energy gap versus energy roughness and entropy 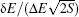
We quantified the intrinsic energy landscapes of protein folding and presented the quantitative funnel diagrams. [ 54 ] The relationship of energy, entropy, and structure can be illustrated quantitatively from the energy landscapes (Fig.
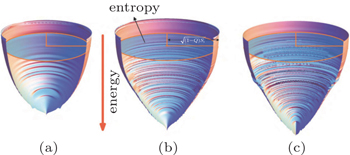 | Fig. 1. Quantitative illustrations of protein folding funnels for (a) villin headpiece, (b) CI2, and (c) P13 from simulations. The Z axis is energy. The area of each ellipsoid stratum represents entropy. The semimajor axis of the ellipsoid at each stratum is 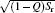 |
We found that the energy landscape topography Λ has a strong positive correlation with the thermodynamic stability (versus glass trapping) and kinetic rate. In other words, a more funneled energy landscape leads to more stable folding and a faster rate. Thus we have established the quantitative relationship between an energy landscape and folding thermodynamics and kinetics.
We then quantified the energy landscapes of protein binding. [ 29 ] For flexible biomolecular recognition, the central issue that needs to be addressed is the binding mechanism. We picked out 15 different homodimers and classified them into two groups based on different binding mechanisms found by experiments: 2-state “coupled binding–folding” homodimers and 3-state “folding prior to binding” homodimers. By quantifying the individual binding, folding, and global binding–folding energy landscapes (Fig.
 | Fig. 2. Energy landscape quantifications during flexible recognition for (a) 2-state and (b) 3-state homodimers. Each homodimer has two individual monomeric folding energy landscapes, one individual interfacial binding energy landscape, and a combined global binding–folding energy landscape. The funnel plot details are the same as Fig. |
By calculating the global binding–folding energy landscape topography Λ global , we found that Λ global is strongly correlated with the thermodynamics and kinetics of protein binding, similar to the situation in protein folding. Our findings show that the energy landscape controls the pathway, thermodynamic feasibility, and kinetic efficiency of protein to realize its function.
Using molecular simulations, we demonstrated the crucial role of the energy landscape in biomolecular dynamics. The thermodynamics and kinetics of protein folding and binding can be predicted well with the quantified energy landscape due to the strong correlation between them. On the other hand, with experimental measurements on thermodynamics and kinetics, the energy landscape can be portrayed accurately. These results bridge the gap between theories and experiments, providing a novel way to understand the biomolecular dynamics by combining the results from both theories and experiments.
The long-standing paradigm that a biomolecular function is determined by a unique folded structure is challenged by intrinsically disordered proteins (IDPs). [ 89 – 91 ] An IDP lacks a unique tertiary structure in an isolated state, either entirely or in parts, but often folds upon binding to its partners. [ 92 , 93 ] This “binding induced folding” scenario gives IDPs many advantages, [ 94 , 95 ] including fast association/disssociation rate, multiple binding targets, low affinity but high specificity, etc, resulting in IDPs’ presence in many critical cellular activities, such as transcription, signaling, and regulation. [ 96 – 98 ] Understanding IDPs’ binding–folding will refresh our view on protein folding and contributes to our knowledge of molecular biology.
The structure-based model (SBM) is a simplified molecular simulation model, derived from the energy landscape theory. [ 99 ] The SBM only takes into account native interactions, leading to a perfect funneled energy landscape. The validity of SBM is supported by the “principle of minimal frustration” indicating that the native structural topography controls the folding mechanism, and also the increasing reports in which the simulation results are consistent with experiments in many ways. [ 27 , 99 , 100 ] IDPs’ binding–folding processes were investigated extensively by a coarse-grained SBM, [ 58 , 101 – 103 ] built on the basis of the final binding complex structure located at the bottom of the energy landscape, which reproduced the binding–folding mechanism very well in agreement with experiments. Huang et al . applied a plain coarse-grained SBM, which modulates the strengths of the native contacts, to examine the kinetic advantage of IDPs’ binding. [ 104 ] The thermodynamic free energy landscapes and kinetic rates were analyzed comprehensively from the simulation results. The analysis led to the conclusion that, compared to ordered chains, the flexibility in IDPs endows them with a stronger tendency to form the bound complex from an encounter complex with the partners, thus providing a practical explanation for the “flycasting” mechanism. [ 95 ]
Recently, we developed a two-bead SBM with explicit incorporation of electrostatic interactions to investigate IDP histone chaperone Chz1 binding–folding to histone H2A.ZH2B [ 60 ] (Fig.
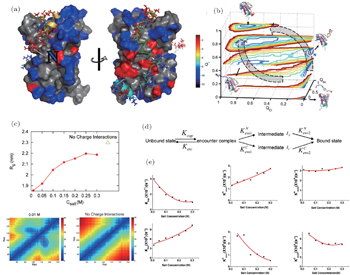 | Fig. 3. Free energy landscape quantifications and kinetic analyses of Chz1 binding–folding to histone H2A.Z-H2B. (a) The charged property of the Chz1- H2A.Z-H2B system. Positively and negatively charged residues are colored by blue and red, respectively. (b) Two parallel binding pathways from free energy landscapes. (c) Collapsed structure in Chz1 at low salt concentrations. The radius of gyration R g and the inter-residue distance describe the degree of collapsed structure at different salt concentrations. (d) Schematic illustration of two parallel binding pathways. (e) Binding rates with different salt concentrations. [ 60 ] |
Although the coarse-grained SBM has made significant progress on the description of IDPs’ binding–folding processes, molecular simulation at the atomic level is in urgent need. However, due to the limit of computational resources, atomistic simulations are often focused on a class of small single-domain proteins on specifically-designed computers. [ 109 , 110 ] To overcome the difficulty, a variety of multi-scale molecular simulations were developed by combining the coarse-grained and atomistic simulations to explore biological processes at a wide range of spatial and temporal scales. We used a multi-scale molecular simulation approach combining coarse-grained SBM and atomistic optimal path calculation method to explore the binding–folding process of IDP inhibitor IA3 to its target enzyme (Fig.
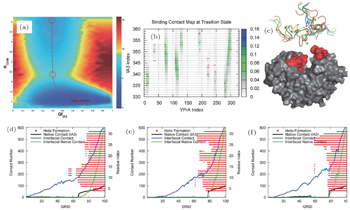 | Fig. 4. Free energy landscape, contact map, and kinetic pathway analyses of IA3 binding–folding to its target enzyme. (a) Free energy landscape projected onto the reaction coordinates of binding ( R com , distance between the center of mass of IA3 and the enzyme) and folding ( Q fIA3 , fraction of the native contacts). (b) Contact map at the transition state ensemble. Colored circles represent contacts formed in the transition states and red points indicate native contacts in the final complex. (c) Starting structures in the atomistic path simulation. (d)–(f) Three typical binding–folding pathways for atomistic simulations. [ 59 ] |
With our recently developed hybrid all-atom model and multi-scale simulation approach, we explored the binding–folding process of an IDP in measles virus nucleoprotein ( α -MoRE) to its target. [ 61 ] α -MoRE, regarded as an IDP, forms a perfect α helix during its molecular recognition. [ 112 – 114 ] Experiments revealed that α -MoRE in solution is not an ideal random coil but in rapid interconversion between the unfolded state and multiple partially helix formed states. [ 115 ] We first set up an REMD simulation with a Charmm22* force field [ 116 ] to explore the inter-chain dynamics of α -MoRE in solution. Through clustering analysis, [ 117 ] we found that α -MoRE dominates at a series of partially helix formed clusters (Fig.
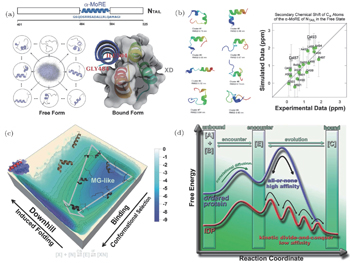 | Fig. 5. Free energy landscape quantifications of α -MoRE binding–folding to its partner. (a) Schematic representations of α -MoRE in solution and binding complex with its partner. (b) Cluster analysis of α -MoRE derived from REMD simulations and chemical shift compared with experiments. The top eight clusters are shown to occupy 70.5% of the population of the trajectory at 298 K. (c) Binding–folding free energy landscape from hybrid SBM. (d) Schematic illustration of kinetic divide-and-conquer binding for IDPs. [ 61 ] |
The quantified multi-dimensional free energy landscapes along various reaction coordinates provide clear pictures on how the binding–folding process in IDPs occurs. Analyses from free energy landscapes, such as interactions and clustering, give comprehensive explanations on the role of nonnative interactions, collapsed structure, downhill folding, intrinsic disorder, and molten globule in IDPs’ biological function. Based on the energy landscape theory, SBM is sufficient to capture the characteristic of IDPs’ binding–folding, indicating that the theory can be applied to proteins with even weakly-funneled or anti-funneled energy landscapes.
Protein realizes its function by binding to its partners. During recognition, protein often undergoes largescale conformational changes to achieve its specific biological function. [ 118 ] Even in isolated states, protein does not always possess a single well-defined structure. Instead, protein often fluctuates among multiple states to facilitate its biological function, implying there are multiple basins on the energy landscapes. [ 48 , 49 , 119 , 120 ] To understand how protein realizes its function, it is essential to understand how functional structural rearrangements occur at the molecular level. Recent developments in experimental techniques, such as single-molecule and nuclear magnetic resonance (NMR) measurements, have improved our knowledge of biomolecular dynamics significantly. However, due to limited spatial and temporal scales, it is still challenging to characterize functional conformational dynamics experimentally. Hence, various molecular simulations have been developed to quantify free energy landscapes.
The basic strategy in simulation is to build a multi-basin SBM potential function. There are three classes of models at different levels: macroscopic model, [ 121 , 122 ] where multiple potentials, each of which has a single energy minimum unambiguously defined by a prior structure, are connected smoothly at the joined point, resulting in a multi-basin energy function; microscopic model, [ 63 – 65 ] where the elementary potential between two atoms in proteins is modeled to have multiple minima, corresponding to multiple structures; mesoscopic model or microscopic mixing contact map, [ 66 , 67 , 123 ] where individual energy terms (usually native contacts) from multiple structures are mixed separately with different mixing protocols.
We first focused on an excellent allosteric model, adenylate kinase (ADK), which is composed of a core domain (CORE), an ATP-binding domain (LID), and a nucleoside monophosphate binding domain (NMP). During its catalytic function, ADK undergoes large-scale domain arrangement from open to closed state. [ 124 , 125 ] To explore the conformational dynamics of ADK, both microscopic and mesoscopic models were investigated in our group. The microscopic model was developed to explore the intrinsic dynamics of ADK. [ 63 ] Using free energy landscapes and contact maps, we addressed the critical dynamical interplay between LID and NMP domain and characterized the hot residues controlling the intrinsic dynamics. Furthermore, the mesoscopic model developed recently with explicit consideration of substrates (AMP and ATP) has made a great contribution to the global understanding of intrinsic and functional dynamics in ADK (Fig.
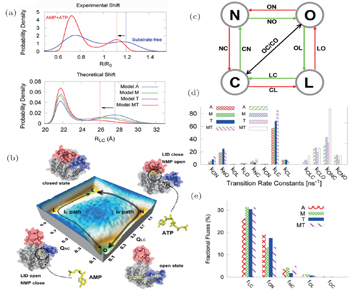 | Fig. 6. Functional free energy landscape and kinetic analyses of ADK with substrates binding. (a) Comparison of the simulation results with the experimental measurements on the LID-CORE distance distributions, which is used to distinguish the open and closed states of ADK. (b) Free energy landscapes of ADK induced by substrates binding. (c) Illustrations of the four-state kinetic model. (d), (e) Kinetic analyses of rates and fluxes during the process of ADK realizing its function with substrates binding. [ 67 ] |
Combining both models, we proposed that only with binding can ADK be induced to a dominate closed state, confirming the pivotal role of substrates on the functional dynamics of ADK. In addition, we found that there are two parallel binding pathways with two intermediates from the quantified energy landscapes. Based on the thermodynamic and kinetic results, we concluded that the motion of the NMP domain is the rate-limiting step for ADK’s conformational change. The remarkable degree of fluctuating intrinsic dynamics in ADK is supposed to favor the functional conformational changes during substrates binding.
Then we explored the functional dynamics of DNA Yfamily polymerase IV (DPO4) binding to its target DNA. [ 68 ] Structural analysis reveals that DPO4 exhibits distinct conformations in the apo and DNA bound state, implying that DPO4 undergoes a large-scale conformational transition during its binding to DNA. [ 126 ] Accordingly, we built a two-basin mesoscopic SBM, aiming to capture the details of flexible protein- DNA recognition. From thermodynamic free energy landscapes, we found that the DPO4-DNA recognition process undergoes four different kinetically connected stages: unbinding state (US), encounter complex (EC), intermediate state (IS), and binding state (BS) (Fig.
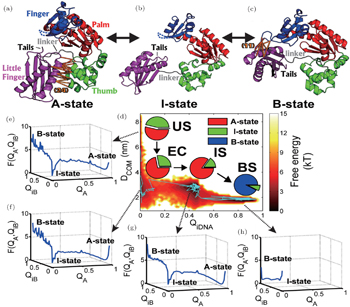 | Fig. 7. Functional free energy landscape of DPO4 binding to its target DNA. Structural illustrations of DPO4 in (a) apo-state, (b) intermediate state, and (c) DNA-bound state. (d) Free energy landscape of DPO4 binding to DNA, with pie-charts representing the population distributions of DPO4 in the three states at each binding stage. (e)–(g) Free energy landscapes of DPO4 in US, EC, IS, and BS binding stages. [ 68 ] |
Built on the energy landscape theory, the multi-basin SBM can explore the functional conformational dynamics in protein during its binding. The multi-basin model aims to capture the intrinsic conformational fluctuation in protein and its role in protein’s function. With the quantified free energy landscapes and kinetic rate/flux analysis, we can gain a global picture of the functional conformational dynamics, giving a deeper understanding of the protein dynamics.
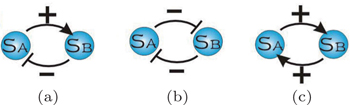
Specificity refers to the discrimination of the same ligand binding to its partner against other possible receptors (Fig.
To circumvent the challenge, an alternative way to determine quantitatively the ligand–receptor binding specificity was proposed. [ 26 , 28 , 36 ] In a thought experiment, one can assume that the N and C terminus of each protein receptor of the protein universe are connected by linkers. In this sense, multiple individual receptors connected by the linkers are equal to a single large composite receptor. The conventional specificity discriminating a ligand binding to a specific receptor against other receptors (Fig.
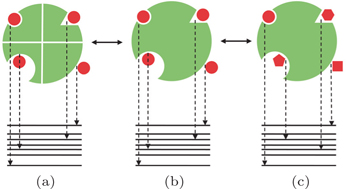 | Fig. 8. Schematic view illustrating the specificity. (a) Conventional specificity: the same ligand (red) binding to diverse receptors (green) with the corresponding energy spectrum. (b) Intrinsic specificity: a particular ligand binding to diverse binding states (modes) of its receptor. (c) Conventional specificity: the same receptor with diverse ligands. [ 36 ] |
The process of receptor–ligand binding can be described and physically quantified by the funnel-like energy landscape, with the native binding mode at the bottom and the binding roughness located in the binding paths. [ 25 – 29 ] From the funnel-like energy landscape, the native conformation has the lowest binding energy (Figs.
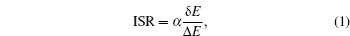

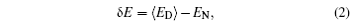

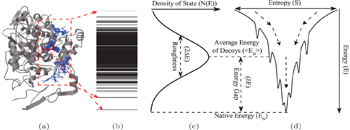 | Fig. 9. Funneled energy landscape and energy spectrum of ligand binding. (a) Diverse docking conformations of the target COX-2 with a drug SC-558, the native binding pose (sticks in red); other decoys (lines in blue). (b) The energy spectrum for decoy ensemble. (c) The resultant binding energy distribution, where Δ E is the variance of energy, 〈 E D 〉 is the average of energy of decoy ensemble, and δ E is the energy gap. (d) Binding energy landscape with a funnel shape pointing to the native state. [ 36 ] |
It is known that specificity and affinity are both required for efficient and specific biomolecular recognition. However, most quantitative descriptions of biomolecular recognition were focused on improving the computation of affinity while lacking the quantification of specificity. Based on the intrinsic specificity and the corresponding intrinsic specificity ratio (ISR), [ 28 ] Liu et al . explored and characterized the binding modes of levamlodipine and human serum albumin (HAS), validating a high ISR value for the binding site of levamlodipine. [ 132 ] Furthermore, Wang et al . developed twodimensional computational drug screening considering both affinity and intrinsic specificity as the selection criteria. [ 28 ] By using the two-dimensional virtual screening with ISR and affinity, Wang et al . successfully identified three active hits against Ras protein. [ 133 – 137 ] Yang et al . further studied the target Ache using two-dimensional virtual screening for potential inhibitors. [ 70 ] Combined ligand screening of the shape and electrostatic similarity as well as local binding site similarity was also applied to search for known drugs against cognitive deficits. For the first time, we found that pazopanib, known as a tyrosine kinase inhibitor for cancer treatment, can inhibit acetylcholinesterase (AchE) activities at the sub-micromolar concentration.
To improve the accuracy of binding affinity prediction, Yan et al . developed the novel scoring functions of protein–ligand, protein–protein and protein–nucleic acid interactions, named SPA, [ 36 ] SPA-PP, [ 37 ] and SPA-PN, [ 38 ] respectively. The optimization strategy is to maximize the performances on intrinsic specificity and affinity predictions simultaneously by tuning the energy parameters according to the funnel-like energy landscape. In addition, Zheng et al . performed twodimensional virtual screening with ISR and affinity evaluated by the scoring function SPA [ 36 ] against flexible Ras protein and protein–protein interactions involving the Ras protein. [ 138 ]
In the equilibrium condition, the binding free energy in vitro can be computed by the kinetic rate constants according to the equation quantifying the relation between the kinetic constants and the thermodynamic features in vitro . However, the condition in vivo is usually a nonequilibrium condition. Consequently, the effectiveness of ligand binding may be affected not only by the thermodynamic properties, but also by the dissociation rate (off-rate constant) determining the residence time (half life). [ 139 , 140 ] The longer the residence time is, the more potent the drug is on the the receptor in vivo . Therefore, not only the thermodynamic affinity and specificity, but also the residence time of the drug on the receptor quantified as the kinetic specificity, determine the duration and effectiveness of the drug.
To calculate the residence time practically, a diffusion process on the energy landscape was used to model the ligand–receptor binding/unbinding kinetics. [ 141 ] In this way, the residence time can be obtained approximately from the kinetic time via the diffusion dynamics. The driving force of this process is determined by the gradient of the free energy landscape. By projecting the free energy onto a reaction coordinate or order parameter, the binding/unbinding kinetics on the energy landscape can be modeled by the following one-dimensional diffusion equation: [ 142 , 143 ]
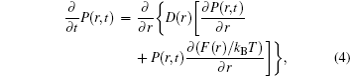
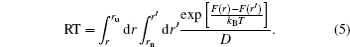
The kinetic specificity quantified by the calculated residence time showed moderate correlations with both thermodynamic stability and specificity, [ 141 ] indicating the thermodynamics and kinetics of ligand binding can be optimized simultaneously. Practically, the intrinsic specificity ratio ISR is less difficult to obtain computationally than experimentally. In contrast, the kinetic specificity is less difficult to obtain experimentally than computationally. The microscopic molecular modeling (molecular dynamics or Monte Carlo simulations) demands tremendous computational time. The coarsegrained diffusion approach here is relatively fast and provides qualitative/semi-quantitative results, although not as accurate as MD or Monte Carlo simulations. The connection of thermodynamics and kinetics bridges a gap in the understanding of drug efficacy. It is also helpful for drug discovery and design. In drug screening, both experimentally and computationally, efforts to identify new lead compounds often concentrated merely on the optimization of the affinity. [ 144 ] Such a strategy neglected the importance of kinetic and thermodynamic specificities. Based on the previous studies on two-dimensional virtual screenings relying on thermodynamic specificity and binding affinity against the Ras protein and Ache protein, Wang et al. have further developed three-dimensional virtual screening taking into account the residence time describing the kinetic specificity. In the drug–target binding system, what determines the residence time of a drug residing in its target is the gap of binding affinity between the native state and the transition state. [ 139 , 140 , 145 – 148 ] Therefore, improving the stability of the native state could decrease the drug potency in vivo , if the affinity change of the transition state is larger than that of the native state. Also, improvement of the affinity may decrease the thermodynamic specificity, if the affinity gap between the native and non-native modes is reduced. This demonstrates the importance of taking the thermodynamic specificity and kinetic specificity as additional criteria for drug discovery.
Based on the energy landscape theory, ISR as quantified thermodynamic specificity and the residence time as quantified kinetic specificity were both quantified computationally. [ 141 ] This gives a quantitative means to choose and optimize the lead compounds computationally with multi-dimensional drug screening strategy by considering both affinity and specificities. Yan et al . [ 69 ] has tested this strategy on the drug targets COXs. As seen in Fig.
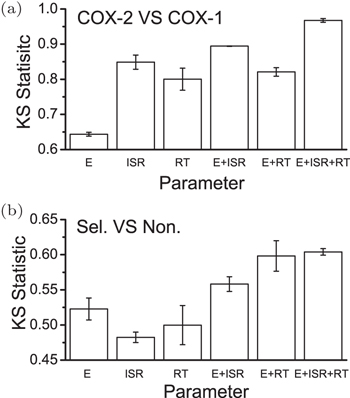 | Fig. 10. Two- and three-dimensional drug and target screening. (a) Target screening: the KS statistic for the discrimination of the COX-2 against COX-1 when complexing with the selective drugs for COX-2. (b) Drug screening: the KS statistic of discrimination of the selective drugs against non-selective drugs when complexing with COX-2. [ 141 ] |
In general, biological systems are nonequilibrium dynamical systems with complex behaviors and varied functions. [ 9 , 10 , 13 , 15 , 40 – 43 , 72 – 78 ] The deterministic dynamics of a generic class of nonequilibrium biological networks can be mathematically modeled by a set of ordinary differential equations, which can be written in the compact form
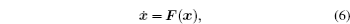
In reality, biological environments are noisy and full of intrinsic and external fluctuations. Taking into account the effects of fluctuations, the Langevin equation usually gives a reasonable description of the system’s stochastic dynamics [ 40 – 43 ]
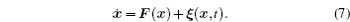
Corresponding to the stochastic dynamics described by the Langevin equation which traces a stochastic trajectory, the probability distribution evolves according to the Fokker–Planck equation (or diffusion equation), which in Ito’s prescription reads [ 40 – 43 ]
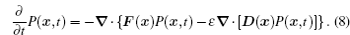
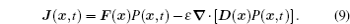
Applying Eq. (
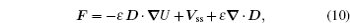
In the small fluctuation regime, the stochastic dynamics of the system can be investigated using the WKB method. The Fokker–Planck equation is expanded in terms of the fluctuation strength parameter ɛ . The zero-fluctuation limit results in the following Hamilton–Jacobian equation: [ 22 , 23 , 41 , 83 , 150 ]
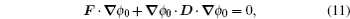
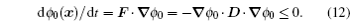
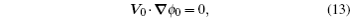
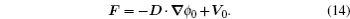
Based on the potential–flux dynamical decomposition, we investigated and extended the fluctuation–dissipation theorem, nonequilibrium thermodynamics, and gauge field formulation. [ 15 , 83 ] When generalized to the nonequilibrium regime, [ 15 , 151 – 154 ] the fluctuation–dissipation theorem for an observable Ω and perturbation on component i of the driving force reads [ 15 ]
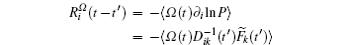
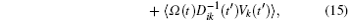
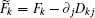
To make contact with the nonequilibrium thermodynamics, we choose the observable Ω = V i and take the equal time limit t = t ′ in Eq. (
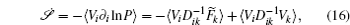
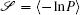
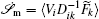
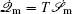
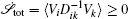
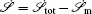
Further, taking the observable as the relative flux velocity 
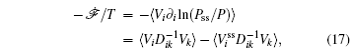

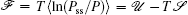
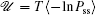
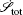

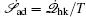
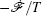
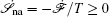
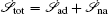
Moreover, a more general set of nonequilibrium thermodynamic equations, taking into account time-dependent external conditions, can be constructed directly from the potential–flux dynamical decomposition, which includes the above two equations as special cases [ 83 ]
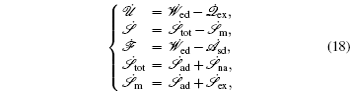
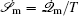
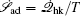
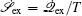
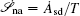
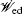
The connection to the gauge field theory [ 15 ] is realized by the covariant derivative 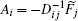
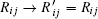
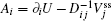

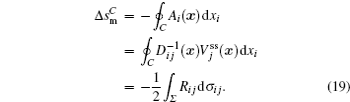
A further connection can be made with Ω = x j in Eq. (
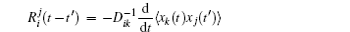
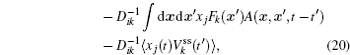
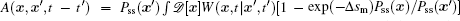
The process of the cell cycle takes place in cell replication and division. It is important for cell growth, cell development, cell proliferation, and cell death. Studying the nature of the cell cycle process is important for exploring the cell functions. The cell cycle has some certain phases, the G1 phase, S phase, G2 phase, M phase, and some check points regulating the process of the cell cycle. It was shown that cell cycle gene regulatory networks control the process of a cell cycle. [ 10 , 11 , 20 , 21 , 159 , 160 ]
The cell cycle gene regulatory networks have been proposed already. [ 20 , 21 , 159 ] We explored the dynamics of the cell cycle in the landscape and flux theoretical framework, [ 10 , 11 , 160 ] using the cell cycle gene regulatory network proposed by Goldbeter. [ 11 , 20 , 21 ] The state of the cell cycle gene regulatory network was characterized by a vector with 44 components. The deterministic dynamics of the network was modeled by a set of nonlinear ordinary differential equations. [ 11 ]
Due to the existence of extrinsic fluctuations and intrinsic fluctuations, the dynamics of the cell cycle network is stochastic and governed by the Langevin and Fokker–Planck equation. To decrease the high dimensionality that stands as an obstacle for solving the Fokker–Planck equation practically, we applied the self-consistent mean field approximation. [ 10 , 11 , 18 ] Then we got the probability of the steady state P ss and the corresponding potential landscape U = –ln P ss .
We projected the landscape and flux, as shown in Fig.
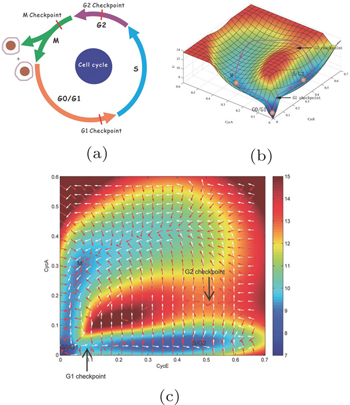 | Fig. 11. (a) The phases with checkpoints for the cell cycle system: the G1 phase, S phase, G2 phase, M phase. (b) G1 phase, S/G2 phase, M phase, G1 checkpoint, and S/G2 checkpoint on the potential landscape. (c) The two-dimensional landscape (the non-zero curl flux is shown in white arrows; the negative gradient of the landscape is shown in red arrows). The diffusion parameter is set as D = 0.05. [ 11 ] |
The driving force is composed of the flux and the landscape in this nonequilibrium cell cycle dynamical system. The curl flux force (flux velocity) is an essential component of the nonequilibrium driving force for the cell cycle, which characterizes the nonequilibrium nature of the cell cycle network. [ 9 – 11 , 13 – 15 , 23 ] It is a rotating vector maintaining the cell cycle oscillation. The input of energy is supplied by the cell nutrition in the cell cycle. The potential landscape quantifies the global robustness and stability for the nonequilibrium cell cycle system. [ 9 – 11 , 13 – 15 , 23 , 149 , 160 ]
We can see from Fig.
We also investigated the global sensitivity analysis and the function of this system. The barrier and the flux reflecting genes and regulatory connections in the cell cycle network can determine the cell cycle function. We show in Fig.
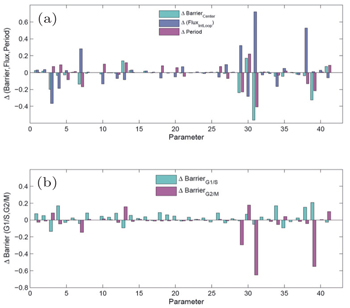 | Fig. 12. Global sensitivity analysis. The barrier (Barrier Center is for global stability, Barrier G1/S is for the G1 checkpoint, Barrier G2/M is for the checkpoint of S/G2), flux and period change as the parameters vary. The horizontal coordinates display 41 parameters. Each parameter is changed 10%. [ 11 ] |
Using the method of global sensitivity analysis, we have identified important regulations and genes affecting the cell cycle function. On the experimental aspect, a few key genes and regulations of the cell cycle have been discovered and verified. The genes and regulations we identified as being important from global sensitivity analysis are consistent with the results from experiments. The pRB activation can decrease the effect of the curl flux and increase the barrier height Barrier G2/M . It can also make the process of the cell cycle longer. [ 11 ]
The cancer cell cycle is an uncontrollable cycling. Its period is much shorter than that of the normal cell. The two components of the driving force, the barrier force and the flux force, are not balanced in the cancer cell cycle. The impact of curl flux overcomes the landscape barrier on the oscillation path. Therefore, decreasing the flux or increasing the barriers may restore the balance between the landscape barrier and curl flux so that the cancer cells can return to the normal state. This process may be realized by varying the genes, the nutrition supply or regulatory connections. We can apply the global sensitivity analysis to identify these variations of gene or environment.
The potential landscape and curl flux theory has also been applied to investigate the mammalian cell cycle. [ 10 , 11 , 160 ] The barrier height on the landscape is a measurement of the global cell cycle robustness and stability. There is a periodic oscillation with four phases and three checkpoints on the cycle path. The gradient of landscape guides the cell cycle system to settle on the cell cycle oscillation. Along the limit cycle, the system is driven by the curl flux. Both landscape and flux direct the cell cycle. Investigation on the mechanism of checkpoints has also been conducted in the context of the landscape and flux framework. [ 9 – 11 ] Global sensitivity analysis of the cell cycle has identified important genes and regulations that determine the global cell cycle function. [ 9 – 11 ] Some of our results have been confirmed in experiments, and some findings can be used to predict potential anticancer strategies.
In the 1940s, Waddington proposed a famous emblem of the epigenetic landscape in the cell development and differentiation. [ 161 ] The growing cell is analogous to a ball rolling from the top of the landscape to the bottom inWaddington’s image. When the ball encounters a bifurcation of the landscape every time, it will choose one of the alternative trajectories eventually. This process was considered as a metaphor of cell differentiation. However, the picture only provides a qualitative understanding of the developmental process of cells. Recently, considerable theoretical effort has been devoted to the cell fate problem. [ 14 , 16 , 18 , 162 – 168 ]
To analyze the process of cell development and differentiation quantitatively, we have utilized the landscape and flux framework. Waddington’s landscape picture can be quantified through investigating an important example of the cell development network consisting of a pair of self-activating and interactively repressing genes. The gene regulatory network governing a binary cell fate decision model has been found in the multipotent stem cells of various tissues. The cell fate determining model masters transcription factors, gene X 1 and gene X 2 . The relative expression levels x 1 and x 2 of genes X 1 and X 2 characterize the state of the network. The dynamics of the model is represented by a set of ordinary differential equations. [ 14 , 165 ] For stochastic dynamics with fluctuations, we can obtain the steady-state probability distribution and derive the potential landscape U = –ln P ss . The developmental/reprogramming paths are quantified by the dominant paths using the path integral method.
In Fig.
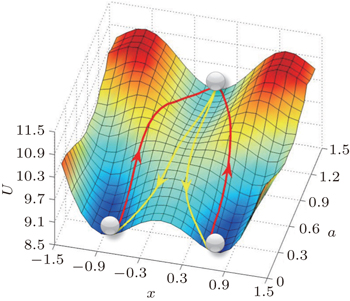 | Fig. 13. The quantified Waddington developmental landscape and pathways. [ 14 ] |
In addition, we have also studied the human embryonic stem cell network, which is composed of nine nodes after integrating previous known networks. [ 169 , 170 ] The dynamics of this network is represented as ordinary differential equations with stochastic forces when fluctuations are taken into account. Within these nine nodes, NANOG is a primary stem cell marker and its higher expression level indicates more stemness. GATA6 and CDX2 are considered as two differentiation markers. Higher GATA6 or CDX2 expression levels indicate higher differentiation. Different combinations of gene expression levels give rise to the stem cell state (attractor), differentiation state, or intermediate states. This human embryonic stem cell network can also be studied quantitatively in the landscape and flux framework. [ 166 ]
The biological pathways of stem cell differentiation/ development and reprogramming can be studied using the path integral approach. The path integral method has found wide applications in different areas of physics and chemistry since it was proposed. It has now been developed and applied to biological systems. Generally speaking, the dynamics of a spatially homogeneous biological system is represented by a set of ordinary differential equations with stochastic forces accounting for fluctuations. An insightful approach to study stochastic dynamical systems is to consider the transition probability from the initial state
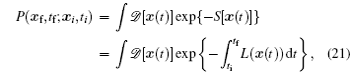
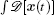
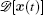
The term ∫ d
As is known, the equilibrium transition state or Kramers rate is an important concept in equilibrium systems. [ 173 ] The forward and backward dominant paths have identical configurations and go through the saddle point of the equilibrium landscape. The equilibrium transition rate from one basin to another for one-dimensional systems with constant diffusion is given by 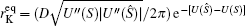
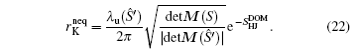
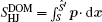
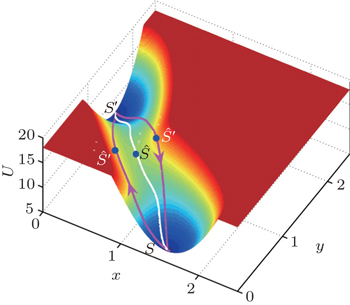 | Fig. 14. The three-dimensional nonequilibrium landscape including the gradient path (white line) and the irreversible dominant transition pathways between the basins S and S′ (purple lines). Here, Ŝ denotes the saddle point and Ŝ′ denotes “the global maximum along the dominant path”. [ 167 ] |
Both the landscape and flux guide the processes of stem cell differentiation. [ 14 , 16 , 18 , 19 ] The probability curl flux is a curling force which breaks detailed balance, leading to the nonequilibrium state of the system. The flux force also drives the biological dominant paths of stem cell differentiation to deviate from the path of steepest descent. Furthermore, due to the flux’s curl nature, the forward and backward dominant paths of the stem cell differentiation and reprogramming process are irreversible. They have different configurations and usually do not pass the saddle point. Therefore, the curl flux breaks time reversal symmetry and provides the direction of time. The flux can even be the major driving force for differentiation and reprogramming of the stem cell as the potential landscape is relatively flat. Thus “flux-directed” process can occur in cell development. The arrow of time in cell development cannot be imposed by the potential landscape alone. [ 12 , 14 , 19 ] It is the curl flux that indicates the arrow of time in cell development. This suggests a resolution of a long standing puzzle of the direction of time in cell development.
Conventionally, cancer has been considered as a disease arising from mutation. The landscape and flux theory provides a different perspective on this issue and forms a quantitative foundation for viewing cancer as a diseased state and associated state transformations. [ 176 ] The hallmarks of cancer [ 176 – 178 ] have been proposed by Weinberg; these hallmarks can be characterized by key genes of cancer. Cancer states originate from the interactions among genes in a cancer gene regulatory network. These networks are general nonequilibrium dynamical systems. We can study these systems using the potential landscape and flux theory. [ 39 ] Our investigation shows that cancer can be viewed as a specific state related to the gene regulatory network. There have also been other studies supporting the view that cancer is a disease associated with a network rather than a disease due to a single mutation. [ 77 , 168 , 179 – 183 ]
We investigated the cancer mechanisms and dynamics by the gene network. [ 39 ] We focused on the cancer marker genes P53, RB, P21, and PTEN. After a literature search, we constructed a cancer gene regulatory network with 32 gene nodes and 111 regulation edges (shown in Fig.
Ordinary differential equations can be used to describe the deterministic cancer gene dynamics. The activation and repression interactions among these genes are modeled by Hill functions, which specify the 32 ODEs for this network. We have also considered the stochastic dynamics of this cancer network with fluctuations. [ 9 , 10 , 14 ] The distribution of the steady-state probability and the corresponding landscape of the cancer regulatory network can be obtained by the method of the self-consistent mean field approximation.
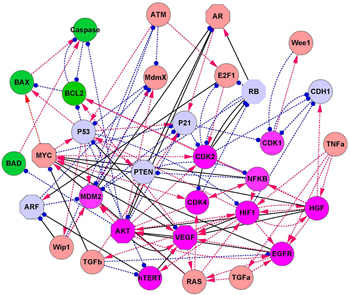 | Fig. 15. The diagram of the cancer network which has 32 nodes and 111 edges. Red arrows denote activation while blue end points represent repression. Green nodes represent apoptosis marker genes; magenta nodes represent cancer marker genes; and light blue represent nodes tumor repressor marker genes. The brown nodes represent other genes. The solid black lines denote the key links, while the octagon nodes denote key genes found by the method of global sensitivity analysis. [ 39 ] |
We reduced the 32-dimensional landscape to a 2- dimensional plane for clarity of presentation. The threedimensional and two-dimensional landscapes are shown in Fig.
We explored the dominant pathways connecting the cancer cell state, apoptosis cell state, and the normal cell state using the path integral method. [ 13 , 14 , 18 , 39 ] The dominant kinetic pathway from the normal state to the cancer state is shown by the yellow path; the magenta path denotes the dominant kinetic pathway from the cancer state to the normal state in Fig.
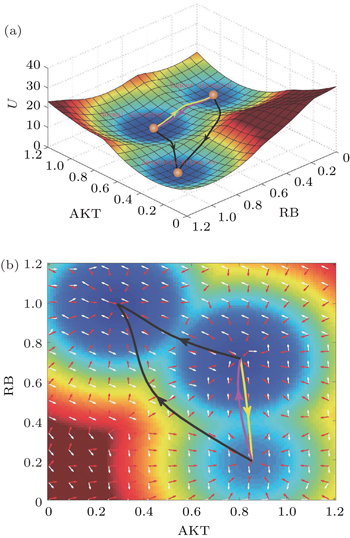 | Fig. 16. The potential landscape for the cancer network. The parameters are evaluated at: degradation constant k = 1, activation strength a = 0.5, repression strength b = 0.5, and diffusion constant D = 0.01. (a) The potential landscape and the kinetic dominant pathways. (b) Two-dimensional landscape of the cancer network. [ 39 ] |
Furthermore, we reduced the system to 21 marker genes from the original 32 marker genes and used a binary code to represent the qualitative characteristic of gene expression levels (high or low). The states and paths of the network can be visualized using the simplified binary gene expression levels (2 21 combinations in totality). [ 39 ] Figure
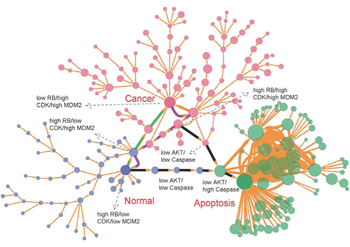 | Fig. 17. The discrete landscape for the cancer network with parameter a = 0.5, b = 0.5, k = 1. Each node represents a specific cell state characterized by the qualitative expression levels of the corresponding marker genes. The nodes of blue, red, and green represent, respectively, the cell states evolving into the normal, cancer, and apoptosis states. The apoptosis pathways are represented by the black paths. The green and magenta paths denote, respectively, the pathways from the normal state to the cancer state and from the cancer state to the normal state. [ 39 ] |
Fisher’s fundamental theorem of natural selection [ 185 ] and Wright’s fitness landscape [ 184 ] are widely used to interpret the evolutionary adaptation as the mean fitness maximization. [ 75 – 77 ] However, the evolutionary dynamics of non-equilibrium biological systems is complex and may no longer follow maximization of the mean fitness. The coevolving systems may enter an endless cycle rather than reaching the mean fitness maximum. We studied the general evolutionary dynamics with the potential and flux landscape theory. We found that the conventional Fisher’s fundamental theorem of natural selection and Wright’s fitness landscape are based on equilibrium systems. Hence, they cannot explain many phenomena related to the nonequilibrium nature of systems. A typical example is Van Valen’s Red Queen hypothesis, which indicates that an ecosystem can enter endless evolution processes even if the physical environment remains unchanged. [ 23 ]
The mathematical framework of evolutionary theory is based on the description of the change in allele frequencies x i . If the fitness w i j is not dependent on the allele frequencies, the mean fitness is a Lyapunov function as indicated in Fisher’s fundamental theorem of natural selection: d w̄ /d t = V A ( w )/ w̄ ≥ 0 (where the additive genetic variance 
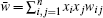
For general evolutionary dynamics, the system enters the nonequilibrium regime and the mean fitness does not always increase. The conventional evolutionary theory based on mean fitness then breaks down. [ 23 ] Some researchers believe that no general potential function exists whose optima are searched for in the evolution dynamics. [ 186 ] One may ask if there is a general potential function for evolution and if so what it is. The solution can be obtained from the potential–flux landscape theory. As a Lyapunov function, the intrinsic potential ϕ 0 can be used to redefine the adaptation for general evolutionary dynamics. [ 23 ]
By including selection and genetic drift, the nonequilibrium intrinsic potential ϕ 0 satisfies the Hamilton–Jacobi equation as given in Eq. (
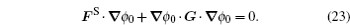
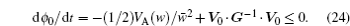
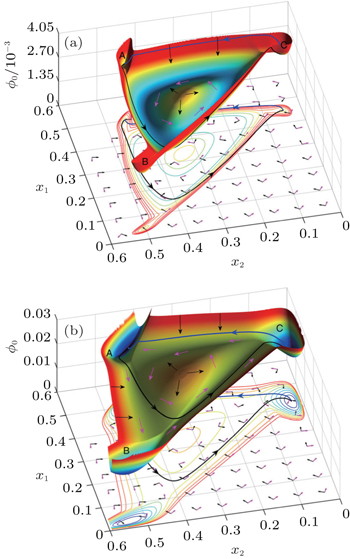 | Fig. 18. Landscapes of different phases (with parameters (a) β = 0.11, (b) β = 0.17). The arrows are schematic, showing the two components of the driving force: the gradient of potential − |
An evolutionary system reaches its optima when d ϕ 0 /d t = 0. In the frequency-independent selection case, the system is in detailed balance with
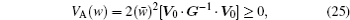
What is the cause of the non-zero intrinsic flux velocity? If there is no biotic interaction, the natural selection comes from the external physical environment, as frequency independent selection would be a gradient force given by Wright’s fitness landscape. Biotic interactions can sustain a genetic variation in fitness and thus give rise to endless evolution. The effect caused by biotic interactions was indicated by Van Valen in the Red Queen hypothesis. [ 187 ] According to this hypothesis, endless evolution can be sustained by biotic interactions even if the physical environment remains unchanged, that is, biotic interaction can lead to endless evolution.
In the potential–flux landscape framework, we can clearly see the origin of the Red Queen phenomena. The endless evolution comes from the non-zero flux of biotic interactions even when the evolution potential has reached its optima. Therefore, Van Valen’s Red Queen hypothesis is the biological expression of the intrinsic flux: the system lies in the optimum where the gradient of potential is zero, while the intrinsic flux drives the endless evolution. As Van Valen himself remarked, this cannot be explained by the traditional evolutionary theory, since the flux is the missing part in the traditional evolutionary theory. [ 23 ]
Ecological systems interact with each other through cooperation and competition. [ 188 ] Exploring the stability of ecological systems is essential for understanding the mechanisms governing the dynamics of species and populations. [ 188 ] Ecological systems involve numerous interactions among the species which are generally non-linear complex dynamics. Much effort has been devoted to studying the stability of ecological systems. [ 189 – 192 ] Most of them focused on the analysis of local linear stability. It is thus important to study the global stability of ecological systems.
Previously, researchers have concentrated on deterministic models. In reality, both extrinsic and intrinsic fluctuations may exist in ecological systems, which can affect the global behaviors of ecological systems. The intrinsic fluctuations generally arise from the finite size of the ecological systems, while the extrinsic fluctuations typically come from the environment. The analysis of global stability is important for investigating the robustness of ecological systems under the influence of extrinsic and intrinsic fluctuations. [ 191 , 192 ]
Nonlinear ordinary differential equations can be used as a mathematical model of the deterministic dynamics of ecological systems with the interactions of predation, competition, and mutualism. [ 189 , 190 ] There are two basic types of relationships between species in ecological systems: a positive beneficial interaction (activation) and a negative compromising interaction (repression) as shown in Fig.
 | Fig. 19. (a) Relationship of predation. (b) Relationship of competition. (c) Relationship of mutualism. [ 22 ] |
The landscape and flux theory has been applied to investigate the ecological systems with predation, competition, and mutualism for two species. We also added some restrictions and modifications on these ecological models so that they may be more realistic. [ 22 , 188 , 193 ] We acquired the steady-state probability distribution P ss of ecological models with stochastic fluctuations as in real ecological systems. Then the potential landscape is obtained from the relation: U = −ln P ss . It can be applied to investigate the global robustness and stability of ecological systems.
In the past studies, it was essential to address the global stability of the system using Lyapunov functions. In 1931, Volterra proposed an analytical Lyapunov function for a specific model of predation. [ 190 ] Then the analytical Lyapunov function [ 191 , 192 ] was explored in many ecological systems. For some simple ecological models, Lyapunov functions were obtained. However, there were no general methods to find the Lyapunov function of more realistic ecological systems. A more systematic approach has emerged to fill the gap of identifying the Lyapunov function of general ecological systems. [ 22 ] Hence, we can now use the Lyapunov function to investigate the global robustness of a wider range of ecological systems. [ 22 ]
Figure
In the predation model, the potential landscape U with a Mexican hat shape for small fluctuations (characterized by a small diffusion coefficient) is shown in Fig.
The population potential landscape U and intrinsic potential landscape ϕ 0 for the competition model with the parameters evaluated at a 1 = a 2 = 0.1, L 1 = L 2 = 0.3, α = 1.0, D = 0.01 are shown in Figs.
The population potential landscape U and intrinsic potential landscape ϕ 0 for the mutualism model are shown in Figs.
In the above, we studied three crucial ecological modes: predation, competition, and mutualism. We can see the ecological system may have multiple basins of attraction and also a limit cycle which has a landscape of the Mexican hat shape. We demonstrated the two key components determining the nonequilibrium dynamics of these ecological systems: the non-zero curl flux and the negative gradient of the landscape. [ 22 ]
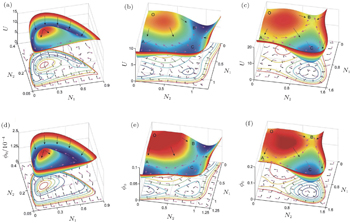 | Fig. 20. (a)–(c) The population potential landscape U ((a) model of predation; (b) model of competition; (c) model of mutualism). (d)–(f) The intrinsic potential landscape ϕ 0 ((d) model of predation; (e) model of competition; (f) model of mutualism). On the top row, the flux velocity and the negative gradient of the population potential are denoted, respectively, by the purple arrows and black arrows. On the bottom row, the intrinsic flux velocity and the negative gradient of the intrinsic potential landscape are denoted, respectively, by the purple arrows and black arrows. [ 22 ] |
We have also applied our theory to quantify the robustness of ecological systems through changing parameters that control the underlying landscape topography. We can investigate a variety of parameters to search for systems with higher stability quantified by the barrier heights of the underlying landscape topography. Thus the stability and decision making strategy for ecological systems can be achieved by modulating the control parameters. The global sensitivity analysis can be applied to investigate the effects of different values of parameters on the stability and robustness of ecological systems. We can also identify the species and interactions that are important for determining the global robustness of the ecological system by studying the topography of the potential landscape. The method we proposed for investigating the global robustness and stability can be used to explore more realistic ecological systems. [ 22 ]
Understanding the functions of the human brain is always a grand goal of neuroscience. As a complex dynamical system, the brain is responsible for various vital functions. [ 194 – 199 ] Although individual neurons have all sorts of behaviors, complicated physiological and cognitive functions in the brain are implemented by the neural circuits consisting of a large number of neurons rather than individual neurons. The cognitive functions such as decision-making, sensory, learning, and memory are related to special complex patterns of activities generated by neural circuits. [ 200 – 202 ] Despite the significant efforts in both theoretical and experimental approaches, global and quantitative understanding of the nature of large neural networks is still challenging.
Many models have been suggested for exploring the behaviors of neural circuits and corresponding biological functions. [ 195 , 197 – 199 ] The behavior of a single neuron can be quantitatively described by the Hodgkin–Huxley model based on its biological features. [ 197 ] Hopfield developed a model [ 198 , 199 ] to uncover the global characteristics of large neural circuits. Assuming the neural circuits are symmetrically connected, he constructed an energy landscape that decreases with time. [ 24 , 199 ] The dynamics of the symmetric neural circuit is dominated by the gradient force of the energy function. Then the associative memory function of the symmetric neural networks can be quantitatively described as shown in Fig.
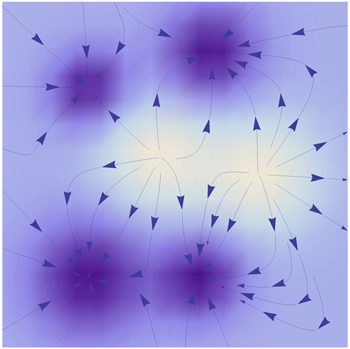 | Fig. 21. The schematic drawing of the energy landscape of a symmetric neural network. [ 24 ] |
The Hopfield model is able to show a good associative memory property. However, this model fails to apply in general neural networks since the connections among neurons are mostly asymmetric rather than symmetric in realistic neural circuits. Besides, there is evidence showing that oscillatory behaviors with different rhythms in neural circuits play crucial roles in cognitive processes. [ 201 , 202 ] Yet in Hopfield’s symmetric neural networks, oscillations can never exist because the driving force here is a pure gradient of the potential. Fortunately, unlike the energy defined by Hopfield, the intrinsic potential ϕ 0 we introduced is always a Lyapunov function regardless of the symmetry or asymmetry of the circuit. [ 24 ] We have shown that the dynamics of neural networks is driven by both the gradient force of the potential and the curl flux force. [ 9 , 10 , 24 ] The flux can provide the main driving force for oscillations. [ 24 ]
We applied our landscape and flux framework to a network consisting of twenty model neurons. [ 24 ] Then we quantified the intrinsic potential ϕ 0 , which is a Lyapunov function of the system, through taking the zero fluctuation limit of the potential landscape U . For the sake of visualizing the multi-dimensional results in the state space, we chose two state variables from the twenty model neurons and integrated the other eighteen variables to map out the landscape. [ 24 ] For the symmetrically connected neural circuit, the intrinsic potential landscape ϕ 0 is shown in Fig.
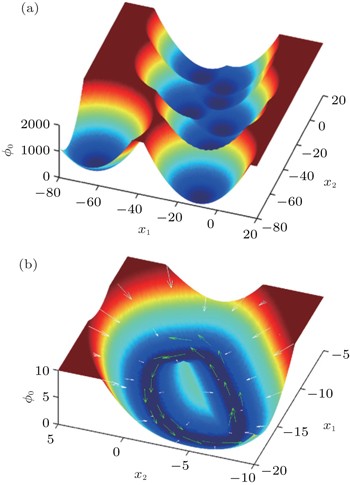 | Fig. 22. (a) The intrinsic potential landscape ϕ 0 of the symmetric neural circuit. (b) The intrinsic potential landscape ϕ 0 and the corresponding driving force: white arrows represent the negative gradient force from the potential landscape and green arrows represent the curl flux force. [ 24 ] |
As discussed, in Hopfield’s symmetric neural network, the dynamics is only driven by the gradient force and there is no flux. Such a symmetric network corresponds to the equilibrium case of neural systems. In reality, the neural networks are open systems which constantly exchange materials and energy with the environment. We found that the nonzero flux in the asymmetric neural circuits are closely associated with the asymmetric part of the driving force. [ 24 ] The flux which breaks the detailed balance of the dynamical system is the signature indicating that the neural network is in a nonequilibrium state. Our results suggest that although the number of point attractors storing memories decreases when the network becomes more asymmetric, continuous attractors, for example, limit cycles, may occur, which are able to store memory in a sequential form. Different memories can be associated by the flux. The flux may provide a quantitative measure to explore the competition between memory associativity and storage capacity. We also found that the flux plays the key role in controlling repetitive physiological activities and biological rhythms because of its close association with the frequency of oscillations. To test this, we applied our nonequilibrium landscape and flux theory to a neural network model which can describe the dynamics of REM sleep cycle. [ 203 , 204 ] Based on the global quantification of the landscape, we made a global sensitivity analysis to investigate the effects of key factors on the stability and function of the system. [ 24 ] Our theoretical results agree well with experimental recordings.
This review has presented a theoretical framework of landscape and flux theory applied to a variety of biological systems. The energy landscape has become a powerful tool to understand biomolecular dynamics. However, it is often difficult to directly measure the energy landscape topography in reality. A novel way to explore the energy landscape is presented by the quantified energy landscape approach through thermodynamic and kinetic measurements. With the quantified energy landscapes, we are able to depict the biomolecular dynamics globally and physically. Based on the energy landscape theory, SBM has made a significant progress on simulating protein folding and binding processes. Even for IDPs, the energy landscapes of which are expected to be weakly funneled or anti-funneled, SBM can make excellent predictions consistent with experiments. With some adjustments, SBM can also be applied to investigate the large-scale conformational dynamics in an enzyme during its realization of function. Accumulating evidence stresses the crucial role of the energy landscape in various biomolecular dynamics, strengthening the importance of the energy landscape theory in modern molecular biology. A variety of simulation approaches based on the energy landscape theory require development and the applications are expected to have wide use in the future.
Biomolecular recognition is fundamental to the biological activities mediated by forming complexes between ligands and receptors. It is thus critical to study biomolecular recognition in order to understand the nature of these biological activities. Besides, such study can also find its direct use in drug discovery and design. Generally, both affinity and specificity are required for biomolecular recognition to realize its function, since affinity determines the stability of the complex and specificity controls the discrimination against competitive binding partners. The specificities of ligand binding can be calculated quantitatively using the energy landscape theory. Therefore, the energy landscape theory offers a practical way to predict and optimize interactions of ligand binding by considering the positive design (affinity) and negative design (specificity). In addition, with the thermodynamic and kinetic specificities quantified, multi-dimensional drug screening and target identification are promising means to avoid the side effects of drugs and seek specific targets.
The landscape and flux theoretical framework quantifies the global nature of the stability and dynamics of nonequilibrium biological systems, facilitating the discovery of physical mechanisms and basic principles behind complex dynamical behaviors of biological processes. The central idea of the framework consists of two essential components: (i) the potential landscape, obtained from the steady-state probability distribution, which gives a global characterization of the system’s stability; (ii) the curl flux, quantified by the steady-state probability flux, which characterizes detailed balance breaking in nonequilibrium biological systems. Both the potential landscape and the curl flux contribute to the nonequilibrium dynamics of biological systems. The potential landscape drags the system downward to the valleys, while the curl flux drives the circulating process. For some, this may be reminiscent of the Chinese Yin–Yang philosophy. The potential landscape (Yin) and the curl flux (Yang), like a complementary pair promoting and constraining each other, are both needed to give a complete characterization of the global stability and dynamics of nonequilibrium biological systems. We have demonstrated the applications of the landscape and flux theory in multiple biological systems across a wide range, including cell cycle, stem cell, cancer, evolution, ecosystems, and neural networks.
It is challenging to understand the complex behaviors of nonequilibrium biological systems. In this review, we have presented our landscape and flux theoretical framework for quantitative global study of biological systems. We have focused on the theoretical aspects of the subjects here. It is worth noting that the theoretical explorations may be limited by our understanding of the topics and more experiments need to be carried out. Only through the combination of theoretical investigations and experimental studies can the field advance. We hope our theoretical framework can further contribute to the understanding of complex nonequilibrium biological processes through extending its applications in both depth and width and by making more contact with experiments.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 | |
| 63 | |
| 64 | |
| 65 | |
| 66 | |
| 67 | |
| 68 | |
| 69 | |
| 70 | |
| 71 | |
| 72 | |
| 73 | |
| 74 | |
| 75 | |
| 76 | |
| 77 | |
| 78 | |
| 79 | |
| 80 | |
| 81 | |
| 82 | |
| 83 | |
| 84 | |
| 85 | |
| 86 | |
| 87 | |
| 88 | |
| 89 | |
| 90 | |
| 91 | |
| 92 | |
| 93 | |
| 94 | |
| 95 | |
| 96 | |
| 97 | |
| 98 | |
| 99 | |
| 100 | |
| 101 | |
| 102 | |
| 103 | |
| 104 | |
| 105 | |
| 106 | |
| 107 | |
| 108 | |
| 109 | |
| 110 | |
| 111 | |
| 112 | |
| 113 | |
| 114 | |
| 115 | |
| 116 | |
| 117 | |
| 118 | |
| 119 | |
| 120 | |
| 121 | |
| 122 | |
| 123 | |
| 124 | |
| 125 | |
| 126 | |
| 127 | |
| 128 | |
| 129 | |
| 130 | |
| 131 | |
| 132 | |
| 133 | |
| 134 | |
| 135 | |
| 136 | |
| 137 | |
| 138 | |
| 139 | |
| 140 | |
| 141 | |
| 142 | |
| 143 | |
| 144 | |
| 145 | |
| 146 | |
| 147 | |
| 148 | |
| 149 | |
| 150 | |
| 151 | |
| 152 | |
| 153 | |
| 154 | |
| 155 | |
| 156 | |
| 157 | |
| 158 | |
| 159 | |
| 160 | |
| 161 | |
| 162 | |
| 163 | |
| 164 | |
| 165 | |
| 166 | |
| 167 | |
| 168 | |
| 169 | |
| 170 | |
| 171 | |
| 172 | |
| 173 | |
| 174 | |
| 175 | |
| 176 | |
| 177 | |
| 178 | |
| 179 | |
| 180 | |
| 181 | |
| 182 | |
| 183 | |
| 184 | |
| 185 | |
| 186 | |
| 187 | |
| 188 | |
| 189 | |
| 190 | |
| 191 | |
| 192 | |
| 193 | |
| 194 | |
| 195 | |
| 196 | |
| 197 | |
| 198 | |
| 199 | |
| 200 | |
| 201 | |
| 202 | |
| 203 | |
| 204 |


