† Corresponding author. E-mail:
Project supported by the Deanship of Scientific Research (DSR) King Abdulaziz University, Jeddah, Saudi Arabia (Grant No. 32-130-36-HiCi).
We investigate the Cattaneo–Christov heat flux model for a two-dimensional laminar boundary layer flow of an incompressible Oldroyd-B fluid over a linearly stretching sheet. Mathematical formulation of the boundary layer problems is given. The nonlinear partial differential equations are converted into the ordinary differential equations using similarity transformations. The dimensionless velocity and temperature profiles are obtained through optimal homotopy analysis method (OHAM). The influences of the physical parameters on the velocity and the temperature are pointed out. The results show that the temperature and the thermal boundary layer thickness are smaller in the Cattaneo–Christov heat flux model than those in the Fourier’s law of heat conduction.
The researchers at present are engaged in exploring the flows of non-Newtonian fluids at various aspects. Non- Newtonian fluids are very popular due to their importance in our daily life. Examples of such fluids include sugar solutions, apple sauce, lubricants, shampoos, cosmetic products, tomato ketchup, and many others. There is no single constitutive relation describing the characteristics of all non-Newtonian fluids. The simplest subclass of the rate-type fluid is the Maxwell fluid. It only predicts the stress relaxation effects but not the stress retardation effects. Owing to such a disadvantage, an Oldroyd-B fluid model was proposed to investigate both stress relaxation and retardation effects. This model was studied in the past by various investigators under different flow geometries and physical aspects. Some studies on flows of an Oldroyd-B fluid can be found in Refs. [ 1 ]–[ 7 ]. Besides these, Shivakumara and Sureshkumar [ 8 ] reported the effects of flow and quadratic drag on the stability of an Oldroyd-B fluid in a porous space. Khan and Zeeshan [ 9 ] addressed the electrically conducting flow of an Oldroyd-B fluid induced by sawtooth pulses. Liu et al . [ 10 ] analyzed the unsteady Couette flow of an Oldroyd-B fluid with fractional derivative. The authors reported the solutions through the Laplace transform method. Swamy and Sidram [ 11 ] discussed the effect of rotation on the thermal convection flow of an Oldroyd-B fluid. The influences of viscoelastic parameters in the thermal convection flow of an Oldroyd-B fluid with constant heat flux were discussed by Niu et al. [ 12 ] Shivakumara et al. [ 13 ] addressed the thermal convection instability of an Oldroyd-B fluid saturating through a porous medium. The steady stagnation point flow of an Oldroyd-B fluid with mixed convection was numerically analyzed by Sajid et al . [ 14 ]
The dynamics of heat transfer phenomenon is a subject of special attention due to its abundant applications in engineering and industrial processes. Examples of such applications include wire drawing, cooper materials, nuclear reactor cooling, heat conduction in tissues, refrigeration, heat pumps, energy production, cooling of electronic devices, etc. The Fourier’s law of heat conduction [ 15 ] explores the characteristics of heat transfer mechanism at various aspects. The main disadvantage of this model is that it leads to a parabolic energy equation which indicates that the initial disturbance is instantly experienced by the medium under observation. To overcome this disadvantage, Cattaneo [ 16 ] presented the modified Fourier’s law of heat conduction by introducing a relaxation time term. The frame-indifferent generalization of Cattaneo’s law through the implementation of Oldroyds’ upper convective derivative was developed by Christov. [ 17 ] Ostoja-Starzewski [ 18 ] gave the mathematical derivation of the Maxwell–Cattaneo equation by involving a material time derivative of heat flux. The stability and uniqueness of the solutions constructed by the Cattaneo–Christov heat flux model were discussed by Tibullo and Zampoli. [ 19 ] The numerical solutions of an incompressible thermal convection fluid with the Cattaneo–Christov model were constructed by Straughan [ 20 ] and Haddad. [ 21 ] The structural stability and uniqueness of the Cattaneo–Christov heat flux equations were reported by Ciarletta and Straughan. [ 22 ] Al-Qahtani and Yilbas [ 23 ] provided the closed form solutions of Cattaneo and stress equations via the Laplace transform method. Papanicolaou et al. [ 24 ] investigated the influence of the thermal relaxation time in the Cattaneo–Maxwell equations subjected to vertical and horizontal temperature gradients. Very recently, Han et al . [ 25 ] considered the Cattaneo–Christov heat flux model for a boundary layer flow of Maxwell fluid over a stretching sheet. The authors developed the homotopic solutions. Mustafa [ 26 ] reported the numerical and homotopic solutions for a two-dimensional flow of Maxwell fluid in a rotating frame. Bissell [ 27 ] discussed an oscillatory convection flow with the Cattaneo–Christov hyperbolic heat model.
In the present analysis, we introduce the Cattaneo– Christov heat flux model for a two-dimensional boundary layer flow of an Oldroyd-B fluid over a stretching sheet. An incompressible laminar fluid is taken into account. The governing nonlinear ordinary differential equations are solved by the optimal homotopy analysis method (OHAM). [ 28 – 33 ] Convergent series solutions are developed. Graphical results of dimensionless velocity and temperature fields are sketched and examined.
We consider a two-dimensional boundary layer flow of an incompressible Oldroyd-B fluid over a linearly stretching sheet. The laws of conservation of mass and momentum for the incompressible fluid are
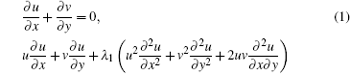
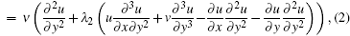

The Cattaneo–Christov heat flux model can be written as [ 17 , 19 ]
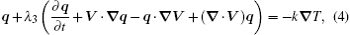
The energy equation for the steady incompressible boundary layer flow is
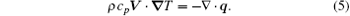
The temperature equation governing the steady-state laminar flow is

The associated boundary conditions for the temperature are
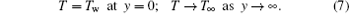
In the above equations, α is the thermal diffusivity, T w is the temperature at the wall, and T ∞ is the ambient fluid temperature.
Equations (

The equations of momentum, energy, and concentration in dimensionless form are

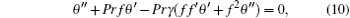

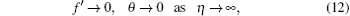
We solve Eqs. (
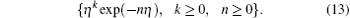
We can express f ( η ) and θ ( η ) in the following forms: [ 35 , 36 ]
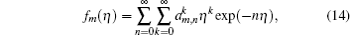
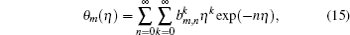
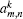

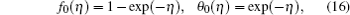
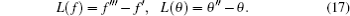
The above initial guess and auxiliary linear operators satisfy the following properties:
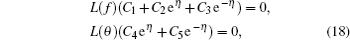
The zero order problems are defined as [ 37 , 38 ]
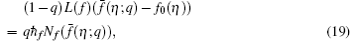
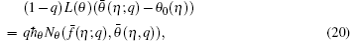
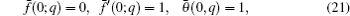
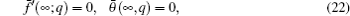
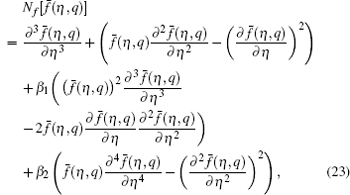
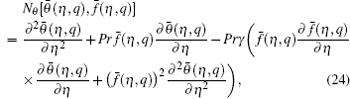

When we increase q from 0 to 1, then f ( η , q ) and θ ( η , q ) vary from f 0 ( η ) and θ 0 ( η ) to f ( η ) and θ ( η ), respectively. By using the Taylor series expansion, we have
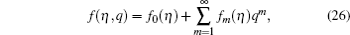


The convergence of the above series highly depends on the suitable values of ℏ f and ℏ θ . Select ℏ f and ℏ θ properly such that equations (
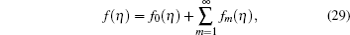

The m -th order problems can be constructed as follows:
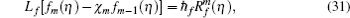
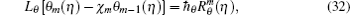
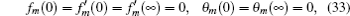
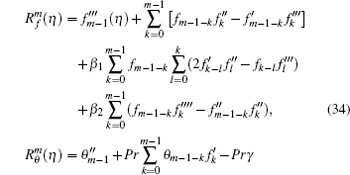
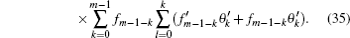
The general solutions can be written as




The squared residuals of the governing equations are defined in the following forms:
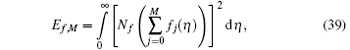
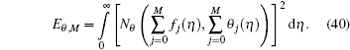
Such a kind of error is considered in various recent papers. [ 29 – 33 ] The best possible values of ℏ at a given order of approximation may be computed by minimizing the squared residuals E f , M and E θ , M . This can be achieved through the command Minimize of the software Mathematica (see Ref. [ 28 ] for details). The optimal values of ℏ for the functions f and θ are given in Tables
| Table 1. Optimal auxiliary parameter ℏ for function f at the 15th order approximation for different β 1 when β 2 = 0.5. . |
| Table 2. Optimal auxiliary parameter ℏ for function θ at 15th order approximation for different γ when β 2 = 0.5. . |
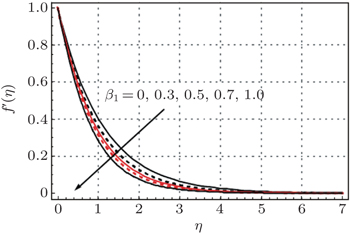
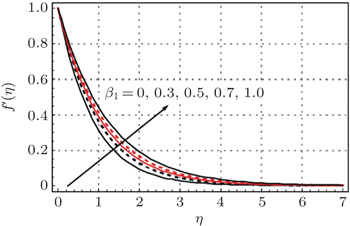
Figures
The variations in dimensionless temperature profile θ ( η ) corresponding to different Deborah numbers β 1 and β 2 , Deborah number γ with respect to the heat flux relaxation time and Prandtl number Pr are shown in Figs.
 | Fig. 3. Variation of dimensionless temperature field θ ( η ) with η for different β 1 when β 2 = 0.2, γ = 0.3, and Pr = 1.4. |
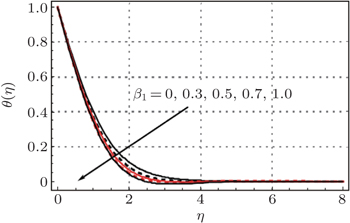 | Fig. 4. Variation of dimensionless temperature field θ ( η ) with η for different β 2 when β 1 = 0.4, γ = 0.3, and Pr = 1.4. |
 | Fig. 5. Variation of dimensionless temperature field θ ( η ) with η for different γ when β 1 = 0.4, β 2 = 0.2, and Pr = 1. |
Tables
 | Fig. 6. Variation of dimensionless temperature field θ ( η ) with η for different Pr when β 1 = 0.4, β 2 = 0.2, and γ = 0.3. |
| Table 3. Comparison with f ″(0) obtained by Abel et al . [ 39 ] and Megahed [ 40 ] for different β 1 when β 2 = 0. . |
| Table 4. Comparison with f ″(0) obtained by Sadghey et al . [ 41 ] and Mukhopadhyay [ 42 ] in the limiting case for different β 1 by fixing β 2 = 0. . |
| Table 5. Values of f ″(0) for different β 2 when β 1 = 0.4. . |
| Table 6. Values of − θ ′(0) for different β 2 , Pr , and γ when β 1 = 0.5. . |
We explore the properties of the Cattaneo–Christov heat flux model for a two-dimensional hydrodynamic boundary layer flow of an Oldroyd-B fluid over a stretching sheet. The obtained key features are listed below.
The velocity field decreases while the temperature profile increases as the Deborah number β 1 increases. The Deborah number β 2 has quite opposite effects on the dimensionless velocity field and the temperature profile. The low temperature profile and thin thermal boundary layer thickness are observed in the case of the Cattaneo–Christov heat flux model in comparison to the simple Fourier’s law of heat conduction. The larger Prandtl number leads to a reduction in the temperature profile and thermal boundary layer thickness.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 |