An inorganic crystalline material is structured by a symmetric, periodic lattice. Because of thermal vibrations, lithium ions may shift off the equilibrium center and hop into an adjacent vacant lattice site or interstitial site. If an electrical gradient field exists across the crystalline lattice, a net diffusion along the electrical direction will result from random hopping, which leads to long-range ionic transport. ^{[ 4 ]} The hopping of ions usually happens along adjacent lattice sites where the lowest energy barrier exists. Because of the symmetric, periodic arrangement of a crystalline structure, the diffusion pathway can be extrapolated from the analysis of ion hopping in a unit cell.

In polycrystalline materials, the symmetric and periodic structures end at the edge of a single crystal. The area connecting two crystals is called a grain boundary, and its elemental composition and structure may be dramatically different from the grain. In terms of symmetry and thickness, grain boundaries can be divided into several types. (i) Grain boundary which has a highly defective and distorted crystal structure, in which the atom coordination decreases but the long periodical structure can still be found. The thickness of such a grain boundary is less than that of a unit cell, or even nearly a single-atom layer. (ii) Grain boundary consisting of atoms that are randomly arranged, without any periodicity. This type of grain boundary is only several atoms thick. (iii) Grain boundary with crystalline periodic atomic arrangement. The thickness is larger than a single unit cell. (iv) Amorphous grain boundary with disordered atomic arrangement. This type of grain boundary is also more than several atoms thick. ^{[ 5 – 8 ]}

The concentration of charge carriers, charge mobility, diffusion pathway, and activation energy are all different at interfaces. In order to further understand the different diffusion properties at grain boundaries, several physical models are introduced. According to the structural properties of polycrystalline substances, Beekmans and Heyne proposed the Brick layer model (as shown in Fig.  1 ), ^{[ 9 , 10 ]} in which the polycrystalline substance is treated as an array of cubic grains, separated by flat grain boundaries. Depending on the difference of electrical properties between the grain and grain boundary, such as resistance, capacitance, and permittivity, ions can either transport across both the grain and grain boundary or only along the grain boundary. The Brick layer model is a macroscopic model, which does not account for the micro transport mechanism at the grain boundary. To gain insight into the micro mechanism of interfacial diffusion, the space charge layer model was proposed (as shown in Fig.  2 ). ^{[ 11 ]} Because of the difference in terms of structure, the electrical potential at grain boundaries is different from that in grains. Based on the thermodynamic equilibrium, the corresponding defect concentration in grains differs from that at grain boundaries, which leads to a difference in concentration of charge carriers. The mobility of ion diffusion is assumed to be the same both within grains and at grain boundaries; therefore, the difference in conductivity can be obtained from the difference in concentration of charge carriers.

Fig. 1.

	Figure Option View Download New Window
	Fig. 1. (a) Brick layer model for polycrystalline ceramic; (b) possible ion diffusion pathways: (i) across grain and grain boundary, (ii) along grain boundary. [ 12 ]

Fig. 2.

	Figure Option View Download New Window
	Fig. 2. (a) Defect concentration profile near the interface based on space charge layer model; (b) model microstructure for a polycrystalline solid. [ 12 ]

In 1973, Liang found that the ionic conductivity of LiI increased upon being prepared as a composite with Al ₂ O ₃ , as shown in Fig.  3 . ^{[ 13 ]} The maximum conductivity was achieved at approximately 1:1 ratio of LiI and Al ₂ O ₃ . ^{[ 14 ]} Because Al ₂ O ₃ is an insulator, the increase of conductivity was ascribed to the high conductivity at the interface. In order to understand the transport property in composite materials with conductor and insulator, a percolation model was proposed, as shown in Fig.  4 . ^{[ 14 , 15 ]} In this type of composite system, two kinds of pathways exist for ionic transport: across the grain and along the interface. Electrical current flows only along the shortest pathway. Depending on the volume ratio and dispersion state of two phases, different transport pathways will form. In addition to the percolation model, Dudney proposed a resistance network model, ^{[ 16 ]} which considers the electrical property of a composite material as a resistance network made up of three kinds of series-parallel connected resistors, corresponding to the transport in grains, at grain boundaries, and at the surface, as shown in Fig.  5 . In this model, the grain size and the volume ratio of both the main phase and the dispersed phase are considered. However, in a real system, the dispersion of the two phases is not ideally uniform. As a result, Uvaron proposed a modified morphology model, based on Dudney’s resistance network model, in which the agglomeration, homo-dispersion, and other dispersion state were considered (see Fig.  6 ). ^{[ 17 ]}

Fig. 3.

	Figure Option View Download New Window
	Fig. 3. The conductivity of LiI–Al 2 O 3 as a function of Al 2 O 3 content. [ 13 ]

Fig. 4.

	Figure Option View Download New Window
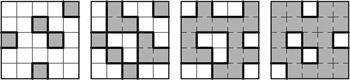	Fig. 4. Percolation model of an ionic conductor at different concentrations dispersed in insulating material. Insulator is shown in gray and ionic conductor is shown in white. [ 14 , 15 ]

Fig. 5.

	Figure Option View Download New Window
	Fig. 5. The resistance network model. [ 16 ]

Fig. 6.

	Figure Option View Download New Window
	Fig. 6. Morphology model for composite electrolyte. [ 17 ]

Batteries with hybrid electrolytes are considered to be the next generation for large-scale energy storage. ^{[ 18 , 19 ]} In a hybrid electrolyte battery, a solid-state electrolyte is used to separate the battery into two compartments of cathode and anode in the presence of a liquid electrolyte. During charge and discharge, the ions diffuse and migrate across the solid electrolyte and electrochemical reactions take place at the electrodes. Understanding the lithium-ion diffusion mechanism between the liquid electrolyte and the solid electrolyte is highly important for the improvement of such batteries’ performance. ^{[ 20 , 21 ]} The migration of ions across the interface between the liquid and solid electrolytes includes: (i) absorption of solvated ions on the surface of solid electrolyte, (ii) desolvation of lithium ions, (iii) hopping of lithium ions into the lattice of the solid electrolyte, and (iv) migration of lithium ions from the outer surface into the inner part of the solid electrolyte. The factors influencing the dynamic properties of lithium-ion diffusion in this model include: (i) absorption energy of solvated ions on the surface of solid electrolyte, (ii) desolvation energy, and (iii) surface structure of the solid electrolyte. ^{[ 22 ]} The thermodynamics of ion transport across the interface was investigated by Ogumi using a symmetric cell, and it was found that the desolvation process of ions had higher energy than the other processes. ^{[ 20 , 22 , 23 ]} The interaction between ions and solvent molecules affects the dynamics of ion migration across the interface. In high concentration propylene carbonate (PC) solution, a strong interaction exists between lithium ions and solvent molecules, making the desolvation process the rate-determining step.

Composite electrolytes of polymer and inorganic materials are very safe and flexible, and can be made compatible with existing battery structures and the means of fabrication. Therefore, composite solid electrolytes are very promising candidates for the next generation of solid-state batteries. ^{[ 1 , 24 ]} A polymer electrolyte was first reported in 1975 by Wright et al. ^{[ 25 ]} Later on, Wieczoreck found that conductivity was increased by adding inorganic particles into the polymer electrolyte. ^{[ 26 ]} The inorganic filler lowered the glass transition temperature and prevented crystallization of the polymer, leading to an increase in conductivity. ^{[ 27 ]} Scrosati proposed that ion diffusion at the interface also contributes to an increase in conductivity. ^{[ 28 ]} Interactions between functional groups on the surface of inorganic materials and those on the surface of polymers are shown in Fig.  7 . The surface interaction and structural modification result in an increase in charge carrier concentration, making both the conductivity and transference number higher. Mellander further proposed that the surface functional groups of inorganic materials have a Lewis acid character, so they can act as hopping sites for ion diffusion. ^{[ 29 ]} As a result, the total conductivity of the material can be improved by structural modification at the interface.

Fig. 7.

	Figure Option View Download New Window
	Fig. 7. Diagram showing the interaction of polymer electrolyte and inorganic materials with different surface functional groups. [ 28 ]

Several different polarization mechanisms are found in materials: electronic displacement polarization, ionic displacement polarization, orientation polarization, and interfacial polarization as shown in Fig.  8 . ^{[ 33 – 35 ]} Each type of polarization has characteristic relaxation time as demonstrated in Fig.  9 . Impedance spectroscopy is a time domain method; therefore, different polarization mechanisms can be distinguished by using IS.

Fig. 8.

	Figure Option View Download New Window
	Fig. 8. Four polarization mechanisms in materials. [ 34 , 35 ]

Fig. 9.

	Figure Option View Download New Window
	Fig. 9. Characteristic relaxation frequency ranges of the four polarization mechanisms. [ 36 , 37 ]

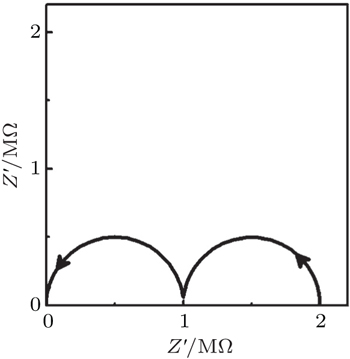
The impedance properties of materials can be understood with the help of an equivalent circuit, which has the same impedance response. For example, a typical impedance spectrum of a ceramic electrolyte contains two responses, one from the grains and the other from the grain boundaries, as shown in Fig.  10 . The corresponding equivalent circuit is illustrated in Fig.  11 . The impedance of grains and grain boundaries can be represented separately by RC parallel circuits, which have different characteristic time constants ( t = RC ). Electrical properties ( R , C ) of grains and grain boundaries can be obtained from the equivalent circuit. According to the brick layer model, the two semicircles of a ceramic can be identified based on the capacitance. The typical capacitance for bulk is 10 ^–12  F, and the typical capacitance for grain boundaries is 10 ^–11 –10 ^–8  F. ^{[ 38 ]}

Fig. 10.

	Figure Option View Download New Window
	Fig. 10. Typical impedance spectrum of an inorganic solid electrolyte.

Fig. 11.

	Figure Option View Download New Window
	Fig. 11. Equivalent circuit of an inorganic solid electrolyte. 1 and 2 represent different conductivity regions.

Several different representations for impedance data, i.e., impedance, inductive, modulus, and permittivity, are shown in Table  2 . ^{[ 12 ]} The combination of the different representations is beneficial to impedance analysis. According to the effective medium model for a heterogeneous system containing two phases, if one phase has a low volume fraction and low conductivity, two separate responses can be found in the impedance (Fig.  12(a) ). However, we can only observe one apparent response in the impedance plot of M * because there is a large difference between the two capacitances. If one phase has a low volume fraction but high conductivity, the capacitance values will be similar and there will be a large difference in resistance. As a consequence, only one apparent response can be found in the impedance plot of Z *, and two responses can be observed in the impedance plot of M *, as shown in Fig.  13 . Therefore, in order to get complete information on a material, the impedance data should be analyzed using different representations simultaneously. ^{[ 38 – 40 ]}

Fig. 12.

	Figure Option View Download New Window
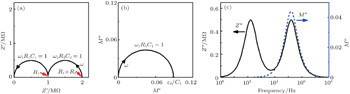	Fig. 12. Nyquist plot of Z * (a), Nyquist plot of M * (b), and Bode plot of Z ″ and M ″ (c), for the equivalent circuit in Fig.  11 ( R 1 = R 2 = 1 × 10 6  Ω, C 1 = 1 × 10 –12  F, C 2 = 1 × 10 –9  F).

Fig. 13.

	Figure Option View Download New Window
	Fig. 13. Nyquist plot of Z * (a), Nyquist plot of M * (b), and Bode plot of Z ″ and M ″ (c), for the equivalent circuit in Fig.  11 ( R 1 = 1 × 10 8  Ω, R 2 = 1 × 10 6 Ω, C 1 = C 2 = 1 × 10 –12  F).

Table 2.

Table 2.

Table 2. Different representations for impedance data. μ = jωC c , where C c is the capacitance of an empty cell. . M Z Y ε M M μZ μY –1 ε –1 Z μ –1 M Z Y –1 μ –1 ε –1 Y μM –1 Z –1 Y με ε M –1 μ –1 Z –1 μ –1 Y ε

Table 2. Different representations for impedance data. μ = jωC c , where C c is the capacitance of an empty cell. .

Nuclear magnetic resonance is a powerful experimental technique for studying diffusion. For non-ionic conductors, NMR shows a Gaussian distribution. For superionic conductors in which ions can transport in a long range by fast hopping through adjacent lattice sites, NMR gives a Lorentz distribution with a narrow width. ^{[ 41 ]} Heitjans investigated lithium diffusion in Li ₂ O using NMR. When the crystal size of Li ₂ O was decreased down to the nano-scale, the NMR spectrum showed a new narrow Lorentz-like peak, indicating that the ions at the interface of nano-scale polycrystalline Li ₂ O had faster motion than the ions in the inner grains. ^{[ 42 ]} Similar phenomena were also observed in nano-scale LiNbO ₃ , LiTiO ₃ , and other materials. ^{[ 43 , 44 ]} For Li ₂ O–Al ₂ O ₃ composite, NMR spectra suggested an overlap of Gaussian and Lorentz peaks, as shown in Fig.  14 . ^{[ 45 , 46 ]} Because Al ₂ O ₃ is a lithium-ion insulator, the new narrow Lorentz peak must come from the interface between Li ₂ O and Al ₂ O ₃ , indicating a fast ionic transport at the interface. ^{[ 45 ]}

Fig. 14.

	Figure Option View Download New Window
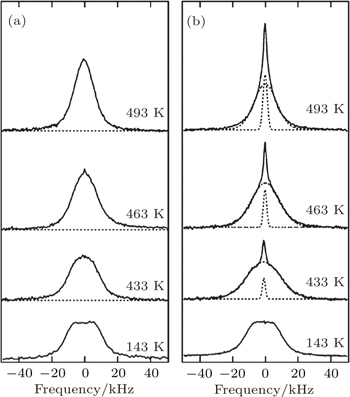	Fig. 14. 7 Li NMR spectra ( ν = 58.3 MHz) at various temperatures of the (a) micro- and (b) nano-crystal composite 0.5Li 2 O·0.5Al 2 O 3 . [ 42 , 45 ]

In addition to the effect on the width of NMR spectra, fast transport of ions in materials also influences the relaxation process, including spin–lattice relaxation ( T ₁ ), spin–spin relaxation ( T ₂ ), and spin–lattice relaxation in a rotating coordinate system ( T _1p ). ^{[ 32 , 41 , 46 ]} As shown in Fig.  15 , the atoms in grains in Li ₂ O–Al ₂ O ₃ composite show a different spin-lattice relaxation time from the atoms at the interface. With an increase in temperature and insulator content x , much slower decay was observed. The fast decay can be attributed to the less mobile ions in grains, and the slow decay can be attributed to the highly mobile ions in the interfacial regions. Therefore, different dynamic information about ion diffusion can be obtained. ^{[ 45 ]}

Fig. 15.

	Figure Option View Download New Window
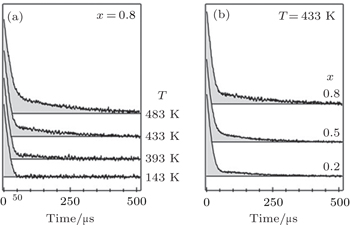	Fig. 15. 7 Li nuclear magnetic resonance (NMR) free induction decays of nanocrystalline (1 – x )Li 2 O: x Al 2 O 3 composites recorded at 58.8 MHz at different temperatures ( T is temperature and x is Al 2 O 3 content). [ 45 ]

The development of solid electrolytes is crucial to the next generation of very safe solid-state batteries. In addition to optimization of crystal structures, fast interfacial diffusion is another new direction for designing novel electrolyte materials. The concept “nanoionics” has been proposed. ^{[ 49 , 50 ]} When the particle size of a material with fast interfacial diffusion is nano-scale, the high volume percentage of the interface may increase the total conductivity of the material.

During decades of research on lithium-ion batteries, the structural evolution of cathode materials, ion diffusion in lattice, and electrochemical processes have been studied extensively. However, our knowledge of interfacial diffusion is insufficiently detailed, limiting the development of advanced battery technologies. To significantly improve batteries, high performance electrolytes with good overall properties, such as high conductivity, wide electrochemical window, good safety, great stability in a wide temperature range and good mechanical properties, are required. ^{[ 51 , 52 ]} Since including all the properties in one material is a big challenge, it is necessary to develop a composite electrolyte by combining different existing electrolytes – solids, polymers, and liquids. ^{[ 53 , 54 ]} As interfacial transport plays a major role in the diffusion of ions, understanding the physical mechanisms of ion diffusion at a multiphase interface will greatly help the designers of a new composite electrolyte.

High energy density is one of the most important requirements for commercial applications of batteries. ^{[ 55 ]} In order to improve the energy density and power density of batteries, the optimization of electrode structure is necessary. The constituents in electrodes include active materials, electronic conducting additives, binders, and penetrating liquid electrolytes. Electrode materials are secondary particles composed of small primary crystals. The active material particles of electrodes are combined with conducting additives. A binder binds together all the electrode particles and additive particles. Ion diffusion in the electrode layer is not only a multiple-phase transport process, but also a multiple-scale transport phenomenon, including ion hopping in the lattice of the electrode material, ion diffusion among the primary crystals, ion diffusion at the interfaces of different phases (electrode particles, polymer binder, conducting additives, liquid electrolyte), and ion diffusion along macro pathways from the bottom of the electrode layer to the surface. ^{[ 56 ]} Understanding the complex transport process in an electrode layer will dramatically help design new electrode structures so that rate performance can be improved, the amount of non-active materials can be reduced and ultimately the energy density of the full battery can be increased.