† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11275064 and 11075050), the Specialized Research Fund for the Doctoral Program of Higher Education, China (Grant No. 20124306110003), and the Construct Program of the National Key Discipline, China.
We present a paradigmatic method for exactly studying non-Markovian dynamics of a multi-level V-type atom interacting with a zero-temperature bosonic bath. Special attention is paid to the entanglement evolution and the dynamical non-Markovianity of a three-level V-type atom. We find that the entanglement negativity decays faster and non-Markovianity is smaller in the resonance regions than those in the non-resonance regions. More importantly, the quantum interference between the dynamical non-Markovianities induced by different transition channels is manifested, and the frequency domains for constructive and destructive interferences are found.
Quantum non-Markovian dynamics, due to its wide existence in the quantum optical system, [ 1 ] quantum dot, [ 2 ] superconductor system, [ 3 ] quantum chemistry, [ 4 ] and biological system [ 5 ] and some possible applications in quantum metrology [ 6 ] and quantum communication, [ 7 – 10 ] has received much attention in recent years. Several proposals [ 11 – 17 ] for the measure of non-Markovianity have been presented and various dynamical properties [ 18 – 39 ] of non-Markovian processes have been investigated. Experimentally, the simulation of non-Markovianity [ 40 , 41 ] under controlled environments has been realized.
The nature of a quantum non-Markovian process is the flow of lost information from the environment back to the open system, which leads to the oscillations of some pivotal physical quantities such as quantum trace distance, [ 11 ] quantum correlation, [ 12 , 14 ] and quantum Fisher information. [ 13 ] Although the properties of these oscillations are not in complete agreement, each of them can serve as the signature of non-Markovian dynamics. We will study the dynamical non-Markovianity in terms of the entanglement negativity. [ 42 , 43 ]
The study of non-Markovian dynamics of open quantum systems is typically very involved. Most of the previous works about non-Markovian dynamics mainly concentrated on the two-level systems. The high-dimensional open quantum systems, especially the high-dimensional dissipative quantum systems, due to their complexity, have been seldom investigated. In this paper, we present a paradigmatic method for exactly studying the non-Markovian dynamics of a multi-level V-type atom decaying in a zero-temperature bosonic bath. As a special example, we will emphatically study the case of a three-level V-type atom. The evolution of entanglement, the non-Markovianity of the quantum process, and the interference effect between different transition channels will be the main contents investigated.
The paper is organized as follows. In Section 2, we introduce the microscopic model for a multi-level V-type atom interacting with a zero-temperature bosonic bath and present the schematic method for treating the problem. In Section 3 and Section 4, we study respectively the evolution of entanglement (measured by negativity) and the non-Markovianity of the dynamics for the special case of a three-level V-type atom. Finally, the conclusion is given in Section 5.
Consider an atom A embedded in a zero-temperature bosonic bath modeled by an infinite chain of quantum harmonic oscillators (see Fig.
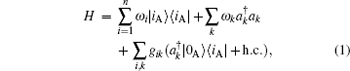
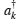
(a) Schematic diagram of the model. The atom A (main system) is embedded in a bosonic bath and entangled initially with another identical ancillary atom B. The total initial state is | Ψ (0)〉. (b) Energy levels of the multi-level V-type atom.
For the following study, we now assume another identical ancillary atom B which is free from the environment but initially entangled with atom A. The initial state of the two atoms plus the environment is assumed to be

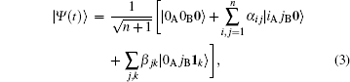
The state | Ψ ( t )〉 must satisfy the Schrodinger equation governed by Hamiltonian (1), which leads to the following equations about coefficients α i j ( t ) and β jk ( t ):
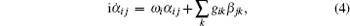
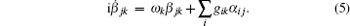

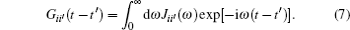
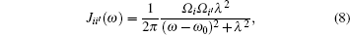
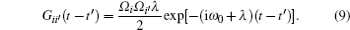
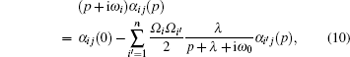
In this section, we take the three-level V-type atom as a paraphrastic example to demonstrate the procedure for exactly solving the dynamics. We study the entanglement evolution in terms of negativity. The time evolution of entanglement in a one-sided noisy environment is an important model, which may be used to simulate the procedure of a real entanglement distribution. Suppose Alice wants to establish an entanglement resource with distant Bob. She first produces a local entangled state of two atoms A and B, and then sends atom B to Bob through a quantum channel and keeps atom A in her hand. If we suppose only the sent atom suffered from noise, then the procedure corresponds to the time evolution of entanglement in a one-sided environment. The non-local entanglement of high-dimensional quantum systems is very relevant because of the security in quantum cryptography. [ 44 , 45 ]
Tracing over the bath degrees of freedom, from Eq. (

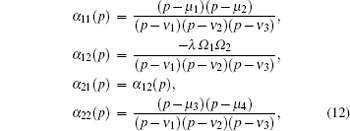
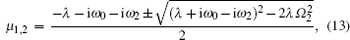
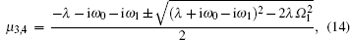
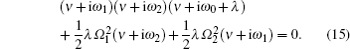
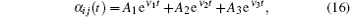
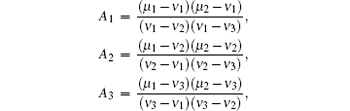
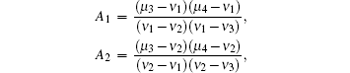

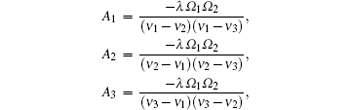
Secondly, let 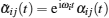
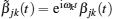
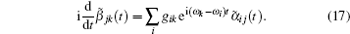
From Eq. (

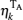
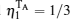

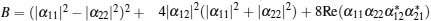
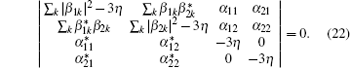
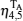
In Fig. Time evolution of negativity for (a) non-degenerate case with ω 1 = 5 Ω , ω 2 = 7 Ω , and ω 0 = 6 Ω , and (b) degenerate case with ω 1 = ω 2 = ω 0 = 6 Ω . 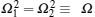
Figure (a) Time evolution of negativity for degenerate transition and for different detuning from the bath frequency, where ω 1 = ω 2 = 6 Ω , λ = 0.4 Ω , and the dimensionless detuning is defined by Δ = ( ω 0 − ω 1 )/ Ω . (b) A plane view.
In Fig. Time evolution of negativity for non-degenerate transition and for different detuning from the bath frequency, where ω 1 = 5 Ω , ω 2 = 7 Ω , and λ = 0.4 Ω .
We now discuss the interference between non-Markovianities induced by different transition channels. We will use the non-Markovian measure [ 12 ] based on the entanglement with an ancillary particle. Suppose a system of interest is initially prepared in a maximally entangled state with an ancillary particle, where only the system is influenced by a noise environment and the ancillary particle is noise-free. Then the quantity for measuring the non-Markovianity of the quantum process is defined as [ 12 ]
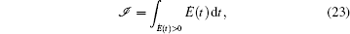
The main and ancillary systems in our problem are respectively atoms A and B, which are initially in the maximally entangled state given by Eq. (
In order to see the interference effect of non-Markovianity, we also plot the non-Markovianities that only the first transition channel ω 1 or only the second channel ω 2 is opened, i.e., corresponding to a two-level system (The red and green lines in Figs. Non-Markovianity as a function of the bath frequency with λ = 0.4 Ω : (a) ω 1 = 4 Ω , ω 2 = 8 Ω ; (b) ω 1 = 5 Ω , ω 2 = 7 Ω ; and (c) ω 1 = ω 2 = 6 Ω . The red (green) lines correspond to the non-Markovianity that only the first (second) transition exists and the black lines are the their sum. Note that the red and green lines in panel (c) overlap completely and the green line is omitted. The bar charts correspond to the non-Markovianity of the real three-level atom.
We have presented a paradigmatic method for exactly studying non-Markovian dynamics of a multi-level V-type atom interacting with a zero-temperature bosonic bath. For the special case of a three-level V-type atom, the exact analytical expressions for entanglement negativity have been obtained and the dynamical non-Markovianity has been investigated. We have found that the entanglement negativity decays faster and non-Markovianity is smaller in the resonant or quasi-resonant regions compared with that in the non-resonant case. In addition, narrower spectral width is beneficial for improving the dynamical non-Markovianity and preventing the decay of entanglement. These properties are similar to those in the open two-level quantum systems. A distinctive phenomenon observed in the case of three-level V-type atoms is the quantum interference between the non-Markovianities induced by different transition channels. We have demonstrated the constructive and destructive interferences and the corresponding frequency domains for the two kinds of interferences.
Quantum correlation and interference are very important phenomena in quantum physics. Our method for exactly solving dynamics applies in principle to the case of more higher-dimensional open quantum systems, particularly suitable for the numerical simulation of high-dimensional open systems. We expect that non-Markovian dynamics of high-dimensional open quantum systems will show richer features.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 |


