In a recent paper, ^[1] we have pointed out that an initial number state | l⟩ ⟨ l| undergoing through a diffusion channel, described by the master equation^{[2, 3]}

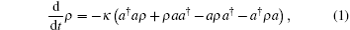
would become a new photon optical field, named the Laguerre-polynomial-weighted chaotic state, whose density operator is

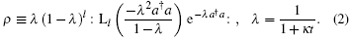
Here ∷ is the normal ordering symbol, 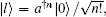and L_l is the Laguerre polynomial. Experimentally, this new mixed state may be implemented, i.e., when a number state enters into a diffusion channel. Remarkably, this state possesses photon number Tr(a^† aρ ) = l + κ t at time t, so we can control the photon number by adjusting the diffusion parameter κ ; this mechanism may have applications in quantum controlling.

To go a step further, we derive the evolution law of a negative binomial state (NBS) in a diffusion channel in this paper. Physically, when an atom absorbs some photons from a thermo light beam, the corresponding photon field will be in a negative binomial state. We are thus challenged by the questions: how an initial NBS evolves in a diffusion channel, what is the final state, and what is the photon number distribution in the final state. To the best of our knowledge, such questions have not been touched on in the literature before.

Our paper is arranged as follows. In Section 2, we convert the density operator of NBS into the normally ordered form. In Section 3, based on the Kraus-operator solution corresponding to the diffusion channel, we find the evolution law of NBS in the diffusion channel. Then in Section 4, we calculate the photon number distribution in the final state.

Corresponding to the negative-binomial formula

there exists a negative-binomial state of quantum optical field^[4]

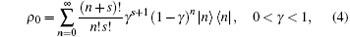
where is the Fock state, a^† is the photon creation operator, and | 0⟩ is the vacuum state in the Fock space. NBS is intermediate between a pure thermal state and a fully coherent state, and its nonclassical properties and algebraic characteristics have already been studied in detail in Refs.  [5] and [6]. The photon number average in this state is

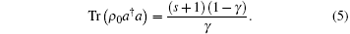
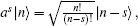
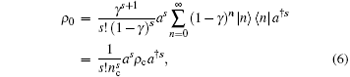
Using [a, a^† ] = 1 and one can reform Eq.  (4) as

where ρ _c denotes a chaotic field

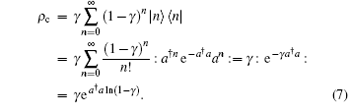
Equation  (6) tells us that when some photons are detected for a chaotic state, e.g., after detecting several photons, the chaotic light field exhibits a negative-binomial distribution. One can further show TrΣ _c = 1, and

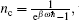
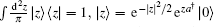
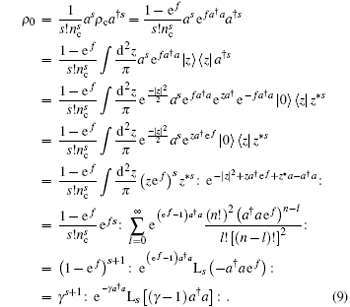
is the mean number of photons in the chaotic light field. According to the Bose– Einstein distribution, where β = 1/(k_BT), k_B is the Boltzmann constant, and ω is the frequency of the chaotic light field. We can derive the normally ordered form of the density operator of NBS. Let ln(1 − γ ) = f, then n_c = e  ^f/(1 − e  ^f). By introducing the coherent state representation and employing the technique of integration within an ordered product (IWOP) of operators, ^{[7, 8]} we reform Eq.  (6) as

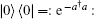
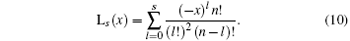
where we have used and the definition of Laguerre polynomials

Equation  (9) is quite different from Eq.  (1), so they represent different optical fields.

In Ref.  [9], by using the entangled state representation and the IWOP technique, we have derived the infinite sum form of ρ (t)

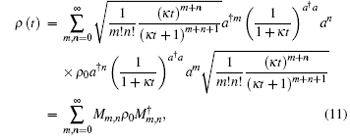
where

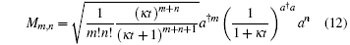
satisfies 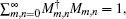and is trace conservative.

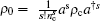
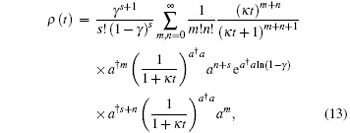
Now we examine the time evolution of the negative binomial optical field in a diffusion channel. Substituting into Eq.  (11), we have

in which we first consider the summation over n. Using

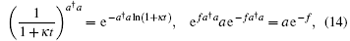
we have

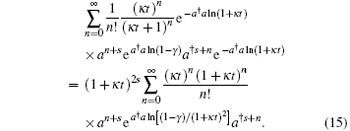
From Eq.  (9), we have

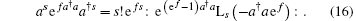
It follows

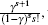
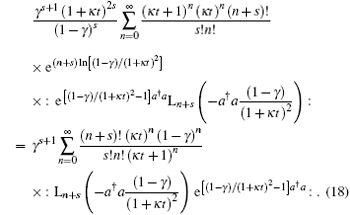
Substituting Eq.  (17) into Eq.  (15) and multiplying we obtain

Then using the new generating function formula about the Laguerre polynomials^[10]

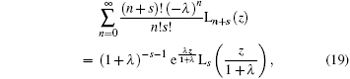
we obtain

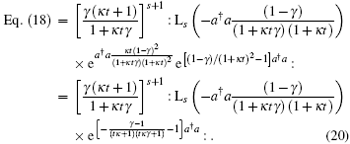
For ρ (t) in Eq.  (13), we need to perform the summation over m. Using the summation technique within normal ordering, we have

where

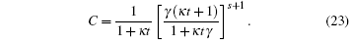
Comparing ρ (t) in Eq.  (21) with ρ ₀ in Eq.  (9), we can see the big difference. Now we must check if Trρ (t) = 1. In fact, using the coherent state’ s completeness relation and

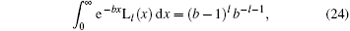
we do have

Now we evaluate the photon number average in the final state. Using Eqs.  (10) and (21)– (24), we have

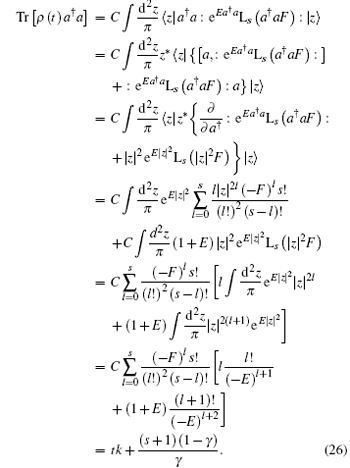
Comparing with Eq.  (5), we find that after passing through a diffusion channel, the photon average of NBS varies from (s + 1) (1 − γ )/ γ to tk + (s + 1) (1 − γ )/ γ ,

This result is encouraging, since by adjusting the diffusion parameter κ , we can control the photon number. When κ is small, it slightly increases by an amount of κ t. Therefore, the diffusion process of NBS can be considered as a quantum controlling scheme through photon addition.