†Corresponding author. E-mail: weiliu.sd.china@hotmail.com
This paper studies the distributed H∞ control problem of identical linear time invariant multi-agent systems subject to external disturbances. A directed graph containing a spanning tree is used to model the communication topology. Based on the relative states of the neighbor agents and a subset of absolute states of the agents, distributed static H∞ controllers are proposed. The concept of an H∞ performance region is extended to the directed graph situation. Then the results are used to solve the leader–follower H∞ consensus problem. Sufficient conditions are proposed based on bounded real lemma and algebraic graph theory. The effectiveness of the theoretical results is illustrated via numerical simulations.
Recently, the distributed control problem of multi-agent systems has drawn great attention for its broad potential applications in many areas such as formation control, [1– 4] flocking control, [5] and consensus control.[6, 7] Compared with traditional control systems, agents in the multi-agent systems are coupled through networks which are usually modeled by directed or undirected graphs. The system behavior depends not only on the individual agent dynamic, but also on the structure of the networks.[7] Due to some physical constrains such as limited resources and energy or short communication ranges, individual agent cannot obtain the global information of the system. Thus, only distributed controllers can be used with local information of neighbor agents. The distributed controllers have many advantages such as flexible scalability, high robustness, and low costs. It has been studied from different perspectives and numerous results have been obtained.
In Ref. [1], Jadbabaie et al. considered the coordination problem of groups of mobile autonomous agents and provided a theoretical explanation for the observed behavior of the Vicsek[6] model. Based on algebraic graph theory, Fax and Murry analyzed the formation stability under directed communication topologies.[2] In Ref. [5], a theoretical framework for the design and analysis of distributed flocking algorithms was presented by Olfati-Saber. In Ref. [7], Ren and Beard proved that the consensus of a single integrator dynamic could be achieved if the union of the directed interaction graphs had a spanning tree. A consensus of general linear invariant dynamics was studied with static feedback controllers in Refs. [8]– [10]. An observer-type dynamic consensus protocol was proposed by Li et al. in Ref. [11] and the concept of a consensus region was introduced. In Ref. [12], a decomposition approach was used to study the H∞ control problem of identical dynamically coupled systems subject to external disturbances. Under undirected graphs, based on local relative output information, Li et al. proposed dynamic H∞ controllers.[13] As an extension of consensus regions, Li et al. introduced the notions of the H∞ and H2 performance regions under undirected graphs and proved that the unbounded H∞ performance region was independent of the communication topology as long as it was connected.[14] In Ref. [15], Wang et al. proposed a control protocol to solve the H∞ consensus problem synthesized with transient performance. In Refs. [16] and [17], the H∞ consensus problems of multi-agent systems subjected to external disturbances were solved under directed strongly connected topologies. In Refs. [18]– [22], the leader– following tracking problems were also considered. However, until now, the H∞ control problems of general linear multi-agent systems with directed communication topology which just contains a directed spanning tree without the strongly connected condition have not been investigated.
In this paper, we investigate the distributed H∞ control problem of general identical linear time invariant multi-agent systems subject to external disturbances. A directed graph is used to model the communication topology. It is assumed that the directed graph has a spanning tree and there is at least one root node with a loop. Based on the local relative states information of the neighbor agents and a subset of absolute information of the agents, distributed H∞ controllers are constructed. Sufficient conditions are proposed based on the bounded real lemma and algebraic graph theory. Then the concept of H∞ performance regions proposed in Ref. [14] is extended to the directed graph situations. It is proved that the H∞ performance regions of multi-agent systems under directed communication topologies depend on both the communication topologies and system dynamics. Compared with the existing results in Refs. [13] and [14] where the communication topologies are assumed to be undirected and the results in Ref. [16] and [17] where the communication topologies are assumed to be strongly connected, the main contribution of this article is that the H∞ control problem is solved under directed communication topology which just contains a spanning tree. The conclusions obtained here can consider the results in Ref. [14] as a special case. Then the results are applied to solve the leader– follower H∞ consensus problem.
The remainder of the paper is organized as follows. In Section 2, some necessary concepts and the notation are introduced. In Section 3, the H∞ control problem of multi-agent systems subjected to external disturbances is addressed. In Section 4, the results are applied to solve the leader– follower H∞ consensus problem. In Section 5, a simulation example is presented. Section 6 is the conclusion.
In this paper, the following notations will be used. Rn× n and Cn× n denote the set of n× n real and complex matrices, respectively. For μ ∈ C, the real part is Re(μ ). ⊗ denotes the Kronecker product. In is the identity matrix of order n. For a square matrix A, λ (A) denotes the eigenvalues of matrix A, and 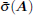
A directed graph 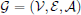
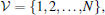

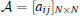

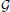
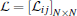
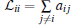
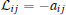

Lemma 1 (bounded real lemma[23]) For a positive scalar γ > 0 and the transfer function G(s) = C(sI − A)− 1B + D, then the following are equivalent:
(i) Re(λ (A)) < 0 and ∥ G (s)∥ ∞ < γ .
(ii) 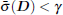
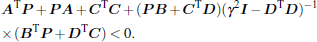
Lemma 2 (Schur complement lemma[24]) Given a matrix 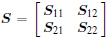
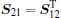
(i) S < 0.
(ii) 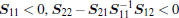
(iii) 
Lemma 3[25] Suppose that the eigenvalues of A ∈ RN× N have positive real parts, then there exists a positive definite matrix Q > 0 such that ATQ + QA > 0.
Consider a multi-agent system composed of N agents with identical general linear time invariant dynamics
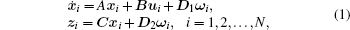
where xi(t) ∈ Rn, ui(t) ∈ Rp, and ω i(t) ∈ L2[0, ∞ ) are the state, the control input, and the external disturbance, respectively. zi ∈ Rq is the performance variable. A, B, C, D1, and D2 are constant system matrices with compatible dimensions. It is assumed that (A, B) is stabilizable, and (A, C) is detectable. Here, a directed graph 
Assumption 1 The directed graph 
Based on this assumption, the following distributed static consensus controller is proposed:
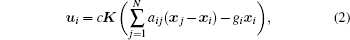
where K ∈ Rp× n is the feedback matrix to be designed, c is the coupling strength to be selected, and aij are the elements of the adjacency matrix of the communication topology. gi = 1 means that the agent i knows its own absolute state information; gi = 0, otherwise. Then, according to Assumption 1, 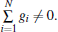
Then, the closed-loop system dynamics (1) using the controller (2) is
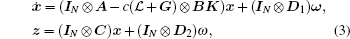
where 
Lemma 4[7] Zero is a simple eigenvalue of 

Remark 1 If the graph is assumed to be directed and strongly connected or undirected and connected, every agent can be seen as a root node. Furthermore, if 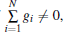

Lemma 5 Under Assumption 1, there exists a positive definite matrix Q and a positive scalar α such that

where 
Proof According to Lemma 4, one can obtain that 
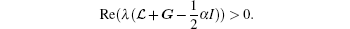
Thus, by Lemma 3, there exists a positive definite matrix Q such that 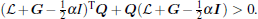
Definition 1 The suboptimal H∞ control problem of system (1) is said to be solved under the controller (2) with a given allowable 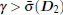
(i) The system is asymptotically stable.
(ii) The H∞ norm of Tω z is less than γ , i.e., ∥ Tω z∥ ∞ < γ .
Theorem 1 The suboptimal H∞ control problem of multi-agent system (1) with the controller (2) is solved with disturbance attenuation 
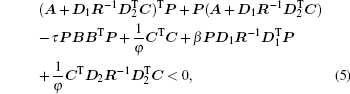
where 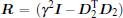
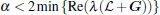
Proof According to bounded real lemma, if there exists a positive definite matrix 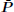
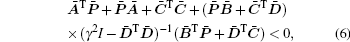
where 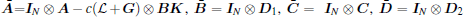

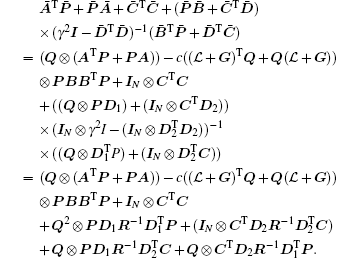
From Lemma 5, one has

where 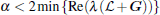
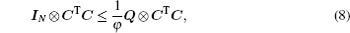
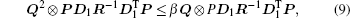
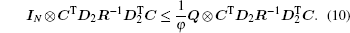

Since cα ≥ τ , then inequality (5) implies that inequality (6) holds. Thus, the H∞ control problem for system (1) is solved.
Remark 2 Note that the Laplacian matrix of a directed graph is not symmetric. Thus, the similarity transformation employed in Ref. [14] is not applicable here. We chose to solve the H∞ control problem directly using the bounded real lemma. From the proof of Theorem 1, we can see that the key tools leading to the above results rely on Lemma 5 and the properly designed matrix P̄ .
Remark 3 In Ref. [14], the notion of H∞ performance regions is introduced under undirected communication topologies to evaluate the performance of a multi-agent network subject to external disturbance. It is proved that the unbounded H∞ performance region is independent of the communication topology 
Remark 4 Under Assumption 1, if the communication topology is modeled by an undirected graph, matrix 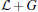

This conclusion is consistent with the existing results in Ref. [14]. Thus, the conclusion obtained here can consider the results in Ref. [14] as a special case. Furthermore, according to Remark 1, if the directed graph is assumed to be strongly connected, the topologies assumption in Assumption 1 can be relaxed so that there is at least one node with a loop.
Similar to Ref. [14], for a given graph, the H∞ performance limit can be obtained by the following corollary.
Corollary 1 Given a directed graph 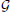
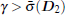
In this section, the leader– follower H∞ consensus problem is discussed. The followers’ dynamics are described in (1). The leader’ s dynamics is described as
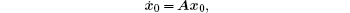
where x0 ∈ Rn, and A is the same as the followers’ . Here, we define the consensus performance variable as
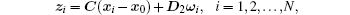
where zi ∈ Rp, and C is a constant matrix such that (A, C) is detectable.
The following distributed consensus controllers are proposed as:

where K is the feedback gain matrix to be designed. hi = 1 if agent i can obtain the leader’ state information; hi = 0, otherwise.
Then the closed-loop dynamics can be written as
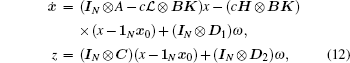
where 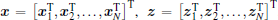
Definition 2 Given a positive scalar γ > 0, the leader– follower H∞ consensus problem of system (12) is said to be solved, if the following requirements are satisfied.
(i) If ω i ≡ 0, leaders– follower consensus is achieved, i.e., 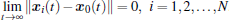
(ii) Under the zero-initial conditions, the H∞ norm of T̂ ω z is less than γ , i.e., ∥ T̂ ω z ∥ ∞ < γ .
Under the leader– follower structure, we need the following assumption.
Assumption 2 The graph has a spanning tree and at least one root agent has access to the leader.
Let x̂ i = xi − x0, then the closed-loop dynamics with the controller (12) can be rewritten as
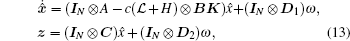
where 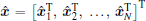
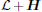
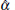

where 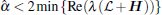
Until now, the leader– follower H∞ consensus problem has been converted to an H∞ control problem. Thus, a similar conclusion can be obtained.
Theorem 2 The leader– follower H∞ consensus problem is solved with disturbance attenuation 

where 
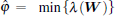
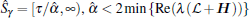
In this section, we provide some examples to illustrate the effectiveness of the above theoretical results. A multi-agent system consisting five agents is considered. The system matrices are defined as
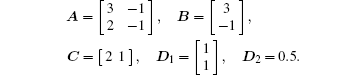
The external disturbance is defined as 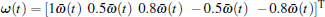
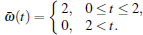
Example 1 In this example, the distributed H∞ control problem is considered. The directed communication topology is given in Fig. 1(a). Clearly, the communication topology has a directed spanning tree. Agents 1 and 5 are the roots, and agent 1 can obtain its own absolute state information. The Laplacian matrix of communication topology is
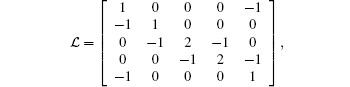
and G = diag{1, 0, 0, 0, 0}. The real part of the smallest eigenvalue of 

Thus, β = max {λ (Q)} = 21.5845, and φ = min {λ (Q)} = 0.0921. Set γ = 2 and τ = 1. Solving inequality (5), we obtain a feasible solution
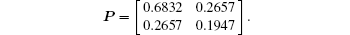
According to Theorem 1, the feedback matrix and coupling stength can be chosen as K = [1.7839 0.6025] and c = 1.6062, respectivly. The H∞ performance region is [1.5062, ∞ ).
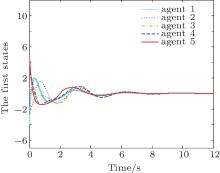
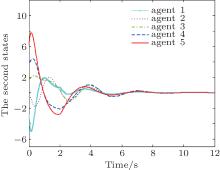
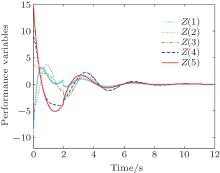
Figures 2 and 3 show the state trajectories of all the agents. Figure 4 shows the trajectories of the performance variables Zi with external disturbances. It is shown that states of all the agents converge to zero.
Example 2 In this example, the leader– follower H∞ consensus problem is considered. The directed communication topology is given in Fig. 1(b). We can see that agents 1 and 2 can obtain the leader’ s information and agent 1 is the root. The Laplacian matrix is the same as example 1, and H = diag{1, 1, 0, 0, 0}. We can obtain a feasible solution of (14)
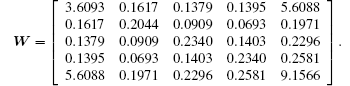
Thus, 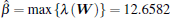
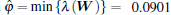
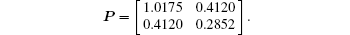
According to Theorem 2, the feedback matrix and coupling stength can be chosen as K = [1.4171 0.3962] and c = 1.6062, respectivly.
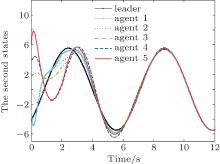
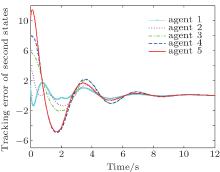
Figures 5 and 6 show the state trajectories of the leader and follower agents. Figures 7 and 8 show the trajectories of the tracking error. Note that the tacking error converges to zero, and all follower agents can track the leader’ s path.
In this paper, the distributed H∞ control problems of multi-agent systems subject to external disturbances have been investigated under directed communication topologies which have a spanning tree. Based on relative states of the neighbor agents and a subset of absolute information of the agents, local H∞ controllers have been designed. The concept of an H∞ performance region has been analyzed. It has been proved that, under directed networks, the H∞ performance region depends on both the communication topology and system dynamics. Finally, the results have been applied to deal with the leader– follower H∞ consensus problem.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|