†Corresponding author. E-mail: feichen@xmu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 61473240).
This paper considers the formation tracking problem under a rigidity framework, where the target formation is specified as a minimally and infinitesimally rigid formation and the desired velocity of the group is available to only a subset of the agents. The following two cases are considered: the desired velocity is constant, and the desired velocity is time-varying. In the first case, a distributed linear estimator is constructed for each agent to estimate the desired velocity. The velocity estimation and a formation acquisition term are employed to design the control inputs for the agents, where the rigidity matrix plays a central role. In the second case, a distributed non-smooth estimator is constructed to estimate the time-varying velocity, which is shown to converge in a finite time. Theoretical analysis shows that the formation tracking problem can be solved under the proposed control algorithms and estimators. Simulation results are also provided to show the validity of the derived results.
Multi-agent systems have attracted much attention in recent years. They offer many advantages over single agent systems, such as efficiency, robustness, scalability, versatility, adaptability, and lower cost.[1] A considerable amount of research effort has been devoted to the distributed control of multi-agent systems. Examples of interesting research directions include consensus, [2– 4] formation control, [5– 7] coordinated tracking, [8, 9] flocking, [10, 11] and so on.
In the formation control problem, the agents are required to form a pre-defined formation shape, and then maintain the shape during translational or rotation movements. Rigid formation can keep the distance between any agent pair (the shape of the whole group) unchanged, which is not guaranteed by an arbitrary formation. Another feature of rigid formation is that it can be used to stabilize the distances between all of the agent pairs while employing the information of only a few agent pairs. This feature is of great significance in a large group of agents. Rigid formation control has found applications in various fields, including a wireless sensor network, surveillance, industrial processes, and so on.[1, 12, 13] The objective of rigid formation tracking is to stabilize the relative positions of the agents according to a target rigid formation, while the agents can at the same time track a desired velocity. The incorporation of the desired velocity in formation control gives the system an extra ability to suit a complicated environment. However, this also complicates the design and analysis of the control algorithm. This paper is interested in the formation tracking problem for multi-agent systems via a rigidity framework.
The are many studies in the literature of formation control. In Ref. [14], the global asymptotic stability of triangular formations is investigated. Local asymptotic stability of minimally infinitesimally rigid formations is analyzed by means of Lyapunov-based stability analysis.[15] In Ref. [16], a distributed coordinated tracking problem for multiple networked Euler– Lagrange systems is solved under the constraint that the leader is a neighbor of only a subset of the followers. A distance-based formation maintenance controller is designed for cycle-free persistent formations under the condition that the velocity of the trajectory is sufficiently low.[17] For multi-agent formation maintenance and target tracking, a control law is developed in Ref. [7], where the desired translational velocity and the leader’ s relative position and velocity are required by all of the followers. Using the relative positions of all of the agents, distance-based formation maintenance and target tracking schemes are solved by a modified gradient-of-potential-function law.[18] Reference [19] presents the design of control protocols and distributed observers for the leader-following formation control, which also deals with the formation as well as the tracking problem. In Ref. [20], the consensus problem with a periodic intermittent communication and fixed directed topology is investigated, and then the consensus algorithm is extended to solve the formation control problem as well as the consensus tracking problem with switching directed topologies. Graph theory is a natural tool to describe multi-agent formation, a detailed discussion on the rigid graph theory and its applications is given in Ref. [1].
The contributions of this paper are stated as follows. First, a desired group velocity is incorporated into the rigid formation control problem. When the desired velocity is time-varying, a distributed nonsmooth estimator is constructed to estimate the velocity and a Lyapunov function is provided to show the finite-time convergence of the estimator. Second, a formation acquisition term is derived from the rigidity matrix, which is used to solve the rigid formation control problem with the aid of the velocity estimator. Theoretical proofs are provided to show the convergence of the proposed formation control algorithms.
The rest of this paper is organized as follows. In Section 2, notation and mathematical preliminaries are presented. The formation control problem is defined in Section 3. Control algorithm design and stability analysis are presented in Sections 4 and 5, respectively, for the case of constant desired velocity and the case of time-varying desired velocity. Simulation results are given in Section 6. Finally, Section 7 summarizes the investigation.
Some basic knowledge on graph theory will be given in this section. An undirected graph is defined as 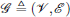
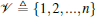
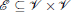
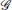
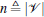
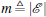
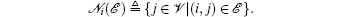
Let pi ∈ ℝ 2 be the position of vertex i. A formation can be denoted by a pair (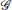
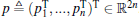
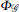
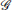
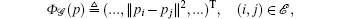
where ‖ · ‖ denotes the Euclidean norm. The rigidity of a formation is defined as follows.
Definition 1[6] A formation (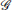
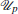

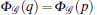
For a rigid formation, the distance between any two vertices will not change if the distances of the vertices corresponding to the edges which belong to the rigid graph remain unchanged during translation and rotation movements. The rigidity matrix R of a formation 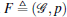
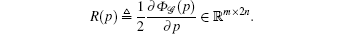
Obviously, the rigidity matrix only depends on the relative positions of the agents. Thus, we write the rigidity matrix as R(p̃ ) in the following, where p̃ ij = pi − pj, (i, j) ∈ ℰ . Based on the rank property of R (p̃ ), the infinitesimal rigidity of F is defined as follows.
Definition 2[6] A formation F = (
Typically, formations that are rigid but fail to be infinitesimally rigid have collinear or parallel edges. In the following, the minimal rigidity of a formation is introduced.
Definition 3[1] A formation is minimally rigid if it is rigid and no single interagent distance constraint can be removed without causing the formation to lose rigidity.
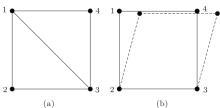
It can be verified that the graph in Fig. 1(a) is rigid. However, if any edge is removed from the graph, the graph is no longer rigid (see Fig. 1(b)). Thus, the graph in Fig. 1(a) satisfies Definition 3, and is said to be minimally rigid. In a two-dimensional space, a graph is minimally rigid if and only if m = 2n − 3.[1]
Lemma 1 If a real matrix A ∈ ℝ m× n has full row rank, then AAT is positive definite.
Proof For any x ∈ ℝ m, it follows that xT(AAT)x = (ATx)T(ATx) ≥ 0. In particular, if xT (AAT)x = 0, then ATx = 0. Because A has a full-row rank, the equation ATx = 0 has one and only one solution x = 0. That is, xT(AAT)x = 0 has one and only has one solution x = 0, which suggests that AAT is positive definite.
Consider a system of n agents governed by the single integrator dynamics
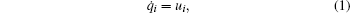
where 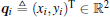
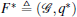

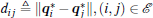
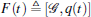
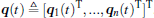
The objective of this paper is to design distributed controls ui based on local information such that,
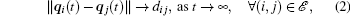
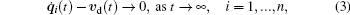
where υ d (t) ∈ ℝ 2 is any bounded, continuous function representing the desired velocity of the multi-agent system, and is available to only a subset of the agents.
In this section, we consider a case where the desired velocity vd is constant. Define the relative position of two agents as
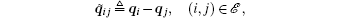
and let 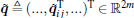
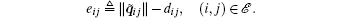
The dynamics of the distance error are
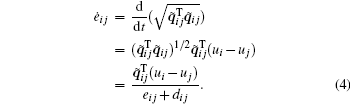
Define the following positive definite, radially unbounded function:
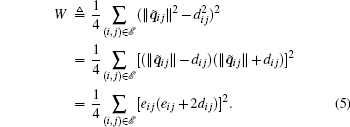
The derivative of Eq. (5) along Eq. (4) is given by
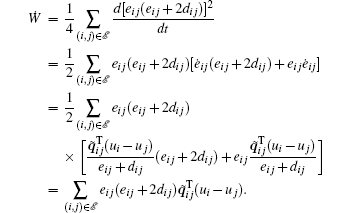
From the definition of R(q̃ ), we know that each row of R(q̃ ) consists of q̃ ij and q̃ ji. Thus, Ẇ can be written in a vector form as
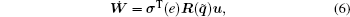
where 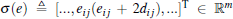
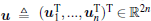
For each agent i, an estimator is designed to track the desired velocity vd
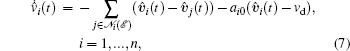
where 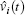
The control input u is then designed as
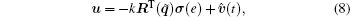
where 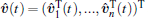
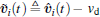
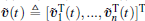
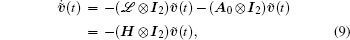
where ℒ is the Laplacian matrix associated with 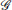
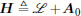
For a rigid graph, it is at least connected because otherwise if one or more nodes are not connected with other nodes, then this part of nodes can move freely without keeping distance to other nodes, which is in conflict with the nature of rigidity. Thus, 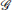
where k is defined in Eq. (8). Let 
where c is a sufficiently small positive number.
The main result of this section is stated in the following theorem.
Theorem 1 For system (1) under the control law (8) and the estimator (7), if F* is the desired formation and w(0) ∈ Ω (c), then the control objective (2) and (3) can be achieved, and the formation error and the estimation error converge to zero exponentially.
Proof The derivative of V along (6) and (9) is given by
Substituting Eq. (8) into Eq. (10) yields
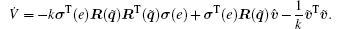
Because 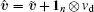
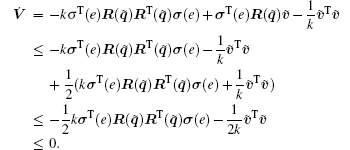
Because 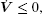
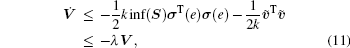
where inf(S) denotes the infimum of set S, and λ = min{2k inf(S), 1/λ max[(H ⊗ I2)− 1]}. λ max denotes the maximum eigenvalue. Thus, from Eq. (11), it follows that σ (e) = 0, 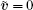
The exponential stability of 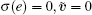
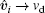
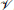
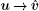
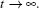

In this section, we consider a case where vd(t) is time-varying. It is assumed that the derivative of the desired velocity vd(t) is bounded, and this bound is denoted by γ .
Inspired by Ref. [8], the following non-smooth algorithm is proposed to estimate the time-varying desired translational velocity vd(t):

where 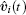
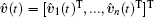
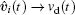
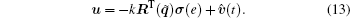
Theorem 2 For system (1) under the control law (13) and the estimator (12), if F* is the desired formation, w(0) ∈ Ω (c), and β > γ , then the control objective (2) and (3) can be achieved, and the formation error converges to zero asymptotically.
Proof In the following, we first prove that 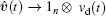
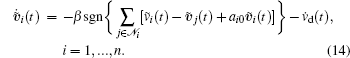
Rewrite Eq. (14) in a vector form as
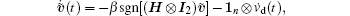
where sgn(x) = [sgn(x1), ..., sgn(xn)]T. Design the following Lyapunov function as:
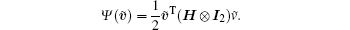
The derivative of 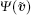
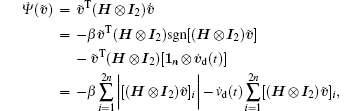
where 

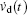
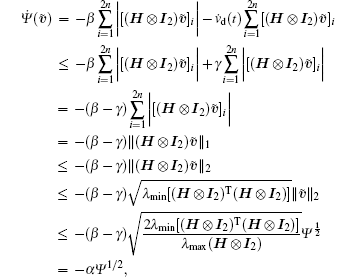
where 
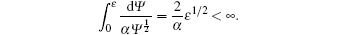
According to Theorem 3 in Ref. [22], we can conclude that 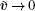
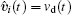
After time T, the control law of (13) becomes
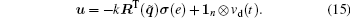
Substituting Eq. (15) into Eq. (6) yields
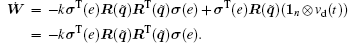
Following a similar proof to that of Theorem 1, it can be shown that R(q̃ )RT(q̃ ) is positive definite for w(0) ∈ Ω c. It thus follows that
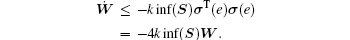
The rest of the proof is similar to that of Theorem 1, and is hence omitted.
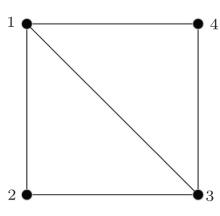
In this section, we present two simulation examples for the formation problem with constant and time-varying desired velocity, respectively. In both examples, we consider a group of four agents. The desired formation is a square shown in Fig. 2 where the agents are located at the four vertices. There are five edges in the graph. It can be verified that the formation given in Fig. 2 is minimally rigid. Let a10 = 1, a20 = a30 = a40 = 0. The desired distances between the agents are given by d12 = d23 = d34 = d41 = 10, 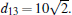

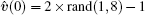
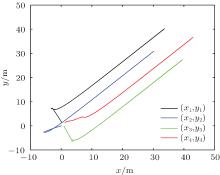
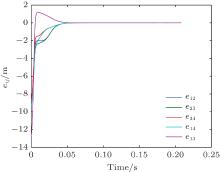
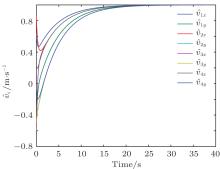
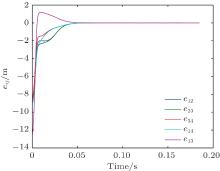
For the constant desired velocity case, let vd = 1. Figure 3 shows the agents’ trajectories, which shows that the agents can achieve the formation asymptotically. Figure 4 shows that the inter-agent distance errors converge to zero. Figure 5 describes the velocities of all of the agents which converge to the desired velocity vd = 1.
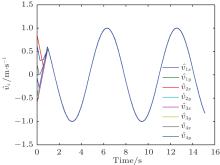
For the time-varying desired velocity case, let vd(t) = cos (t). Figure 6 shows that the agents can achieve the formation asymptotically. Figure 7 describes the inter-agent distance errors which converge to zero. Figure 8 shows the velocities of all the agents which converge to the given time-varying velocity vd(t) = cos (t).
In this paper, the distributed tracking problem of a minimally and infinitesimally rigid formation has been investigated. Two control algorithms have been designed to stabilize the inter-agent distances while allowing the formation to follow a constant or a time-varying velocity. In both cases, the desired trajectory velocity is assumed to be available to a subset of the agents. Distributed estimators have been constructed for each agent to estimate the desired velocity. The estimates are further employed to construct the control inputs of the agents where the rigidity matrix plays a central role. It has been proven that both the formation error and the estimator error can converge to zero. Finally, numerical examples have been proposed to verify the derived results.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|