†Corresponding author. E-mail: lansexiaoer@163.com
*Project supported by the Zhejiang Provincial Natural Science Foundation of China (Grant No. LQ13A010014) and the National Natural Science Foundation of China (Grant Nos. 11326164, 11401528, 11435005, and 11375090).
For the (2+1)-dimensional Broer–Kaup–Kupershmidt (BKK) system, the nonlocal symmetries related to the Schwarzian variable and the corresponding transformation group are found. Moreover, the integrability of the BKK system in the sense of having a consistent Riccati expansion (CRE) is investigated. The interaction solutions between soliton and cnoidal periodic wave are explicitly studied.
One knows that Painlevé analysis[1– 3] is effective for offering Bä cklund transformation (BT), Lax pair, Schwarzian forms, and exact solutions, etc. Furthermore, it is found that Painlevé analysis can also be used to obtain nonlocal symmetries. This type of nonlocal symmetries stems from the residue with respect to the singular manifold of the truncated Painlevé expansion and is also called residual symmetry.[4– 7] Since the residual symmetries are closely related to the Schwarzian form of the original differential system, one may localize them more easily than those coming from Darboux transformation (DT)[8– 12] and BT.[13, 14] Recently, by developing the truncated Painlevé expansion, Lou defined a new integrability in the sense of possessing a consistent Riccati expansion (CRE).[15] It has been revealed that many more integrable systems[15– 21] are CRE solvable. The CRE method is greatly valid for constructing both possible new integrable systems and various interaction solutions between different types of excitations. Some interesting exact solutions of nonlinear models are also shown in the recent literature.[22– 24]
In this paper, we concentrate on investigating the residual symmetries and CRE integrability of the (2+ 1)-dimensional Broer– Kaup– Kupershmidt (BKK) system, which have not yet been discovered. The BKK system reads

which may be derived from the inner parameter dependent symmetry constraint of the Kadomtsev– Petviashvili (KP) equation.[25] The Painlevé integrability and infinitely many symmetries of the system (1) were presented by Ruan and Chen.[26] Via the variable separation approach, Li[27] obtained rich continuous localized solutions and Lou[28] discussed its (2+ 1)-dimensional compact on solutions with and without completely elastic interaction properties.
This paper is organized as follows. In Section 2, from the truncated Painlevé expansion, the residual symmetry of the BKK system is obtained, based on which infinitely many nonlocal symmetries are also given. The nonlocal symmetry group is found by the localization process. In Section 3, the BKK system is verified CRE solvable and the soliton-cnoidal wave solutions are constructed. The last section contains discussion and a summary.
For the BKK system, we take a truncated Painlevé expansion
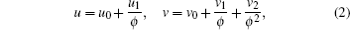
with u0, u1, v0, v1, v2, ϕ being the functions of x, y, and t.
Substituting Eq. (2) into Eq. (1) and vanishing all the coefficients of different powers of 1/ϕ , we have
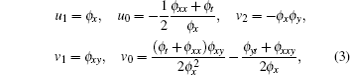
and the BKK system (1) is successfully reduced to its Schwarzian form
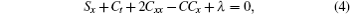
where λ is an arbitrary parameter. Here, we denote
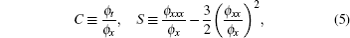
and they keep the Mö bious (conformal) invariance property

Due to above Mö bious invariance, a well-known fact is that ϕ possesses the following Lie point symmetry:
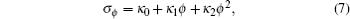
where κ 0, κ 1, and κ 2 are arbitrary constants.
From the above standard truncated Painlevé expansion Eq. (1), we have the following BT theorem and nonlocal symmetry theorem of Eq. (1).
Theorem 1 (non-auto-BT theorem) If the function ϕ satisfies Eq. (4), then
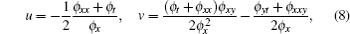
is just the solution of the (2+ 1)-dimensional BKK system (1).
Proof By direct verification.
Theorem 2 (nonlocal symmetry theorem) The BKK system (1) has the residual symmetry given by
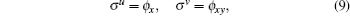
where u, v, and ϕ satisfy the non-auto BT Eq. (8).
Proof The symmetry equations of Eq. (1) read
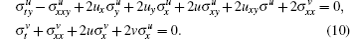
Substituting Eq. (9) into Eq. (10) and with the help of Eqs. (4) and (8), one finds that the symmetry equations (10) hold.
Actually, thanks to the arbitrary parameter λ in Eq. (4), we can present infinitely many nonlocal symmetries in two ways. One set of nonlocal symmetries for u and v is
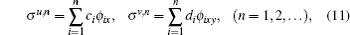
where every ϕ i satisfies Eq. (4) with λ = λ i and ci, di are all arbitrary constants. Another set of nonlocal symmetries for u and v reads

where ϕ (λ ) is the solution of Eq. (4).
To find out the symmetry group of the residual symmetry (9), i.e.,
one can solve the following initial value problem:
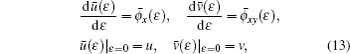
with ɛ being the infinitesimal parameter.
However, because of the intrusion of the function 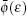

Now the nonlocal symmetry (9) of the original system (1) becomes a Lie point symmetry of the prolonged system including Eqs. (1), (8), and (14), saying

Correspondingly, the initial value problem (13) becomes
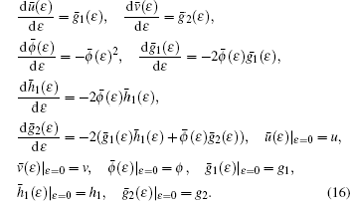
Then the solution of the initial value problem (16) leads to the following group theorem for the enlarged system.
Theorem 3 (group) If {u, v, ϕ , g1, g2, h1} is a solution of the prolonged system Eqs. (1), (8), and (14), so it is 

Theorem 3 shows that the residual symmetry (9) coming from the truncated Painlevé expansion is just the infinitesimal form of the group (17). Actually, the above group transformation is equivalent to the truncated Painlevé expansion (2) with Eq. (3) since the singularity manifold Eqs. (1), (8), and (14) are form invariant under the transformation
For the BKK system, we focus on its possible truncated Painlevé expansion solution in the form of

where R(w) is a solution of the Riccati equation

with b0, b1, b2 being arbitrary constants. By vanishing all the coefficients of the like powers of R(w) after substituting Eq. (18) with Eq. (19) into Eq. (1), we obtain
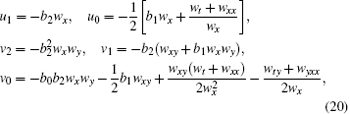
and the function w only needs to satisfy
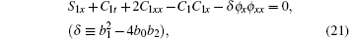
with
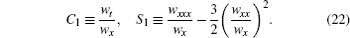
From above, it shows that the (2+ 1)-dimensional BKK system really has the truncated Painlevé expansion solution related to the Riccati equation (19). At this point, we call BKK system CRE solvable.[15]
In particular, the Riccati equation (19) has one solution R(w) = tanh(w), which converts the truncated expansion solution (18) into
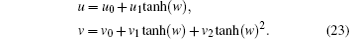
Due to the above consistent tanh-function expansion (CTE) (23), the BKK system is called CTE solvable. It is quite clear that a CRE solvable system must be CTE solvable, and vice versa. If a system is CTE solvable, some important explicit solutions, especially the interactions between soliton and other nonlinear waves, may be directly constructed. To leave this clear, we firstly give out the following non-auto BT.
Theorem 4 (BT) If w is a solution of Eq. (21) with δ = 4, then

is a solution of the system (1), where {u0, v0} is determined by Eq. (20) with b0 = 1, b1 = 0, and b2 = − 1.
Some nontrivial solutions of BKK system can be obtained from some quite trivial solutions of Eq. (21) by means of Theorem 4, which are listed as follows.
Example 1: Soliton solutions In Eq. (21), we take a quite trivial straight-line solution for w, saying
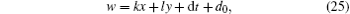
with k, l, d, d0 being arbitrary constants. Then substituting Eq. (25) into Theorem 4 yields the following kink soliton and ring soliton solution of the BKK system:
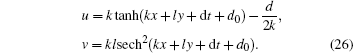
Example 2: Soliton-cnoidal waves To find out the interaction solutions between soliton and cnoidal periodic wave, let

where W1 ≡ W1(X) = WX satisfies
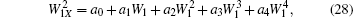
with a0, a1, a2, a3, a4 being constants. Substituting Eq. (27) with Eq. (28) into Theorem 4, we have the relations
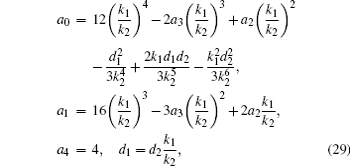
which lead to the following explicit solutions of Eq. (1) in the form of

Since W1 in Eq. (28) can be expressed as different types of Jacobi elliptic functions, the formula (30) exhibits the interactions between soliton and abundant cnoidal periodic waves. To show these soliton-cnoidal waves more intuitively, we just take a simple solution of Eq. (28) as
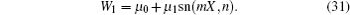
Substituting Eq. (31) into Eq. (28) with Eq. (29) yields
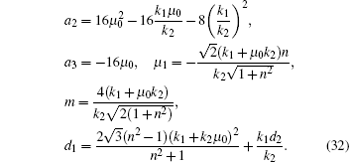
Hence, one kind of soliton-cnoidal wave solutions is obtained by taking Eq. (31) and
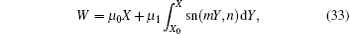
with the parameter requirement (32) into the general solution (30). Figure 1 displays this kind of soliton-cnoidal wave solutions, including the interaction of the kink soliton+ cnoidal periodic wave for u and the ring soliton+ cnoidal periodic wave for v at t = 0 respectively. The parameters used in the figure are selected as
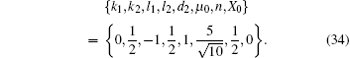
By developing the truncated Painlevé analysis, we investigate nonlocal symmetries and CRE integrability of the (2+ 1)-dimensional BKK system. The residual symmetry is found and thanks to the arbitrary parameter in the Schwartzian form of the BKK system, infinitely many nonlocal symmetries are also obtained. The nonlocal symmetry group is revealed by enlarging the original system to a larger one. Furthermore, the BKK system is proved CRE integrable. In particular, by means of the CTE, the general soliton-cnoidal wave solutions which may be explicitly expressed by the Jacobi elliptic functions and the corresponding elliptic integral are constructed. To leave it clear, we give out one type of kink soliton+ cnoidal periodic wave solution and ring soliton+ cnoidal periodic wave solution in graphical way. More types of these soliton-cnoidal wave solutions need our further study.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|



