Cite this Article
Hao Yan, Zhang Hong†, Cheng Xin-Lu. Path integral Monte Carlo study of (H2) n@C70 ( n = 1,2,3) . Chinese Physics B, 24(8): 088103  
Permissions
Path integral Monte Carlo study of (H2) n@C70 ( n = 1,2,3)
Hao Yana), Zhang Hong†b), Cheng Xin-Lua)
Institution of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China
College of Physical Science and Technology, Sichuan University, Chengdu 610065, China

†Corresponding author. E-mail: hongzhang@scu.edu.cn

*Project supported by the National Natural Science Foundation of China (Grant Nos. 11474207 and 11374217).

Abstract

The path integral Monte Carlo (PIMC) method is employed to study the thermal properties of C70 with one, two, and three H2 molecules confined in the cage, respectively. The interaction energies and vibrationally averaged spatial distributions under different temperatures are calculated to evaluate the stabilities of (H2) n@C70 ( n = 1, 2, 3). The results show that (H2)2@C70 is more stable than H2@C70. The interaction energy slowly changes in a large temperature range, so temperature has little effect on the stability of the system. For H2@C70 and (H2)2@C70, the interaction energies keep negative; however, when three H2 molecules are in the cage, the interaction energy rapidly increases to a positive value. This implies that at most two H2 molecules can be trapped by C70. With an increase of temperature, the peak of the spatial distribution gradually shifts away from the center of the cage, but the maximum distance from the center of H2 molecule to the cage center is much smaller than the average radius of C70.

PACS: 81.05.ub; 05.10.Ln; 65.80.–g; 68.60.Dv
Keyword: endohedral fullerene complexes; path integral Monte Carlo method; interaction energy; vibrationally averaged spatial distribution
1. Introduction

Endohedral fullerene complex, with small atoms or molecules confined inside an empty fullerene cage, has attracted increasing attention. Because of the interaction between the host fullerene cage and the guest atoms, endohedral fullerene complex not only has the properties of the host cage but it also has the properties of the guests, [1, 2] which makes it widely used in many fields, such as electronics, [3– 5] medicine, [5– 7] environment protection, [8] and renewable energy.[9]

Since La@C82 was macroscopically prepared, [10] significant progress has been made in researching endohedral metallofullerenes. It has been found that a fullerene complex with noble gas atoms can be prepared at high temperature (650 ° C) and high pressure (3000 atm, 1 atm = 1.01325 × 105 Pa).[11, 12] Much theoretical work has also been done to study the stability of this kind of complex.[13– 16] In recent years, a fullerene complex with one or multiple hydrogen molecules has become a popular topic in both experimental and theoretical fields. The amount of work in which various theoretical methods are used has been done with C60 to study the maximum number of H2 molecules that can be trapped by the cage. Turker and Erkoc[17] reported that 24 hydrogen molecules could be inserted into C60 from semiempirical Austin Model 1 (AM1) calculations. Moreover, Ren et al.[18] reported that C60 could encapsulate up to 25 hydrogen molecules on the basis of parametric method 3 (PM3) combined with density-functional theory (DFT). However, the methods they used were considered to be defective and their results were thought to be unreliable.[19, 20] Tatiana Korona et al.[21] used the density functional theory combined with the symmetry adapted perturbation theory (DFT-SAPT) and found that only one H2molecule could be stabilized inside C60. This result is consistent with the fact that H2@C60 has been prepared but not (H2)2@C60.

Recent syntheses of endohedral complexes of C70 with one or two hydrogen molecules have sparked the interest of researchers who wish to study the stability of one or multiple H2 molecules encapsulated into C70 and to predict the maximum number of H2 that can be trapped by C70. Some quantum mechanical methods, such as DFT, second-order Mø ller– Plesset theory (MP2), spin-component scaled MP2 (SCS-MP2), diffusion Monte Carlo (DMC) have been used to evaluate the stabilities of H2@C70 and (H2)2@C70 and they found that both H2@C70 and (H2)2@C70 are energetically stable.[22– 24] Sebastianelli et al.[24] calculated the vibration properties of one or two H2 molecules in a C70 cage. However, their evaluation of the stability and the study of the thermal properties were conducted under the condition of temperature T = 0. Therefore their study cannot reflect the effect of temperature on the properties of the system. Since temperature is a parameter of the density matrix, the path integral Monte Carlo (PIMC) method is an accurate tool that can be used to compute quantum many-body properties at finite temperatures.[25– 27] In this paper we employ the PIMC method to calculate the thermal properties of (H2)n@C70 (n = 1, 2, 3).

The rest of this paper is organized as follows. In Section 2, we briefly introduce part of the PIMC theory relating to our study and the details of our simulation. In Section 3, we give our results and discussion, analyzing the temperature-dependent interaction energies of (H2)n@C70 (n = 1, 2, 3) obtained from PIMC calculations and we will study the movement of H2 molecules in the C70 cage through one-dimensional (1D) and three-dimensional (3D) probability distribution functions (PDFs). Our conclusions are given in Section 4.

2. Method

In the PIMC method, all observations can be expressed as statistics relating to the sampled paths. In the coordinate image, when a system is in a state of thermal equilibrium, the value of an operator O can be written as

where the partition function is z = ∫ drρ (R, R; β ), with ρ (R, R′ ; β ) denoting the density matrix.

In quantum mechanics, the density matrix is a basic physical quantity. Theoretically, all of the equilibrium properties of a quantum system can be obtained from the density matrix, which can be written as[25]

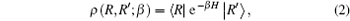
where β is the inverse temperature and β = 1/KBT, with KB being the Boltzmann constant and T being the temperature, and H is the Hamiltonian. Since the density matrix of the system is not just about the Hamiltonian but also about the system temperature, the PIMC method can calculate the properties of systems under different temperatures.

The above expression can be expanded into a path of M steps in imaginary time, each step of duration τ = β /M is expressed as[25, 27]

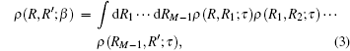
where {R, R1, R2, … , RM− 1, R′ } denotes the path in position space. Hence the density matrix at temperature T can be expressed as the density matrix at higher temperature MT. When M is a limited integer, the path is discrete; however, when M → ∞ , the path is continuous.

Because multiple H2 molecules are involved in our system, the exchange between these identical particles must be taken into account. Since H2 molecules are bosons, we only consider the exchange occurring in a Bose system. For identical particles, the density matrix is[24]

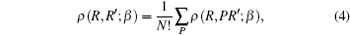
where P is a permutation, N is the number of the particles, and (P1, P2, … , PN) is an all-permutations of (1, 2, … , N). The system with N identical particles has N! different permutations.

PDFs are used to describe the vibrationally averaged spatial distribution of H2 molecules, [28] which are defined as

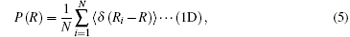
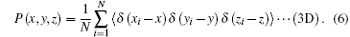
Equation (5) is a 1D probability function and equation (6) is a 3D probability function, which can be calculated by the PIMC method, (x, y, z) are the Cartesian coordinates of the H2 molecule, 〈 · · · 〉 denotes the configurational average over the sampled paths, and R is the distance from the cage center to the center of caged H2 molecule. The PDFs are different under different temperatures and, when temperature is considered, the PDFs can be written as P(R; T) and P(x, y, z; T).

Because of the encapsulation a small number of H2 molecules can cause negligible distortions to the fullerene geometries, [29] we treat fullerene C70 as being rigid. In the case of hydrogen molecules, we treat them as spatial particles, which is proven to be accurate by calculating the properties of confined H2 in isotropic environments.[30, 31] In our study, the C70 cage is considered to be fixed, our study only involves the movement of H2 molecules. The (H2)n– C70 (n = 1, 2, 3) interaction is described by the sum of the pair potentials between H2 molecule and each of the 70 carbon atoms, as well as the intermolecular pair potentials between each H2 molecules when n > 1. For H2– C pair potential, we use 6– 12 Lennard-Jones (LJ) potential (6– 12 LJ potential).[32] In the case of H2– H2 pair potential, Silver– Goldman potential (SG potential)[33] is employed. In our program, we use linear grids and the number of grids is 250. For carbon atoms, which are considered to be classical particles, the quantumness parameter λ is taken as 0 K· Å 2. For H2 molecules, λ is taken to be 12.127 K· Å 2. The number of partial waves is set to be 100. n-square, which is the total number of squarings to reach the lowest temperature and is set to be 14. We use the bisection method to sample the paths and ensure that the acceptance for the moves reaches about 50%.

3. Results and discussion
3.1. Interaction energies

In this paper, temperature-dependent interaction energies are used to evaluate the stabilization of the endohedral fullerene complexes (H2)n@C70 (n = 1, 2, 3), which are shown in Fig. 1. Table 1 shows our results at 1 K, which are compared with the results from three other quantum-mechanical calculations under the condition of temperature T = 0.

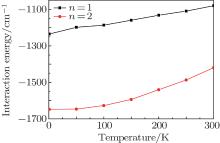Fig. 1. Plots of interaction energy versus temperature for (H2)n@C70 (n = 1, 2) system from PIMC calculation. The units for temperature and energy are Kelvin and cm− 1 respectively.
Table 1. Comparison of the interaction energy at 1 K calculated in this work with those from three other quantum-mechanical methods (T = 0). All energies are in cm− 1.

At 1 K, the interaction energies of H2@C70, (H2)2@C70, and (H2)3@C70 calculated by PIMC method are − 1234.53 cm− 1, − 1648.07 cm− 1, and 2670.75 cm− 1, respectively. This result is closest to the values obtained by DMC calculation (T = 0). The maximum difference between them is about 11%. The reason for this difference is that the interaction potentials used in DMC calculation and in this work are different. In this work, we use the SG potential to describe the interaction of H2– H2. In the DMC method, the H2– H2 potential is described by the ab initio four-dimensional (4D) intermolecular potential energy surface (PES). For H2– C pair potential, we use 6– 12 LJ potential, which is a standard two-site H2– C pair potential; however, the DMC method uses the three-site H2– C pair potential, which can be used to study the translation– rotation excitations of the system.

Since the interaction energies for one and two H2 molecules caged in C70 are negative, it can be inferred that both H2@C70 and (H2)2@C70 are energetically stable. Furthermore, the interaction energy of (H2)2@C70 is greater than that of H2@C70, about a 34% increase (in absolute value), implying that the former is more stable than the latter. However, when three H2 molecules are encapsulated in C70, the interaction energy rapidly jump to a high positive value (2670.75 cm− 1). The reason why C70 cannot trap three H2 molecules may be that the C70 room is too crowded for three H2 molecules to move and each H2 molecule will be repelled by the other two H2 molecules.

From Fig. 1 we can see that for each of the complexes (H2)n@C70 (n = 1, 2), the interaction energy increases gradually with the increase of temperature, which happens because of a stronger vibration of H2 molecules at a higher temperature. Meanwhile, in a wide temperature range (from 1 K to 300 K), the interaction energy remains negative for H2@C70 and (H2)2@C70, so temperature has little effect on interaction energy. The result calculated by the PIMC method shows that C70 can trap two H2 molecules at most and is in agreement with the syntheses of H2@C70 and (H2)2@C70 but not (H2)3@C70.

3.2. 3D PDF P(x, y, z)

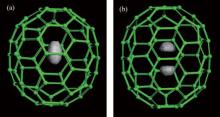
The 1D and 3D PDFs are calculated to analyze the spatial distributions of one and two H2 molecules in the C70 cage. Figure 2 displays the 3D PDF, P(x, y, z), under 1 K from the PIMC calculations for (H2)n@C70 (n = 1, 2). This figure can vividly show the spatial distribution of H2 molecules in C70. For n = 1, the P(x, y, z) is egg-shaped and occupies the center of the cage, meanwhile it extends along the C5 axis of C70. For n = 2, the P(x, y, z) consisting of two distinct lobes, which are symmetrically distributed on both sides of the cage center, that the C5 axis of C70 passes through. What is noteworthy is that the bottoms of the lobes are flat, proving that the two H2 molecules are mutually exclusive.

Fig. 2. 3D probability distribution P(x, y, z) for (a) one H2 in C70 and (b) two H2 in C70, from the PIMC calculations.
3.3. 1D PDF P(R)

To obtain more detailed information about the movement of the H2 molecule inside the cage, the 1D PDF is calculated. Figure 3 shows the 1D PDF, P(R), for (H2)n@C70 (n = 1, 2) under different temperatures (1 K, 50 K, 100 K, 200 K, and 300 K). Where R is the distance between the center of the hydrogen molecule and the cage center. Figure 3(a) shows that for n = 1, the H2 molecule is not fixed in the cage center but has a probabilistic distribution around the cage center. For n = 2, the distance from either of the two H2 molecules to the cage center is equal, which may be due to the fact that the two H2 molecules are identical and the intermolecular interaction can have an equal effect on them. Figure 3(b) displays the temperature-dependent spatial distributions for two H2 molecules in C70, from which we can see when two H2 molecules are confined in the cage, their distributions are also probabilistic within a small region. For both n = 1 and n = 2, each P(R) is enlarged and the peak gradually shifts away from the cage center with the increase of temperature. This phenomenon shows that the thermal vibrations of the caged H2 molecules are enhanced at a higher temperature. However, in a wide temperature range, R remains much shorter than the average radius of caged C70. Meanwhile, as the temperature increases, the change of P(R) for n = 2 is smaller than that for n = 1, which complementally reflects that (H2)2@C70 is more stable than H2@C70.

Fig. 3. 1D probability distribution P(R) for (a) one H2 molecule and (b) two H2 molecules in C70, from the PIMC calculations.
Fig. 4. Plots of 1D probability distribution P(R) of one or two H2 molecules in C70 from the PIMC calculations at a temperature 300 K.

To intuitively compare the spatial distribution differences, the 1D PDF P(R)s for n = 1 and n = 2 under 300 K are plotted together in Fig. 4. For n = 1, H2 moves within a region with a radius of 2.5 Bohr and the peak appears near 1.0 Bohr. While for n = 2, the distribution radius of H2 molecule varies between 1.0 Bohr and 3.0 Bohr and the peak appears near 2.1 Bohr. Obviously, compared with one H2 molecule, two H2 have less room to move, so their amplitudes diminish. Furthermore, for n = 2, P(R) = 0 when R < 1.0 Bohr. This is caused by the intermolecular interaction, which stays away from the cage center.

4. Conclusions

A PIMC method is used to study the thermal properties of H2 molecules inside the C70 cage. The temperature-dependent interaction energies and spatial distributions of (H2)n@C70 (n = 1, 2, 3) are calculated. From 1 K to 300 K, the interaction energies are negative for one or two H2 molecules caged in C70, while for (H2)3@C70, the interaction energy is positive. Therefore, the C70 cage can trap two H2 molecules at most. Meanwhile the result shows that (H2)2@C70 is more stable in energy than H2@C70. In both H2@C70 and (H2)2@C70 systems, the spatial distributions show that H2 molecule stays further away from the cage center when temperature increases. Meanwhile, this change is slow and the distance from H2 molecule to the cage center is much shorter than the average radius of the C70 cage. In this paper, for the interaction between H2 molecule and the C70 cage, we use LJ potential. For further study, a more accurate potential should be used to analyze the rotation of the H2 molecules in the cage. Moreover, other properties, such as the spectroscopic properties of (H2)n@C70 (n = 1, 2, 3) under different ambient conditions, can be studied to find more applications of the systems. Because PIMC is an accurate tool to study quantum many-body properties, it can be used to study other fullerene complexes, such as boron fullerene complexes and boron– nitrogen fullerene complexes.

Reference
1 Stevenson S, Rice G, Glass T, Harich K, Cromer F, Jordan M R, Craft J, Hadju E, Bible R, Maitra K, Fishe A J, Balch A L and Dorn H C 1999 Nature 401 55 DOI:10.1038/43415 [Cited within:1]
2 Wang C R, Kai T, Tomiyama T, Yoshida T, Kobayashi Y, Nishibori E, Takata M, Sakata M and Shinohara H 2001 Angew. Chem. Int. Ed. 40 397 DOI:10.1002/(ISSN)1521-3773 [Cited within:1]
3 Kobayashi S, Mori S, Iida S, Ando H, Takenobu T, Taguchi Y, Fujiwara A, Taninaka A, Shinohara H and Yoshihiro I 2003 J. Am. Chem. Soc. 125 8116 DOI:10.1021/ja034944a [Cited within:1]
4 Shibata K, Kubozono Y, Kanbara T, Hosokawa T, Fujiwara A, Ito Y and Shinohara H 2004 Appl. Phys. Lett. 84 2572 DOI:10.1063/1.1695193 [Cited within:1]
5 Yasutake Y, Shi Z J, Okazaki T, Shinohara H and Majima Y 2005 Nano Lett. 5 1057 DOI:10.1021/nl050490z [Cited within:2]
6 Cagle D W, Kennel S J, Mirzadeh S, Alford J M and Wilson L J 1999 Proc. Natl. Acad. Sci. USA 96 5182 DOI:10.1073/pnas.96.9.5182 [Cited within:1]
7 Li J, Sun H and Dai Y D 2010 Chin. Phys. Lett. 27 038104 DOI:10.1088/0256-307X/27/3/038104 [Cited within:1]
8 Mauter M S and Elimelech M 2008 Environ. Sci. Technol. 42 5843 DOI:10.1021/es8006904 [Cited within:1]
9 Staden R S and Lal B 2006 Anal. Lett. 39 1311 DOI:10.1080/00032710600666396 [Cited within:1]
10 Chai Y, Cuo T, Jin C M, Haufler R E, Chibante L P F, Fure J, Wang L H, Alford J M and Smalley R E 1991 J. Phys. Chem. 95 7564 DOI:10.1021/j100173a002 [Cited within:1]
11 Saunders M, Jiménez-Vázquez H A and Cross R J 1994 J. Am. Chem. Soc. 116 2193 DOI:10.1021/ja00084a089 [Cited within:1]
12 Peres T, Cao B P, Cui W D, Khong A, Cross R J, Saunders M and Lifshitz C 2001 Int. J. Mass Spectrom. 210 241 [Cited within:1]
13 Peng C, Zhang H and Cheng X L 2013 Chin. Phys. Lett. 30 116501 DOI:10.1088/0256-307X/30/11/116501 [Cited within:1]
14 Slanina Z, Pulay P and Nagase S 2006 J. Chem. Theor. Comput. 2 782 DOI:10.1021/ct0503320 [Cited within:1]
15 Pang L and Brisse F 1993 J. Phys. Chem. 97 8562 DOI:10.1021/j100135a005 [Cited within:1]
16 Fernández I, Solá M and Bickelhaupt F M 2014 J. Chem. Theor. Comput. 10 3863 DOI:10.1021/ct500444z [Cited within:1]
17 Turker L and Erkoc S 2006 Chem. Phys. Lett. 426 222 DOI:10.1016/j.cplett.2006.05.053 [Cited within:1]
18 Ren Y X, Ng T Y and Liew K M 2006 Carbon 44 397 DOI:10.1016/j.carbon.2005.09.009 [Cited within:1]
19 Dolgonos G 2005 J. Mol. Struct. Theochem. 732 239 DOI:10.1016/j.theochem.2005.02.017 [Cited within:1]
20 Dodziuk H 2006 Chem. Phys. Lett. 426 224 DOI:10.1016/j.cplett.2006.05.054 [Cited within:1]
21 Korona T, Hesselmann A and Dodziuk H 2009 J. Chem. Theor. Comput. 5 1585 DOI:10.1021/ct900108f [Cited within:1]
22 Murata M, Maeda S, Morinaka Y, Murata Y and Komatsu K 2008 J. Am. Chem. Soc. 130 15800 DOI:10.1021/ja8076846 [Cited within:1]
23 Kruse H and Grimme S 2009 J. Phys. Chem. C 113 17006 DOI:10.1021/jp904542k [Cited within:1]
24 Sebastianelli F, Xu M Z, Bačić Z, Lawler R and Turro N J 2010 J. Am. Chem. Soc. 132 9826 DOI:10.1021/ja103062g [Cited within:3]
25 Ceperley D M 1995 Rev. Mod. Phys. 67 279 DOI:10.1103/RevModPhys.67.279 [Cited within:3]
26 Zhao X W Cheng X L Zhang H 2010 Acta Phys. Sin. 59 482 (in Chinese) DOI:10.1038/aps.2012.120 [Cited within:1]
27 Wagner M and Ceperley D M 1994 J. Low Temp. Phys. 94 185 [Cited within:2]
28 Sebastianelli F, Xu M Z and Bačić Z 2008 J. Chem. Phys. 129 244706 DOI:10.1063/1.3049781 [Cited within:1]
29 Slanina Z, Pulay P and Nagase S 2006 J. Chem. Theor. Comput. 2 782 DOI:10.1021/ct0503320 [Cited within:1]
30 Garberoglio G, DeKlavon M M and Johnson J K 2006 J. Phys. Chem. B 110 1733 DOI:10.1021/jp054511p [Cited within:1]
31 Garberoglio G and Johnson J K 2010 ACS Nano 4 1703 DOI:10.1021/nn901592x [Cited within:1]
32 Roussel T, Bichara C, Gubbins K E and Pellenq R J M 2009 J. Chem. Phys. 130 174717 DOI:10.1063/1.3122382 [Cited within:]
33 Silvera I F and Goldman V V 1978 J. Chem. Phys. 69 4209 DOI:10.1063/1.437103 [Cited within:1]