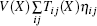†Corresponding author. E-mail: scu kxy@163.com
*Project supported by the National Natural Science Foundation of China (Grant No. 11274235), the Young Scientist Fund of the National Natural Science Foundation of China (Grant No. 11104190), and the Doctoral Education Fund of Education Ministry of China (Grant Nos. 20100181110086 and 20110181120112).
The energy term corresponding to the first order of the strain in Taylor series expansion of the energy with respect to strain is always ignored when high-pressure elastic constants are calculated. Whether the modus operandi would affect the results of the high-pressure elastic constants is still unsolved. To clarify this query, we calculate the high-pressure elastic constants of tantalum and rhenium when the energy term mentioned above is considered and neglected, respectively. Results show that the neglect of the energy term corresponding to the first order of the strain indeed would influence the veracity of the high-pressure elastic constants, and this influence becomes larger with pressure increasing. Therefore, the energy term corresponding to the first-order of the strain should be considered when the high-pressure elastic constants are calculated.
Accurate calculations of the high-pressure elastic constants based on the first-principles are crucial to predicting the high-pressure behaviors of the elastic properties and providing fundamental understanding of the properties of interatomic forces, mechanical stabilities, [1] and phase transition mechanisms of materials under high pressures.[2, 3]
Among the existing first-principle approaches[4– 35] to calculating the high-pressure elastic constants, total energy approach[4– 12, 18– 22] is the most frequently used method. The kernel of this method is to expand the energy of the deformed system into Taylor series with respect to the strain[36] as shown below
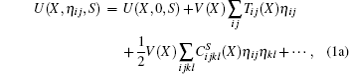 |
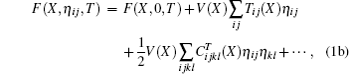 |
where X is the reference state corresponding to the equilibrium state at a certain pressure, V denotes the volume of the system in X state, U and F are the internal energy and Helmholtz free energy respectively, S and T refer to the adiabatic and isothermal processes respectively. Subscript η ij represents the element of the strain tensor, Tij (X) is the component of the stress tensor exerted on X state,

and
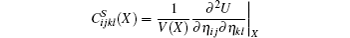
are the second-order elastic constants. Since the stress acting on the reference state X is nonzero, the energy term 
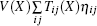
To clarify this puzzling issue, we take the cubic tantalum (Ta) and hexagonal rhenium (Re), for example, and calculate their high-pressure elastic constants when the term of 
Structural optimizations and total energy calculations at 0 K are performed by using the Vienna ab initio simulation package (VASP).[50, 51] The Perdew– Burke– Ernzerhof (PBE) version[52] of the general gradient approximation (GGA) is used for the electron exchange– correlation functional. Electrons of 5p66s25d3 for Ta and 5p66s25d5 for Re are treated as valence configurations. The interaction between the valence electrons and the remaining core electrons is described by the frozen core projector-augmented wave (PAW) method.[53] Energy convergence (1 mRy per atom) tests are performed to determine the cutoff energy and the number of k-points in whole pressure range for both metals, and the reasonable cutoff energy (400 eV for Ta and 450 eV for Re) and rational k-points (18 × 18 × 18 for Ta and 14 × 14 × 10 for Re) are ascertained. Afterwards, the total energy of undeformed unit cell is calculated in a volume range of 0.45 V0expt– 1.1 V0expt, where V0expt is the experimental equilibrium volume at zero pressure. Then the equation of states at 0 K for both metals are determined according to the fourth-order Brich– Murnaghan equation 
To determine the three elastic constants of cubic Ta, the following formula is first used:

and its detailed derivations are given in Appendix A.
For calculating C11 and C12, we adopt the volume conserving deformation gradient matrix, i.e.,

which is obtained from the shear deformation of the (110) plane in the 

and

where E(0) represents the energy of the undeformed unit cell, V denotes the corresponding volume, Cij and C̄ ij represents the elastic constants obtained respectively when the 

In addition, the volume conserving deformation gradient matrix (5), which represents the deformation of the (100) plane shear in the [010] direction, is used to calculate the C44 (C̄ 44).
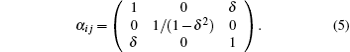
The corresponding energy expressions are
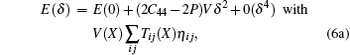
and

With the aid of formulas (4) and (6), we can obtain C11 − C12(C̄ 11 − C̄ 12) and C44 (C̄ 44) of Re in the same way as that in the case of Ta. To calculate C11 (C̄ 11), C12 (C̄ 12), C13 (C̄ 13), and C33 (C̄ 33) respectively, we first employ the following expression:

where


Detailed derivations of the formula (7) are presented in Appendix A. In addition, the volume dependence of the equilibrium c/a rate is related to the difference in linear compressibility between along the a and along the c axes, which is described by the dimensionless quantity R
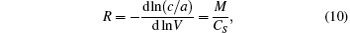
where

The detailed deductions of Eq. (10) are shown in Appendix B. It should be pointed out that formulas (8), (9), and (11) can also be expressed by C̄ ij in the same way.
To calculate the CS appearing in formulas (7) and (10), the volume-conserving deformation matrix (12) is used, i.e.,

The corresponding expressions of the energy are

and
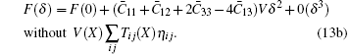
Then we can respectively obtain the C11 (C̄ 11), C12 (C̄ 12), C13 (C̄ 13), and C33 (C̄ 33) by solving Eqs. (4), (7), (10), and (13).
To verify the accuracy of the present calculations, we list the calculated lattice parameters, the values of equilibrium volume V0, bulk modulus B0, and their pressure derivative 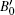
Table 1. Calculated values of equilibrium lattice parameter (in unit Å ), atomic volume V0 (in unit Å 3), bulk modulus B0 (in unit GPa), and their pressure derivative  |
From Table 1, we can clearly see that the calculated lattice parameters of Ta and Re are in fair agreement (within 0.5%) with the experimental data.[45– 50] And the equilibrium volumes, bulk modulus B0 and their pressure derivatives 
Having seen that the calculations of the present work are reliable, we now turn to the results of the high-pressure elastic constants.
The relationships between the pressure and elastic constants, obtained respectively when the energy term 

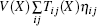

Through the calculations of the high-pressure elastic constants of the cubic Ta and hexagonal Re when the energy term corresponding to the first-order of the strain is considered and ignored respectively, we find the energy term corresponding to the first-order of the strain indeed will affect the calculated results of the high-pressure elastic constants and such an influence grows larger with pressure increasing. Therefore, the energy term corresponding to the first-order of the strain in the Taylor series expansion of the total energy with respect to the strain should not be ignored when the high-pressure elastic constants are calculated.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|
| 55 |
|
| 56 |
|
| 57 |
|
| 58 |
|
| 59 |
|
| 60 |
|
| 61 |
|