†Corresponding author. E-mail: wudeyu2585@163.com
‡Corresponding author. E-mail: alatanca@imu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11101200 and 11371185) and the Natural Science Foundation of Inner Mongolia Autonomous Region, China (Grant No. 2013ZD01).
In this paper, the ascent of 2× 2 infinite dimensional Hamiltonian operators and a class of 4× 4 infinite dimensional Hamiltonian operators are studied, and the conditions under which the ascent of 2× 2 infinite dimensional Hamiltonian operator is 1 and the ascent of a class of 4× 4 infinite dimensional Hamiltonian operators that arises in study of elasticity is 2 are obtained. Concrete examples are given to illustrate the effectiveness of criterions.
The traditional method of separation of variable (also called Fourier method) is an effective method for solving partial differential equations that can be transformed into the Strum– Liouville problem after separating variables, such as vibrating string equation and harmonic equation. The theoretical basis for Fourier method is completeness of eigenvectors system of self-adjoint operator, so the completeness of eigenvectors system is paid considerable attention.[1– 5] We recall that the eigenvector system {eα }α ∈ A of a linear operator T is called complete in space X, if 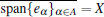
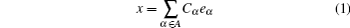
holds, which may be finite or infinite, convergence in norm (see Tehorem II.6 in Ref. [6]), then {eα }α ∈ A is said to be complete in space X.
However, a great number of applied problems, like the second-order elliptic equation, cannot be reduced to the Strum– Liouville problem, as a consequence, the Fourier method fails to work. In order to overcome this problem, Zhong[7] using the simulation theory between structural mechanics and optimal control introduced Hamiltonian systems into elasticity and proposed the sympletic Fourier method based on Hamiltonian systems, and which generalizes the traditional method of separation of variables and possesses far-reaching significance. It is worth noting that corresponding operator of a Hamiltonian system is called infinite dimensional Hamiltonian operator and it has the following block representation:
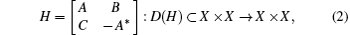
where A is densely defined closed linear operator, B, C are self-adjoint operators (see Refs. [8] and [9] and references therein). An infinite dimensional Hamiltonian operator is generally non-self-adjoint and perhaps has generalized eigenvectors, but its root vectors system (i.e., the eigenvector and the generalized eigenvector) is symplectic-orthogonal, and thus the completeness of symplectic-orthogonal root vectors system is the theoretical basis for symplectic Fourier method. The completeness of symplectic orthogonal eigenvectors system has been considered in Refs. [3], [10], and [11]. But the completeness of the root vectors system has not been completely understood, especially, the existence problem of generalized eigenvectors is one of the urgent things in spectral theory of infinite dimensional Hamiltonian operator. Therefore, the main aim of this note is to study the ascent of 2× 2 infinite dimensional Hamiltonian operators and a class of 4× 4 infinite dimensional Hamiltonian operators and obtain the sufficient conditions under which the ascent of the infinite dimensional Hamiltonian operator is 1 or 2.
As we know, the existence of generalized eigenvectors has to do with the ascent of linear operator. We recall that the ascent (see for example Taylor[12]) of T at λ (denoted by Pλ (T)) is the smallest positive integer k such that

If there exists v ≠ 0 such that (T – λ )v = u, where u ∈ N(T – λ ), then v is called generalized eigenvector of the first order, and which implies that the ascent of T at λ is lager than 1 (i.e., Pλ (T) ≥ 2). Similarly, one may define the generalized eigenvector whose order is k. The system of eigenvectors and root vectors (i.e., eigenvectors and generalized eigenvectors) are overlapped when Pλ (T) = 1 for all λ ∈ σ p(T).
Throughout this paper, X always denotes the separable infinite dimensional complex Hilbert space and consider the orthogonal direct sum X × X which is a Hilbert space whose inner product is also denoted by (· , · ). The symbols 
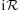
We start with the following lemma.
Lemma 1 Let T be a densely defined closed operator in a Hilbert space X, and for any u ∈ N(T – λ ) there exists v ∈ N(T* –
Proof Suppose Pλ (T) = k + 1, then there exists u0 ∈ X such that
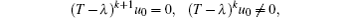
and which implies (T − λ )ku0 ∈ N(T − λ ). By given condition, there exists v ∈ N(T* −
Remark 1 For any λ ∈ σ p(T), if Pλ (T) = 1 then we can see that the system of eigenvector and root vectors are overlapped, i.e., the generalized eigenvector does not appear, in this case we need only to consider the completeness of eigenvectors system. On the contrary, if Pλ (T) ≥ 2, then there exist generalized eigenvectors and we may consider the completeness of root vectors system, and which implies that the symplectic Fourier method generalizes the traditional Fourier method, since the self-adjoint operator has no generalized eigenvectors. Therefore, it is of interest to find conditions under which the ascent of T at λ is 1, 2 or others.
Theorem 1 Let 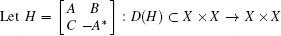
(i) If B− 1A is a symmetric operator (i.e., (B− 1Ax, x)∈ R, ∀ x ∈ D(A)). Then for any 0 ≠ λ ∈ σ p(H) we have Pλ (H) = 1.
(ii) If C + (A* + λ )B− 1(A − λ ) is surjective, λ ∈ σ p(H). Then Pλ (H) ≥ 2.
Proof
(P-1) Let u = [f g]T ∈ N(H − λ ), then in view of
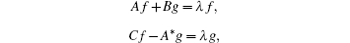
we obtain
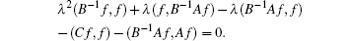
Since (B− 1Af, f) ∈ R, so we have λ (f, B− 1Af) − λ (B− 1Af, f) = 0 and
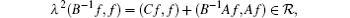
and thus 
If 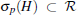
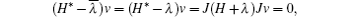
and
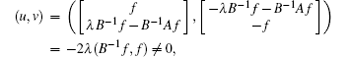
hence by Lemma 1, Pλ (H) = 1.
If 
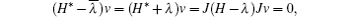
and

hence by Lemma 1, we also have Pλ (H) = 1.
P-2 Let u = [f g]T ∈ N(H − λ ), then g = λ B− 1f − B− 1Af. Since operator C + (A* + λ )B− 1(A − λ ) is surjective, so there exists v1 ∈ D(A) ∩ D(C) such that
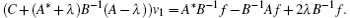
Therefore, taking v = [v1B− 1f − B− 1(A − λ )v1]T then we have
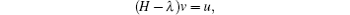
and which implies Pλ (H) ≥ 2. The proof is complete.
Remark 2 When B− 1A is symmetric and 0 ∈ σ p(H), then the ascent of H at λ = 0 is larger than 1. In fact, let u = [f g]T ∈ N(H), and taking v = [f − B− 1Af + B− 1f]T, then in view of D(B) ⊆ D(A* ), g = − B− 1Af = A* B− 1f, and Cf + A* B− 1Af = 0 we have v ∈ D(H), v ≠ 0, and

which implies that the ascent of H at 0 is larger than 1 (i.e., exist generalized eigenvectors).
Remark 3 When D(C) ⊂ D(A), C is positive and C− 1A* is a symmetric operator then we also obtain a similar conclusion.
Next we shall give an example to illustrate the effectiveness of Theorem 1.
Example 1 Consider the following partial differential equation

and transform it into Hamiltonian system then we obtain the following Hamiltonian regular equation
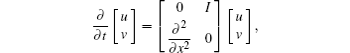
where ∂ v/∂ t = ∂ 2u/∂ x2. Let X = L2[0, 1], then we obtain the following Hamiltonian operator

where D(C) = {x ∈ X : x′ absolutely continuous, x′ , x″ ∈ X, x(0) = x(1) = 0}. It is easy to check that 0 ∈ ρ (B), D(B) ⊂ D(A* ) and B− 1A = 0 is symmetric, so by Theorem 1, we have Pλ (H) = 1 for any 0 ≠ λ ∈ σ p(H) (i.e., the operator H has no generalized eigenvectors).
On the other hand, through direct calculation we can obtain that the eigenvector system and the root vectors system of the infinite dimensional Hamiltonian operator H are overlapped and are equal to

corresponding eigenvalues are λ k = kπ , k = ± 1, ± 2, … , which tallies with the above theoretical result.
When Pλ (H) ≥ 2, the operator exists generalized eigenvectors, hence one may consider the completeness of the root vectors system (i.e. the eigenvector and the generalized eigenvector). The main aim of this section is to obtain the sufficient conditions under which the ascent of a class of infinite dimensional Hamiltonian operator is 2 (i.e., except eigenvectors, the infinite dimensional Hamiltonian operator only has the first-order generalized eigenvectors). But, for general infinite dimensional Hamiltonian operators, it is not so easy to obtain the conditions of the ascent being 2, and because lots of infinite dimensional Hamiltonian operators which appear in the study of elasticity are of the form
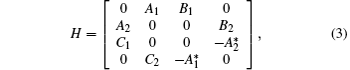
see the following examples.
Example 2 The basic equation of a plate strip is as follows:[13]
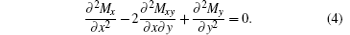
Let
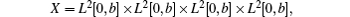
then the corresponding infinite dimensional Hamiltonian operator of the system (4) is

where D > 0 and
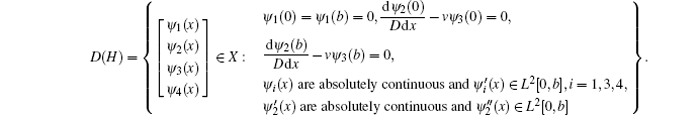
Example 3[14] The free vibration of rectangular thin plates with two opposite edges simply supported is given by
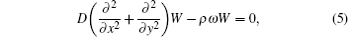
where W(x, y) is the vibration model, ρ is the mass density, D is the bending stiffness, and ω is the natural frequency. The boundary conditions for simply supported edges y = 0 and y = 1 are
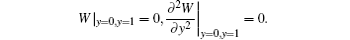
Let X = L2[0, 1] × L2[0, 1] × L2[0, 1] × L2[0, 1], then the corresponding infinite dimensional Hamiltonian operator of system (5) is

where
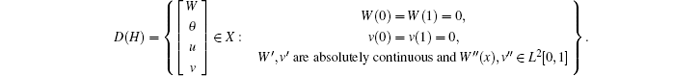
Consequently, in this section the ascent of infinite dimensional Hamiltonian operators of form (3) is considered, and the sufficient condition of Pλ (H) = 2 is given.
Theorem 2 Let
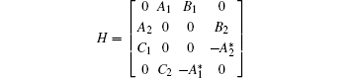
be infinite dimensional Hamiltonian operator with Bi > M, Ci ≥ 0, 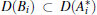
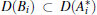
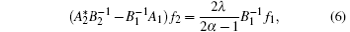

hold then the accent of H at λ is 2.
Proof Suppose 0 ≠ λ ∈ σ p(H) and U = [f1f2g1g2] be a corresponding eigenvector. In view of (H − λ )U = 0 and the invertibility of Bi, i = 1, 2, we have

and thus
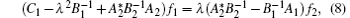
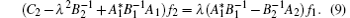
Taking
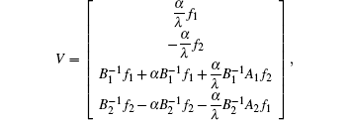
then on account of Eqs. (6)– (9) we have

that it to say, the accent of λ satisfies Pλ (H) ≥ 2.
On the other hand, taking

and
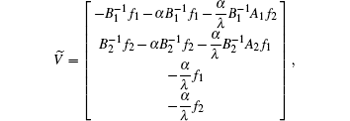
then on account of Eqs. (6) and (7) and H* | D(JHJ) = JHJ, we have

and
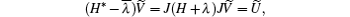
that it to say, Ṽ ∈ N((H* −
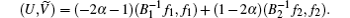
Since α 2 > 1/4, so (− 2α − 1)(1 − 2α ) > 0, as a consequence (U, Ṽ ) ≠ 0 and by Lemma 1 we have Pλ (H) ≤ 2, and thus Pλ (H) = 2.
When 0 ∈ σ p(H), let U = [f1f2g1g2]T be a corresponding eigenvector, taking
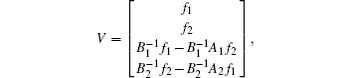
then we have
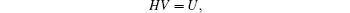
that it to say, the accent of λ = 0 satisfies P0(H) ≥ 2.
On the other hand, taking
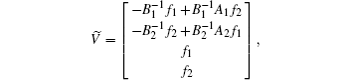
then we have
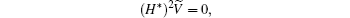
and
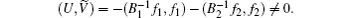
By Lemma 1 we have P0(H) ≤ 2, and thus P0(H) = 2.
Remark 4 In Example 2, it is easy to check that Bi > M, Ci ≥ 0, 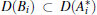
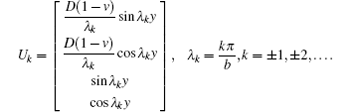
Taking α = 3 + v/2(v − 1), then α 2 > 1/4 (since the Poisson ratio v satisfies 0 ≤ v ≤ 0.5) and
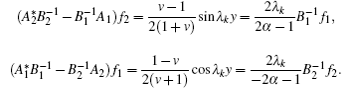
By Theorem 2, the accent of λ ∈ σ p(H) is 2.
On the other hand, through direct calculation we can see (see also Ref. [13]) that the operator H has the first-order generalized eigenvectors (i.e., Pλ k(H) = 2)

and which tallies with the above theoretical result.
Fourier method is based on the completeness of eigenfunctions system with self-adjoint operator. Since the ascent of the self-adjoint operator is 1, so the eigenvector system and the root vector system are overlapped. However, the symplectic Fourier method based on infinite dimensional Hamiltonian operator whose ascent is maybe lager than 1, therefore, it is of interest to find conditions under which the ascent of infinite dimensional Hamiltonian operator is 1 or 2. Hence, in this paper we obtain the conditions under which the ascent of 2× 2 infinite dimensional Hamiltonian operator is 1 and the ascent of a class of 4× 4 infinite dimensional Hamiltonian operators is 2. Our results are helpful to provide theoretical basis for symplectic Fourier method.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|


