Electric dipole moment function and line intensities for the ground state of carbon monxide<xref ref-type="fn" rid="cpb142925fn1">*</xref>

Cite this Article

Chen Hua-Jun, Wu Jie, Liu Hao, Cheng Xin-Lu†. Electric dipole moment function and line intensities for the ground state of carbon monxide* . Chinese Physics B, 24(8): 083102 Copy to clipboard

Permissions

Electric dipole moment function and line intensities for the ground state of carbon monxide*

Chen Hua-Jun^a), Wu Jie^b), Liu Hao^b), Cheng Xin-Lu†^a)

a)Institute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China

b)Science and Technology on Optical Radiation Laboratory, Beijing 100854, China

^†Corresponding author. E-mail: chengxl@scu.edu.cn

^*Project supported by the National Natural Science Foundation of China (Grant Nos. 11374217 and 11474207).

Abstract

An accurate electric dipole moment function (EDMF) is obtained for the carbon monoxide (CO) molecule (X¹Σ⁺) by fitting the experimental rovibrational transitional moments. Additionally, an accurate ab initio EDMF is found using the highly accurate, multi-reference averaged coupled-pair functional (ACPF) approach with the basis set, aug-cc-pV6Z, and a finite-field with ±0.005 a.u. (The unit a.u. is the abbreviation of atomic unit). This ab initio EDMF is very consistent with the fitted ones. The vibrational transition matrix moments and the Herman–Wallis factors, calculated with the Rydberg–Klein–Rees (RKR) potential and the fitted and ab initio EDMFs, are compared with experimental measurements. The consistency of these line intensities with the high-resolution transmission (HITRAN) molecular database demonstrates the improved accuracy of the fitted and ab initio EDMFs derived in this work.

PACS: 31.15.A–; 31.50.Bc; 33.20.Ea; 33.20.Vq

Keyword: electric dipole moment; vibrational transition matrix moments; Herman–Wallis factors; line intensities

Show Figures

1. Introduction

Carbon monoxide (CO) is a stable and important diatomic molecule and has been detected in interstellar clouds as well as the Earth’ s atmosphere.^[1] The spectral parameters of CO are included in well-known spectroscopic databases such as the high-resolution transmission (HITRAN) molecular database, ^[2] the high-temperature version of HITRAN called the HITEMP database, ^[3] and others. For CO and other molecules, calculations of line parameters are closely related to their electric dipole moment functions (EDMFs). With the progress of experimental technology, further investigation of the EDMF for CO (X¹Σ ⁺) based on new experimental data is possible.

Several band systems of CO have been observed. Numerous spectral line parameter measurements of CO have been collected for the fundamental band 1– 0, ^{[4– 7]} the first overtone 2– 0, ^{[7– 11]} and the second overtone 3– 0.^{[8, 12– 17]} Many studies in the past decade have focused on the 3– 0 band by using a variety of experimental designs. Chackerian and Valero^[18] measured the absolute rovibrational intensities of the 4– 0 band of carbon monoxide, and more recently Ogilvie et al.^[19] have evaluated the electric dipolar moments based on new experimental measurements of line strengths including the 4– 0 band of ¹²C¹⁶O. Furthermore, Chung et al.^[20] adapted a cavity ringdown spectral technique in the near-infrared region to measure the 5– 0 band for the first time.

Several EDMFs for the ground state of CO have been deduced with various methods based on experimental data with Δ υ ≤ 4.^{[8, 12, 19, 21– 26]} For instance, based on the inversion of experimental intensity information, Chackerian and Tipping^[22] derived a hybrid EDMF in a Padé approximant. It was used to calculate the rovibrational intensities of the ground state CO (X¹Σ ⁺) by Goorvitch et al.^{[27, 28, 29]} In consideration of these pure vibrational matrix elements of the bands υ ′ – 0 with 0 ≤ υ ′ ≤ 5, Chung et al. derived an EDMF in a polynomial form.^[20] A considerable number of quantum chemical calculations of EDMFs for CO have been presented in various papers.^{[19, 30– 37]} However, we find that the vibrational transition matrix elements (or rotationless transition matrix elements) calculated using the quantum chemical EDMFs along with the Rydberg– Klein– Rees (RKR) potential, or ab initio potential, actually disagree with the experimental results. Therefore, more accurate theoretical calculations are needed.

In this work, we adopt a direct fit approach to determine an EDMF for the CO X¹Σ ⁺ state by utilizing individual, high-quality measurements for line intensities including the 5– 0 band. We also perform a series of theoretical calculations to determine the EDMF of the electronic state of CO (X¹Σ ⁺). Based on the RKR potential, the eigenfunctions, Ψ _{υ , J}(r), are determined by solving the radial Schrö dinger equation of nuclear motion. Eigenfunctions, Ψ _{υ , J}(r), and EDMFs are used to determine the vibrational matrix elements and the Herman– Wallis factors for several bands of CO (X¹Σ ⁺). Finally, we calculate the rovibrational line intensities of some bands of CO (X¹Σ ⁺) by using the present fitted and ab initio EDMFs and compare them with the published experimental data.

2. Theoretical basis

2.1. Fitted EDMF method

The method of obtaining the EDMF experimentally, as developed by Tipping and Herman, is to assume a power series expansion

and to fit the coefficient, M_i, to the measured rotationless transition matrix elements 〈 υ ′ , 0| M(r)| υ ″ , 0〉 .^[38] The single and double primes correspond to the upper and lower states, respectively. In Eq. (1), x = (r − r_e)/r_e, where r_e is the equilibrium separation and M₀ represents the permanent dipole moment at the minimum potential where r = r_e. In a harmonic potential, M₁x is related to the Δ υ = 1 transitions, while M₁x² is related to the Δ υ = 2 transitions and so on.

Using Eq. (1), the rovibrational matrix elements can be written as

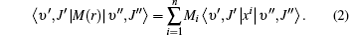
Thus, the inclusion of rotational components allows a better determination of the M_i coefficients by fitting to a greater number of points.^{[39, 40]} In order to derive the new EDMF from Eq. (2), we identify the best available experimental results for each band. We use the results of Zou et al.^[7] for the fundamental band, Brulat et al.’ s^[41] for the first overtone band, Sung et al.’ s^[17] for the 3– 0 band, Chackerian et al.’ s^[18] for the 4– 0 band, and Chung et al.’ s^[20] for the 5– 0 band. Moreover, in order to obtain the accurate coefficient M₀, the value of the matrix moment μ _{υ ′ = 0, υ ″ = 0} = 0.10982 Debye as reported by Chackerian et al.^[6] is also included in the fitting work. The weighted and unweighted fits of all data are performed.

2.2. Theoretical computational details

The ground state carbon monoxide molecule is a closed-shell molecule, and the electric configuration of the CO X¹Σ ⁺ is 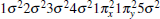, which has a₁ symmetry. We compute the EDMF by using highly correlated ab initio methods, namely, the complete active space self-consistent field (CASSCF)^[42] approach followed by the highly accurate averaged coupled-pair functional (ACPF)^[43] method in the C_2V point group.

The EDMF calculations are performed by using the MOLPRO 2009.1 program package, ^[44] with and without a finite-field approach with field values of ± 0.005 a.u. We separately use the aug-cc-pV6Z (aV6Z) and spdfghi aug-cc-pV6Z (spdfghi aV6Z) basis sets of Dunning et al. for both C and O atoms.^{[45– 47]} These basis sets are sufficiently diffuse to describe long-range interactions so that a more accurate EDMF can be determined at larger internuclear separations. In this work, we only consider the electric correlation energy of valence electrons and only choose the full valence active spaces consisting of eight valence orbitals, which is denoted by (4220) in C_2V point group symmetry.

With the aid of Le Roy’ s LEVEL 8.0 program, ^[48] the piecewise polynomial interpolation is performed by using numerical input potential energies and electric dipole moments. The rovibrational matrix elements are obtained through the use of the fitted EDMF and the theoretically calculated EDMF, together with an RKR potential energy function. The RKR potential curves for CO are constructed by using the purely numerical RKR method with Dunham coefficients from Velichko et al. who provided accurate molecular parameters for higher-lying vibrational levels (up to υ = 41).^{[49, 50]}

3. Results and discussion

3.1. Details of calculations and results

The RKR potential is employed to calculate the transition wavenumbers, lower-state energies, and the expectation values 〈 υ ′ , J′ | xⁱ| 0, J″ 〉 by using Le Roy’ s LEVEL 8.0 program.^[48] The rovibrational matrix elements are then evaluated from the measured line intensities according to

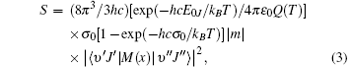
where S is the line intensity for pure ¹²C¹⁶O in cm^{− 1}/mol; h, c, and k are Planck constant, velocity of light, and Boltzmann constant, respectively; σ ₀ is the transition wavenumber in cm^{− 1}; T is the temperature; Q(T) is the total internal partition; m = 1/2[J′ (J′ + 1) − J″ (J″ + 1)] is a running number of values J″ + 1 for a line in branch R or − J″ for a line in branch P. A sequence of signs of the rovibrational matrix moments (+ − + − + + ) is adopted in a similar way to that in a previous study.^[20] Table 1 lists the rovibrational matrix elements derived from the experimental intensities and their experimental uncertainties. Finally, a fit of all listed rovibrational matrix elements to the system of linear Eq. (2) is carried out by using a least-squares fit program.^[51] Six coefficients of the EDMF, M₀, M₁, M₂, … , M₅, are determined, and the polynomial equation of the weighted EDMF is written as

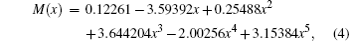
whereas the unweighted EDMF equation is

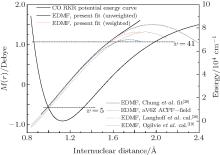
Both equations implement an equilibrium separation of r_e = 1.12822 Å obtained from the constructed RKR potential. For comparison, the determined fitted EDMFs and those reported by Chung et al. are plotted against internuclear distance in Fig. 1.^[20] Meanwhile, the theoretical EDMFs calculated through using the ACPF method at the aV6Z set level with the field values of ± 0.005 a.u., those by Langhoff and Bauschlicher^[36] through using the aug-cc-pVQZ ACPF-field method, and those by Ogilvie et al.^[19] through using the MCSCF method are all plotted in Fig. 1.

Table 1. Rovibrational transitional moments M_{υ 0}(m) of CO in units of Debye. The subscripts υ and 0 of M_{υ 0}(m) represent the υ -th upper vibrational level and the low vibrational level, respectively.

m	M₁₀(m)	M₂₀(m)	M₃₀(m)	M₄₀(m)	M₅₀(m)
− 25			– 3.64435× 10^{− 4}(1.15%)
– 24			– 3.73484× 10^{− 4}(1.15%)
– 23	– 1.08726× 10^{− 1}(3.56%)	6.1779× 10^{− 3}(0.75%)	– 3.61098× 10^{− 4}(1.15%)
– 22	– 1.06238× 10^{− 1}(3.56%)	6.2104× 10^{− 3}(0.75%)	– 3.62795× 10^{− 4}(1.15%)
– 21	– 1.07015× 10^{− 1}(3.56%)	6.2086× 10^{− 3}(0.75%)	– 3.71995× 10^{− 4}(1.15%)
– 20	– 1.06983× 10^{− 1}(3.56%)	6.2348× 10^{− 3}(0.75%)	– 3.70620× 10^{− 4}(1.15%)
– 19	– 1.07383× 10^{− 1}(3.56%)	6.2648× 10^{− 3}(0.75%)	– 3.72714× 10^{− 4}(1.15%)
– 18	– 1.06975× 10^{− 1}(3.56%)	6.2623× 10^{− 3}(0.75%)	– 3.75246× 10^{− 4}(1.15%)		1.60845× 10^{− 6}(7.50%)
– 17	– 1.07315× 10^{− 1}(3.56%)	6.2799× 10^{− 3}(0.75%)	– 3.77446× 10^{− 4}(1.15%)		2.04070× 10^{− 6}(7.50%)
– 16	– 1.06912× 10^{− 1}(3.56%)	6.2902× 10^{− 3}(0.75%)	– 3.78924× 10^{− 4}(1.15%)	1.53506× 10^{− 5}(1.12%)	1.85821× 10^{− 6}(7.50%)
– 15	– 1.06990× 10^{− 1}(3.56%)	6.3071× 10^{− 3}(0.75%)	– 3.82612× 10^{− 4}(1.15%)	1.66325× 10^{− 5}(1.12%)	1.63852× 10^{− 6}(7.50%)
– 14	– 1.07165× 10^{− 1}(3.56%)	6.3244× 10^{− 3}(0.75%)	– 3.83036× 10^{− 4}(1.15%)	1.59628× 10^{− 5}(1.12%)	2.13755× 10^{− 6}(7.50%)
– 13	– 1.06891× 10^{− 1}(3.56%)	6.3361× 10^{− 3}(0.75%)	– 3.85075× 10^{− 4}(1.15%)	1.63767× 10^{− 5}(1.12%)	1.86495× 10^{− 6}(7.50%)
– 12	– 1.07103× 10^{− 1}(3.56%)	6.3462× 10^{− 3}(0.75%)	– 3.87080× 10^{− 4}(1.15%)		1.81283× 10^{− 6}(7.50%)
– 11	– 1.06915× 10^{− 1}(3.56%)	6.3645× 10^{− 3}(0.75%)	– 3.90000× 10^{− 4}(1.15%)	1.63648× 10^{− 5}(1.12%)	1.80341× 10^{− 6}(7.50%)
– 10	– 1.06723× 10^{− 1}(3.56%)	6.3783× 10^{− 3}(0.75%)	– 3.91620× 10^{− 4}(1.15%)	1.67650× 10^{− 5}(1.12%)	1.51588× 10^{− 6}(7.50%)
– 9	– 1.06834× 10^{− 1}(3.56%)	6.3910× 10^{− 3}(0.75%)	– 3.93057× 10^{− 4}(1.15%)	1.72968× 10^{− 5}(1.12%)	1.23809× 10^{− 6}(7.50%)
– 8	– 1.06632× 10^{− 1}(3.56%)	6.4042× 10^{− 3}(0.75%)	– 3.95541× 10^{− 4}(1.15%)	1.79460× 10^{− 5}(1.12%)	1.27906× 10^{− 6}(7.50%)
– 7	– 1.06658× 10^{− 1}(3.56%)	6.4192× 10^{− 3}(0.75%)	– 3.97769× 10^{− 4}(1.15%)	1.79707× 10^{− 5}(1.12%)	1.19469× 10^{− 6}(7.50%)
– 6	– 1.06682× 10^{− 1}(3.56%)	6.4346× 10^{− 3}(0.75%)	– 4.00914× 10^{− 4}(1.15%)	1.84099× 10^{− 5}(1.12%)	1.39754× 10^{− 6}(7.50%)
– 5	– 1.06681× 10^{− 1}(3.56%)	6.4500× 10^{− 3}(0.75%)	– 4.03033× 10^{− 4}(1.15%)		1.13239× 10^{− 6}(7.50%)
– 4	– 1.06741× 10^{− 1}(3.56%)	6.4693× 10^{− 3}(0.75%)	– 4.05679× 10^{− 4}(1.15%)	1.88807× 10^{− 5}(1.12%)	1.02759× 10^{− 6}(7.50%)
– 3	– 1.07319× 10^{− 1}(3.56%)	6.4836× 10^{− 3}(0.75%)	– 4.09633× 10^{− 4}(1.15%)	1.89071× 10^{− 5}(1.12%)	1.13882× 10^{− 6}(7.50%)
– 2	– 1.06973× 10^{− 1}(3.56%)	6.5057× 10^{− 3}(0.75%)	– 4.09918× 10^{− 4}(1.15%)	1.93609× 10^{− 5}(1.12%)
– 1	– 1.06050× 10^{− 1}(3.56%)	6.5284× 10^{− 3}(0.75%)	– 4.12978× 10^{− 4}(1.15%)	2.04822× 10^{− 5}(1.12%)
1	– 1.06567× 10^{− 1}(3.56%)	6.5570× 10^{− 3}(0.75%)	– 4.17436× 10^{− 4}(1.15%)	2.05012× 10^{− 5}(1.12%)
2	– 1.06796× 10^{− 1}(3.56%)	6.5739× 10^{− 3}(0.75%)	– 4.20988× 10^{− 4}(1.15%)	2.10375× 10^{− 5}(1.12%)
3	– 1.06837× 10^{− 1}(3.56%)	6.5871× 10^{− 3}(0.75%)	– 4.23839× 10^{− 4}(1.15%)	2.18628× 10^{− 5}(1.12%)
4	– 1.06885× 10^{− 1}(3.56%)	6.6033× 10^{− 3}(0.75%)	– 4.25765× 10^{− 4}(1.15%)	2.18107× 10^{− 5}(1.12%)
5	– 1.06971× 10^{− 1}(3.56%)	6.6186× 10^{− 3}(0.75%)	– 4.27207× 10^{− 4}(1.15%)	2.22226× 10^{− 5}(1.12%)
6	– 1.06896× 10^{− 1}(3.56%)	6.6342× 10^{− 3}(0.75%)	– 4.29007× 10^{− 4}(1.15%)	2.26652× 10^{− 5}(1.12%)
7	– 1.07024× 10^{− 1}(3.56%)	6.6523× 10^{− 3}(0.75%)	– 4.31103× 10^{− 4}(1.15%)	2.27348× 10^{− 5}(1.12%)
8	– 1.07013× 10^{− 1}(3.56%)	6.6690× 10^{− 3}(0.75%)	– 4.32796× 10^{− 4}(1.15%)
9	– 1.06924× 10^{− 1}(3.56%)	6.6868× 10^{− 3}(0.75%)	– 4.34849× 10^{− 4}(1.15%)	2.33833× 10^{− 5}(1.12%)
10	– 1.07149× 10^{− 1}(3.56%)	6.7081× 10^{− 3}(0.75%)	– 4.39387× 10^{− 4}(1.15%)	2.33329× 10^{− 5}(1.12%)
11	– 1.07190× 10^{− 1}(3.56%)	6.7256× 10^{− 3}(0.75%)	– 4.42360× 10^{− 4}(1.15%)	2.41239× 10^{− 5}(1.12%)
12	– 1.07395× 10^{− 1}(3.56%)	6.7442× 10^{− 3}(0.75%)	– 4.44085× 10^{− 4}(1.15%)	2.50118× 10^{− 5}(1.12%)
13	– 1.07425× 10^{− 1}(3.56%)	6.7650× 10^{− 3}(0.75%)	– 4.49534× 10^{− 4}(1.15%)	2.48110× 10^{− 5}(1.12%)
14	– 1.07512× 10^{− 1}(3.56%)	6.7867× 10^{− 3}(0.75%)	– 4.51383× 10^{− 4}(1.15%)	2.52936× 10^{− 5}(1.12%)
15	– 1.07630× 10^{− 1}(3.56%)	6.8046× 10^{− 3}(0.75%)	– 4.55507× 10^{− 4}(1.15%)
16	– 1.07721× 10^{− 1}(3.56%)	6.8255× 10^{− 3}(0.75%)	– 4.58738× 10^{− 4}(1.15%)	2.59868× 10^{− 5}(1.12%)
17	– 1.07670× 10^{− 1}(3.56%)	6.8486× 10^{− 3}(0.75%)	– 4.60818× 10^{− 4}(1.15%)
18	– 1.07456× 10^{− 1}(3.56%)	6.8658× 10^{− 3}(0.75%)	– 4.64357× 10^{− 4}(1.15%)
19	– 1.08000× 10^{− 1}(3.56%)	6.8886× 10^{− 3}(0.75%)	– 4.67094× 10^{− 4}(1.15%)
20	– 1.08020× 10^{− 1}(3.56%)	6.9086× 10^{− 3}(0.75%)	– 4.71070× 10^{− 4}(1.15%)
21	– 1.08247× 10^{− 1}(3.56%)	6.9296× 10^{− 3}(0.75%)	– 4.72801× 10^{− 4}(1.15%)
22	– 1.08250× 10^{− 1}(3.56%)	6.9462× 10^{− 3}(0.75%)	– 4.77859× 10^{− 4}(1.15%)
23	– 1.08915× 10^{− 1}(3.56%)	6.9589× 10^{− 3}(0.75%)	– 4.77188× 10^{− 4}(1.15%)
24	– 1.09055× 10^{− 1}(3.56%)		– 4.78968× 10^{− 4}(1.15%)

	Figure Option View Download New Window
	Fig. 1. Electric dipole moment functions and RKR potential energy curve.

Within the respective valid range, the three fitted EDMFs are in close agreement with each other. According to the RKR potential, the classical turning points of the vibrational level υ = 5 are found to be approximately 0.967 Å and 1.322 Å . Therefore, the fitted EDMF is most reliable in the region between these two limits, which are slightly different from the results shown in Chung et al. (0.99 Å and 1.33 Å ).^[20] The valid range of the fitted EDMF is controlled by the largest overtones which are very sensitive to determining the higher coefficients of M_i in Eq. (1). Thus, it is important to obtain experimental measurements for the largest possible values of υ ′ and Δ υ . The weighted and unweighted fitted EDMFs overlap together at 0.85 Å ≤ r ≤ 1.45 Å in the present work. In the valid range, all the fitted EDMFs agree well with the theoretical EDMF calculated using the ACPF method with a finite-field ± 0.005 a.u at the aV6Z basis set level (aV6Z ACPF-field). They also agree well with the theoretical results of Langhoff and Bauschlicher.^[36] The three lines outside the valid range are not consistent with the two theoretical EDMFs at large internuclear distances. Actually, the degree of agreement between the fitted EDMF of Chung et al. and the two theoretical EDMFs become continually worse when r ≥ 1.33 Å .

3.2. Theoretical results of EDMFs

According to geometrical optimization of the CO molecule, the equilibrium separation and the minimum energy are 1.1324 Å and − 113.197964 a.u. for the aV6Z basis set, and 1.1323 Å and − 113.198196 a.u for the spdfghi aV6Z basis set, respectively. These two values of r_e agree well with the experimental values of 1.1283 Å and 1.1282 Å obtained from the constructed RKR potential in the present work.^[52] The calculated energies and dipole moments each as a function of r are listed in Table 2 at the ACPF (4220) level using the aV6Z and spdfghi aV6Z basis sets. The two EDMFs almost converge both with and without using the finite-field approach. Here, we only compare the aV6Z ACPF-field EDMF with the three fitted and previous theoretical ones in Fig. 1.

Table 2. Energies and electric dipole moments (EDMs) (a.u.)^a for the X¹Σ ⁺ state CO using the aug– cc– pV6Z and spdfgh aug– cc– pV6Z basis sets.

r(a₀)	aV6Z			spdfghi aV6Z
r(a₀)		Energy/a.u.	EDM	EDM (field)	Energy/a.u.	EDM	EDM (field)
1.5022	– 112.594710	– 0.434729	– 0.538579	– 112.597530	– 0.432539	– 0.538746
1.5396	– 112.694260	– 0.416295	– 0.526169	– 112.697154	– 0.413896	– 0.526399
1.5771	– 112.779349	– 0.404725	– 0.426192	– 112.784017	– 0.395134	– 0.440991
1.6129	– 112.849758	– 0.385034	– 0.392749	– 112.852724	– 0.381194	– 0.392764
1.6564	– 112.922746	– 0.360298	– 0.367594	– 112.925744	– 0.356304	– 0.367608
1.6932	– 112.974897	– 0.338773	– 0.345766	– 112.977921	– 0.334650	– 0.345780
1.7299	– 113.019118	– 0.316863	– 0.323584	– 113.022169	– 0.312614	– 0.323597
1.7606	– 113.051005	– 0.298063	– 0.304616	– 113.054078	– 0.293758	– 0.304628
1.7990	– 113.084844	– 0.274235	– 0.280528	– 113.087944	– 0.269806	– 0.280539
1.8224	– 113.102516	– 0.259524	– 0.265659	– 113.105632	– 0.255022	– 0.265670
1.8498	– 113.120705	– 0.242073	– 0.248020	– 113.123841	– 0.237484	– 0.248030
1.8832	– 113.139432	– 0.220618	– 0.226331	– 113.142591	– 0.215926	– 0.226341
1.9264	– 113.158734	– 0.192552	– 0.197949	– 113.161924	– 0.187730	– 0.197959
1.9907	– 113.178715	– 0.150241	– 0.155138	– 113.181949	– 0.145231	– 0.155146
2.0203	– 113.184896	– 0.130654	– 0.135304	– 113.188149	– 0.125561	– 0.135313
2.0472	– 113.189104	– 0.112747	– 0.117171	– 113.192376	– 0.107502	– 0.117180
2.0930	– 113.193494	– 0.082217	– 0.086238	– 113.196797	– 0.076842	– 0.086246
2.1735	– 113.194179	– 0.028640	– 0.031914	– 113.197536	– 0.023047	– 0.031921
2.2276	– 113.190630	0.007105	0.004354	– 113.194024	0.012835	0.004348
2.2628	– 113.186938	0.030311	0.027802	– 113.190356	0.036040	0.027796
2.3048	– 113.181341	0.057660	0.055558	– 113.184788	0.063478	0.055553
2.4112	– 113.162691	0.125508	0.124413	– 113.166209	0.131494	0.124408
2.4974	– 113.144321	0.178495	0.178223	– 113.147899	0.184669	0.178219
2.5748	– 113.126332	0.224230	0.224670	– 113.129961	0.230504	0.224667
2.6473	– 113.108754	0.265272	0.266354	– 113.112432	0.271622	0.266352
2.7169	– 113.091603	0.302829	0.304503	– 113.095327	0.309239	0.304502
2.7846	– 113.074884	0.337664	0.339788	– 113.078653	0.344024	0.339789
2.8511	– 113.058602	0.370032	0.372609	– 113.062416	0.376429	0.372611
2.9170	– 113.042757	0.400190	0.403210	– 113.046615	0.406612	0.403215
2.9826	– 113.027352	0.428309	0.431728	– 113.031253	0.434840	0.431735
3.0483	– 113.012384	0.454454	0.458231	– 113.016329	0.460998	0.458241
3.1143	– 112.997852	0.478616	0.482739	– 113.001840	0.485196	0.482751
3.1810	– 112.983754	0.500774	0.505215	– 112.987785	0.507406	0.505228
3.2484	– 112.970089	0.520847	0.525579	– 112.974163	0.527593	0.525594
3.3167	– 112.956859	0.539021	0.543707	– 112.960975	0.545584	0.543724
3.3863	– 112.944062	0.554580	0.559440	– 112.948221	0.561197	0.559459
3.4572	– 112.931700	0.567516	0.572564	– 112.935901	0.574287	0.572584
3.5298	– 112.919774	0.577580	0.582850	– 112.924016	0.584470	0.582870
3.6042	– 112.908286	0.584327	0.589987	– 112.912569	0.591417	0.590005
3.6806	– 112.897239	0.587511	0.593662	– 112.901561	0.594701	0.593680
3.7595	– 112.886635	0.586470	0.593498	– 112.890995	0.594123	0.593515
3.8411	– 112.876480	0.580907	0.589076	– 112.880875	0.588810	0.589090
3.9259	– 112.866780	0.570119	0.579950	– 112.871206	0.578305	0.579960
4.0143	– 112.857540	0.553588	0.565654	– 112.861993	0.562088	0.565660
4.1070	– 112.848771	0.530930	0.545731	– 112.853245	0.539840	0.545731
4.2047	– 112.840482	0.501952	0.519776	– 112.844971	0.510937	0.519768
4.3084	– 112.832687	0.466245	0.487520	– 112.837182	0.475143	0.487503
4.4195	– 112.825401	0.424333	0.448937	– 112.829894	0.433342	0.448909
4.5396	– 112.818642	0.377221	0.404351	– 112.823123	0.385900	0.404314
4.6711	– 112.812428	0.325645	0.354639	– 112.816888	0.333875	0.354594
4.8172	– 112.806776	0.271049	0.301427	– 112.811208	0.278671	0.301378
4.9828	– 112.801702	0.215163	0.196298	– 112.806097	0.221749	0.196166

A minus sign implies C⁻O⁺ polarity.

Table 2. Energies and electric dipole moments (EDMs) (a.u.)^a for the X¹Σ ⁺ state CO using the aug– cc– pV6Z and spdfgh aug– cc– pV6Z basis sets.

The aV6Z ACPF-field EDMF agrees well with the three fitted ones in their valid ranges. Compared with the theoretical results given by Langhoff and Bauschlicher, ^[36] the values of the dipole moments are smaller at small r and slightly larger at large r. The latest work of Oglivie et al.^[19] disagrees with the three fitted and the two theoretical ones.

3.3. Calculations of transition matrix moments

First, by combining the RKR potential and the EDMFs of Chung et al., ^[20] and Langhoff and Bauschlicher, ^[36] and the present fits, we calculate the rovibrational matrix moments and vibrational matrix moments. In Table 3, the absolute values of some vibrational matrix elements μ _{υ ′ , υ ″} are compared with the experimental results. The values | μ _{υ ′ , υ ″}| calculated using the present unweighted fitted EDMF agree well with the experimental values at the bands υ ′ – 0 (υ ′ = 0– 5). Though the values derived using the weighted fitted EDMF also agree well with the measurements at the bands υ ′ – 0 (υ ′ = 0– 4), the value | μ _{5 − 0}| = 2.471 × 10^{− 6} Debye deviates largely from the experimental value of 1.079 × 10^{− 6} Debye. One possible reason is that Chung et al. did not specify the experimental uncertainty and only provided a minimum uncertainty of about 15% for all measured line intensities in their work.^[20] Thus, only the unweighted fitted EDMF will be considered when comparing line intensities later in the article.

Table 3. Vibrational dipole moments | μ _{υ ′ , υ ″}| (in Debye) computed by combining the RKR potential and the EDMFs for vibrational bands of CO.

Further, we calculate vibrational dipole moments by combining the ab initio potential and the ab initio electric dipole moments for the ground state CO in Table 4. Without a finite-field, both the results of the aV6Z and spdfghi aV6Z EDMFs only agree well with the experimental values in the bands υ ′ – 0 (υ ′ = 0– 3). When adding the finite-field, the values μ _{υ ′ , υ ″} agree well with measurements not only in the bands υ ′ – 0 (υ ′ = 0– 3) but also in the 4– 0 and 5– 0 bands. The vibrational dipole moments, calculated using the aV6Z ACPF-field EDMF, seems better than using the spdfghi aV6Z ACPF-field EDMF. Thus, the aV6Z ACPF-field EDMF is used to compute the rovibrational transition moments and line intensities by combining the RKR potential. In Table 3, by comparing the μ _{υ ′ , υ ″} calculated using the aV6Z ACPF-field EDMF and the EDMF of Langhoff et al. with experimental results, it is clear that our μ _{υ ′ , υ ″} is in better agreement with the experimental results except the value of μ _{0, 0}. Relative to the approach without the finite-field, the variation of the electric dipole moment calculated using a finite-field approach is larger at the equilibrium separation than at other separations. This may be the reason why the value μ _{0, 0} is so much different from the fitted ones.

Table 4. Vibrational dipole moments μ _{υ ′ , υ ″} (Debye) computed by combining the ab initio potential and the ab initio electric dipole moments for the ground state CO.

υ ′ – υ ″	aV6Z	aV6Z (field)	spdfgh aV6Z	spdfgh aV6Z (field)	υ ′ – υ ″	aV6Z	aV6Z (field)	spdfgh aV6Z	spdfgh aV6Z (field)
0– 0	1.0300× 10^{− 1}	1.2590× 10^{− 1}	1.0302× 10^{− 1}	1.2596× 10^{− 1}
1– 1	7.7193× 10^{− 2}	9.9759× 10^{− 2}	7.7213× 10^{− 2}	9.9816× 10^{− 2}	1– 0	– 1.0832× 10^{− 1}	– 1.0939× 10^{− 1}	– 1.0832× 10^{− 1}	– 1.0939× 10^{− 1}
2– 2	5.1363× 10^{− 2}	7.3546× 10^{− 2}	5.1381× 10^{− 2}	7.3600× 10^{− 2}	2– 1	– 1.5307× 10^{− 1}	– 1.5458× 10^{− 1}	– 1.5307× 10^{− 1}	– 1.5458× 10^{− 1}
3– 3	2.5438× 10^{− 2}	4.7266× 10^{− 2}	2.5457× 10^{− 2}	4.7318× 10^{− 2}	3– 2	– 1.8727× 10^{− 1}	– 1.8913× 10^{− 1}	– 1.8727× 10^{− 1}	– 1.8914× 10^{− 1}
4– 4	– 5.8012× 10^{− 4}	2.0928× 10^{− 2}	– 5.6199× 10^{− 4}	2.0978× 10^{− 2}	4– 3	– 2.1593× 10^{− 1}	– 2.1812× 10^{− 1}	– 2.1593× 10^{− 1}	– 2.1813× 10^{− 1}
5– 5	– 2.6627× 10^{− 2}	– 5.4637× 10^{− 3}	– 2.6609× 10^{− 2}	– 5.4155× 10^{− 3}	5– 4	– 2.4105× 10^{− 1}	– 2.4351× 10^{− 1}	– 2.4104× 10^{− 1}	– 2.4351× 10^{− 1}
6– 6	– 5.2716× 10^{− 2}	– 3.1896× 10^{− 2}	– 5.2697× 10^{− 2}	– 3.1849× 10^{− 2}	6– 5	– 2.6359× 10^{− 1}	– 2.6629× 10^{− 1}	– 2.6359× 10^{− 1}	– 2.6630× 10^{− 1}
7– 7	– 7.8836× 10^{− 2}	– 5.8361× 10^{− 2}	– 7.8817× 10^{− 2}	– 5.8315× 10^{− 2}	7– 6	– 2.8413× 10^{− 1}	– 2.8707× 10^{− 1}	– 2.8412× 10^{− 1}	– 2.8707× 10^{− 1}
8– 8	– 1.0498× 10^{− 1}	– 8.4853× 10^{− 2}	– 1.0496× 10^{− 1}	– 8.4809× 10^{− 2}	8– 7	– 3.0304× 10^{− 1}	– 3.0621× 10^{− 1}	– 3.0303× 10^{− 1}	– 3.0621× 10^{− 1}
9– 9	– 1.3114× 10^{− 1}	– 1.1137× 10^{− 1}	– 1.3112× 10^{− 1}	– 1.1132× 10^{− 1}	9– 8	– 3.2059× 10^{− 1}	– 3.2398× 10^{− 1}	– 3.2058× 10^{− 1}	– 3.2399× 10^{− 1}
10– 10	– 1.5731× 10^{− 1}	– 1.3789× 10^{− 1}	– 1.5729× 10^{− 1}	– 1.3785× 10^{− 1}	10– 9	– 3.3697× 10^{− 1}	– 3.4057× 10^{− 1}	– 3.3696× 10^{− 1}	– 3.4057× 10^{− 1}
11– 11	– 1.8349× 10^{− 1}	– 1.6442× 10^{− 1}	– 1.8347× 10^{− 1}	– 1.6438× 10^{− 1}	11– 10	– 3.5232× 10^{− 1}	– 3.5611× 10^{− 1}	– 3.5231× 10^{− 1}	– 3.5612× 10^{− 1}
12– 12	– 2.0965× 10^{− 1}	– 1.9094× 10^{− 1}	– 2.0963× 10^{− 1}	– 1.9090× 10^{− 1}	12– 11	– 3.6674× 10^{− 1}	– 3.7072× 10^{− 1}	– 3.6672× 10^{− 1}	– 3.7073× 10^{− 1}
13– 13	– 2.3579× 10^{− 1}	– 2.1743× 10^{− 1}	– 2.3577× 10^{− 1}	– 2.1740× 10^{− 1}	13– 12	– 3.8031× 10^{− 1}	– 3.8448× 10^{− 1}	– 3.8029× 10^{− 1}	– 3.8449× 10^{− 1}
14– 14	– 2.6191× 10^{− 1}	– 2.4390× 10^{− 1}	– 2.6189× 10^{− 1}	– 2.4387× 10^{− 1}	14– 13	– 3.9310× 10^{− 1}	– 3.9744× 10^{− 1}	– 3.9308× 10^{− 1}	– 3.9745× 10^{− 1}
15– 15	– 2.8799× 10^{− 1}	– 2.7033× 10^{− 1}	– 2.8797× 10^{− 1}	– 2.7030× 10^{− 1}	15– 14	– 4.0516× 10^{− 1}	– 4.0966× 10^{− 1}	– 4.0514× 10^{− 1}	– 4.0967× 10^{− 1}
16– 16	– 3.1403× 10^{− 1}	– 2.9671× 10^{− 1}	– 3.1401× 10^{− 1}	– 2.9668× 10^{− 1}	16– 15	– 4.1653× 10^{− 1}	– 4.2119× 10^{− 1}	– 4.1652× 10^{− 1}	– 4.2120× 10^{− 1}
17– 17	– 3.4000× 10^{− 1}	– 3.2302× 10^{− 1}	– 3.3998× 10^{− 1}	– 3.2300× 10^{− 1}	17– 16	– 4.2725× 10^{− 1}	– 4.3204× 10^{− 1}	– 4.2723× 10^{− 1}	– 4.3206× 10^{− 1}
18– 18	– 3.6591× 10^{− 1}	– 3.4926× 10^{− 1}	– 3.6589× 10^{− 1}	– 3.4924× 10^{− 1}	18– 17	– 4.3733× 10^{− 1}	– 4.4226× 10^{− 1}	– 4.3731× 10^{− 1}	– 4.4227× 10^{− 1}
19– 19	– 3.9173× 10^{− 1}	– 3.7541× 10^{− 1}	– 3.9172× 10^{− 1}	– 3.7539× 10^{− 1}	19– 18	– 4.4680× 10^{− 1}	– 4.5185× 10^{− 1}	– 4.4679× 10^{− 1}	– 4.5187× 10^{− 1}
20– 20	– 4.1746× 10^{− 1}	– 4.0145× 10^{− 1}	– 4.1745× 10^{− 1}	– 4.0144× 10^{− 1}	20– 19	– 4.5569× 10^{− 1}	– 4.6084× 10^{− 1}	– 4.5567× 10^{− 1}	– 4.6085× 10^{− 1}
21– 21	– 4.4307× 10^{− 1}	– 4.2738× 10^{− 1}	– 4.4305× 10^{− 1}	– 4.2737× 10^{− 1}	21– 20	– 4.6398× 10^{− 1}	– 4.6923× 10^{− 1}	– 4.6396× 10^{− 1}	– 4.6925× 10^{− 1}
22– 22	– 4.6853× 10^{− 1}	– 4.5317× 10^{− 1}	– 4.6852× 10^{− 1}	– 4.5316× 10^{− 1}	22– 21	– 4.7168× 10^{− 1}	– 4.7703× 10^{− 1}	– 4.7166× 10^{− 1}	– 4.7705× 10^{− 1}
23– 23	– 4.9384× 10^{− 1}	– 4.7880× 10^{− 1}	– 4.9383× 10^{− 1}	– 4.7880× 10^{− 1}	23– 22	– 4.7880× 10^{− 1}	– 4.8425× 10^{− 1}	– 4.7878× 10^{− 1}	– 4.8427× 10^{− 1}
24– 24	– 5.1899× 10^{− 1}	– 5.0426× 10^{− 1}	– 5.1898× 10^{− 1}	– 5.0426× 10^{− 1}	24– 23	– 4.8535× 10^{− 1}	– 4.9089× 10^{− 1}	– 4.8533× 10^{− 1}	– 4.9091× 10^{− 1}
25– 25	– 5.4396× 10^{− 1}	– 5.2954× 10^{− 1}	– 5.4394× 10^{− 1}	– 5.2954× 10^{− 1}	25– 24	– 4.9133× 10^{− 1}	– 4.9694× 10^{− 1}	– 4.9131× 10^{− 1}	– 4.9696× 10^{− 1}
26– 26	– 5.6872× 10^{− 1}	– 5.5460× 10^{− 1}	– 5.6870× 10^{− 1}	– 5.5459× 10^{− 1}	26– 25	– 4.9673× 10^{− 1}	– 5.0241× 10^{− 1}	– 4.9671× 10^{− 1}	– 5.0243× 10^{− 1}
27– 27	– 5.9326× 10^{− 1}	– 5.7942× 10^{− 1}	– 5.9323× 10^{− 1}	– 5.7941× 10^{− 1}	27– 26	– 5.0154× 10^{− 1}	– 5.0727× 10^{− 1}	– 5.0153× 10^{− 1}	– 5.0730× 10^{− 1}
2– 0	6.5975× 10^{− 3}	6.6076× 10^{− 3}	6.5980× 10^{− 3}	6.6081× 10^{− 3}
3– 1	1.1604× 10^{− 2}	1.1587× 10^{− 2}	1.1605× 10^{− 2}	1.1588× 10^{− 2}	3– 0	– 4.3002× 10^{− 4}	– 4.1623× 10^{− 4}	– 4.3025× 10^{− 4}	– 4.1648× 10^{− 4}
4– 2	1.6600× 10^{− 2}	1.6592× 10^{− 2}	1.6601× 10^{− 2}	1.6593× 10^{− 2}	4– 1	– 8.9315× 10^{− 4}	– 8.5829× 10^{− 4}	– 8.9344× 10^{− 4}	– 8.5860× 10^{− 4}
5– 3	2.1643× 10^{− 2}	2.1683× 10^{− 2}	2.1644× 10^{− 2}	2.1684× 10^{− 2}	5– 2	– 1.4294× 10^{− 3}	– 1.4008× 10^{− 3}	– 1.4301× 10^{− 3}	– 1.4013× 10^{− 3}
6– 4	2.6809× 10^{− 2}	2.6872× 10^{− 2}	2.6810× 10^{− 2}	2.6873× 10^{− 2}	6– 3	– 2.0851× 10^{− 3}	– 2.0406× 10^{− 3}	– 2.0859× 10^{− 3}	– 2.0413× 10^{− 3}
7– 5	3.2076× 10^{− 2}	3.2165× 10^{− 2}	3.2077× 10^{− 2}	3.2166× 10^{− 2}	7– 4	– 2.8417× 10^{− 3}	– 2.7788× 10^{− 3}	– 2.8425× 10^{− 3}	– 2.7797× 10^{− 3}
8– 6	3.7444× 10^{− 2}	3.7562× 10^{− 2}	3.7445× 10^{− 2}	3.7563× 10^{− 2}	8– 5	– 3.6819× 10^{− 3}	– 3.6169× 10^{− 3}	– 3.6827× 10^{− 3}	– 3.6179× 10^{− 3}
9– 7	4.2912× 10^{− 2}	4.3062× 10^{− 2}	4.2913× 10^{− 2}	4.3063× 10^{− 2}	9– 6	– 4.6174× 10^{− 3}	– 4.5557× 10^{− 3}	– 4.6184× 10^{− 3}	– 4.5568× 10^{− 3}
10– 8	4.8479× 10^{− 2}	4.8662× 10^{− 2}	4.8480× 10^{− 2}	4.8663× 10^{− 2}	10– 7	– 5.6589× 10^{− 3}	– 5.5969× 10^{− 3}	– 5.6600× 10^{− 3}	– 5.5980× 10^{− 3}
11– 9	5.4140× 10^{− 2}	5.4361× 10^{− 2}	5.4141× 10^{− 2}	5.4362× 10^{− 2}	11– 8	– 6.8089× 10^{− 3}	– 6.7417× 10^{− 3}	– 6.8102× 10^{− 3}	– 6.7429× 10^{− 3}
12– 10	5.9891× 10^{− 2}	6.0155× 10^{− 2}	5.9892× 10^{− 2}	6.0156× 10^{− 2}	12– 9	– 8.0621× 10^{− 3}	– 7.9920× 10^{− 3}	– 8.0634× 10^{− 3}	– 7.9932× 10^{− 3}
13– 11	6.5732× 10^{− 2}	6.6041× 10^{− 2}	6.5733× 10^{− 2}	6.6042× 10^{− 2}	13– 10	– 9.4197× 10^{− 3}	– 9.3488× 10^{− 3}	– 9.4211× 10^{− 3}	– 9.3501× 10^{− 3}
14– 12	7.1656× 10^{− 2}	7.2014× 10^{− 2}	7.1657× 10^{− 2}	7.2016× 10^{− 2}	14– 11	– 1.0886× 10^{− 2}	– 1.0814× 10^{− 2}	– 1.0887× 10^{− 2}	– 1.0815× 10^{− 2}
15– 13	7.7657× 10^{− 2}	7.8074× 10^{− 2}	7.7658× 10^{− 2}	7.8076× 10^{− 2}	15– 12	– 1.2463× 10^{− 2}	– 1.2388× 10^{− 2}	– 1.2465× 10^{− 2}	– 1.2389× 10^{− 2}
16– 14	8.3731× 10^{− 2}	8.4216× 10^{− 2}	8.3732× 10^{− 2}	8.4218× 10^{− 2}	16– 13	– 1.4155× 10^{− 2}	– 1.4073× 10^{− 2}	– 1.4156× 10^{− 2}	– 1.4075× 10^{− 2}
17– 15	8.9881× 10^{− 2}	9.0436× 10^{− 2}	8.9882× 10^{− 2}	9.0438× 10^{− 2}	17– 14	– 1.5958× 10^{− 2}	– 1.5871× 10^{− 2}	– 1.5960× 10^{− 2}	– 1.5873× 10^{− 2}
18– 16	9.6104× 10^{− 2}	9.6730× 10^{− 2}	9.6106× 10^{− 2}	9.6732× 10^{− 2}	18– 15	– 1.7869× 10^{− 2}	– 1.7783× 10^{− 2}	– 1.7871× 10^{− 2}	– 1.7785× 10^{− 2}
19– 17	1.0239× 10^{− 1}	1.0310× 10^{− 1}	1.0239× 10^{− 1}	1.0310× 10^{− 1}	19– 16	– 1.9892× 10^{− 2}	– 1.9809× 10^{− 2}	– 1.9894× 10^{− 2}	– 1.9811× 10^{− 2}
20– 18	1.0874× 10^{− 1}	1.0953× 10^{− 1}	1.0874× 10^{− 1}	1.0953× 10^{− 1}	20– 17	– 2.2034× 10^{− 2}	– 2.1951× 10^{− 2}	– 2.2037× 10^{− 2}	– 2.1954× 10^{− 2}
21– 19	1.1514× 10^{− 1}	1.1603× 10^{− 1}	1.1514× 10^{− 1}	1.1603× 10^{− 1}	21– 18	– 2.4294× 10^{− 2}	– 2.4209× 10^{− 2}	– 2.4297× 10^{− 2}	– 2.4212× 10^{− 2}
22– 20	1.2162× 10^{− 1}	1.2259× 10^{− 1}	1.2162× 10^{− 1}	1.2259× 10^{− 1}	22– 19	– 2.6658× 10^{− 2}	– 2.6584× 10^{− 2}	– 2.6662× 10^{− 2}	– 2.6587× 10^{− 2}
23– 21	1.2816× 10^{− 1}	1.2921× 10^{− 1}	1.2816× 10^{− 1}	1.2921× 10^{− 1}	23– 20	– 2.9127× 10^{− 2}	– 2.9077× 10^{− 2}	– 2.9131× 10^{− 2}	– 2.9080× 10^{− 2}
24– 22	1.3474× 10^{− 1}	1.3588× 10^{− 1}	1.3475× 10^{− 1}	1.3588× 10^{− 1}	24– 21	– 3.1710× 10^{− 2}	– 3.1687× 10^{− 2}	– 3.1714× 10^{− 2}	– 3.1690× 10^{− 2}
25– 23	1.4138× 10^{− 1}	1.4260× 10^{− 1}	1.4138× 10^{− 1}	1.4260× 10^{− 1}	25– 22	– 3.4415× 10^{− 2}	– 3.4417× 10^{− 2}	– 3.4420× 10^{− 2}	– 3.4420× 10^{− 2}
26– 24	1.4805× 10^{− 1}	1.4937× 10^{− 1}	1.4805× 10^{− 1}	1.4937× 10^{− 1}	26– 23	– 3.7238× 10^{− 2}	– 3.7265× 10^{− 2}	– 3.7243× 10^{− 2}	– 3.7268× 10^{− 2}
27– 25	1.5477× 10^{− 1}	1.5618× 10^{− 1}	1.5477× 10^{− 1}	1.5619× 10^{− 1}	27– 24	– 4.0179× 10^{− 2}	– 4.0232× 10^{− 2}	– 4.0183× 10^{− 2}	– 4.0234× 10^{− 2}
4– 0	4.3121× 10^{− 5}	2.0117× 10^{− 5}	4.3239× 10^{− 5}	2.0109× 10^{− 5}
5– 1	6.4749× 10^{− 5}	5.0673× 10^{− 5}	6.4853× 10^{− 5}	5.0835× 10^{− 5}	5– 0	– 1.3562× 10^{− 5}	1.5796× 10^{− 6}	– 1.3569× 10^{− 5}	1.6439× 10^{− 6}
6– 2	8.2069× 10^{− 5}	9.6781× 10^{− 5}	8.2208× 10^{− 5}	9.7039× 10^{− 5}	6– 1	4.2863× 10^{− 6}	1.1173× 10^{− 6}	4.1952× 10^{− 6}	1.1258× 10^{− 6}
7– 3	1.5700× 10^{− 4}	1.5733× 10^{− 4}	1.5716× 10^{− 4}	1.5755× 10^{− 4}	7– 2	9.3291× 10^{− 6}	1.2481× 10^{− 6}	9.3150× 10^{− 6}	1.1530× 10^{− 6}
8– 4	2.5286× 10^{− 4}	2.3848× 10^{− 4}	2.5303× 10^{− 4}	2.3871× 10^{− 4}	8– 3	5.7541× 10^{− 6}	1.0362× 10^{− 6}	5.8363× 10^{− 6}	8.7791× 10^{− 7}
9– 5	3.6570× 10^{− 4}	3.4242× 10^{− 4}	3.6595× 10^{− 4}	3.4275× 10^{− 4}	9– 4	8.4889× 10^{− 6}	– 1.7618× 10^{− 6}	8.5743× 10^{− 6}	– 1.8874× 10^{− 6}
10– 6	4.9963× 10^{− 4}	4.7076× 10^{− 4}	4.9997× 10^{− 4}	4.7117× 10^{− 4}	10– 5	5.6864× 10^{− 6}	– 7.5951× 10^{− 6}	5.6996× 10^{− 6}	– 7.6883× 10^{− 6}
11– 7	6.6072× 10^{− 4}	6.2627× 10^{− 4}	6.6110× 10^{− 4}	6.2670× 10^{− 4}	11– 6	– 7.5834× 10^{− 6}	– 1.6902× 10^{− 5}	– 7.6435× 10^{− 6}	– 1.6985× 10^{− 5}
12– 8	8.5183× 10^{− 4}	8.1260× 10^{− 4}	8.5220× 10^{− 4}	8.1302× 10^{− 4}	12– 7	– 2.9432× 10^{− 5}	– 3.0188× 10^{− 5}	– 2.9530× 10^{− 5}	– 3.0258× 10^{− 5}
13– 9	1.0758× 10^{− 3}	1.0329× 10^{− 3}	1.0762× 10^{− 3}	1.0334× 10^{− 3}	13– 8	– 5.3416× 10^{− 5}	– 4.8833× 10^{− 5}	– 5.3504× 10^{− 5}	– 4.8891× 10^{− 5}
14– 10	1.3370× 10^{− 3}	1.2899× 10^{− 3}	1.3374× 10^{− 3}	1.2904× 10^{− 3}	14– 9	– 8.1836× 10^{− 5}	– 7.4069× 10^{− 5}	– 8.1896× 10^{− 5}	– 7.4121× 10^{− 5}
15– 11	1.6373× 10^{− 3}	1.5867× 10^{− 3}	1.6378× 10^{− 3}	1.5873× 10^{− 3}	15– 10	– 1.1912× 10^{− 4}	– 1.0720× 10^{− 4}	– 1.1915× 10^{− 4}	– 1.0726× 10^{− 4}
16– 12	1.9772× 10^{− 3}	1.9269× 10^{− 3}	1.9778× 10^{− 3}	1.9276× 10^{− 3}	16– 11	– 1.6789× 10^{− 4}	– 1.4968× 10^{− 4}	– 1.6790× 10^{− 4}	– 1.4977× 10^{− 4}
17– 13	2.3626× 10^{− 3}	2.3135× 10^{− 3}	2.3634× 10^{− 3}	2.3143× 10^{− 3}	17– 12	– 2.2786× 10^{− 4}	– 2.0335× 10^{− 4}	– 2.2790× 10^{− 4}	– 2.0350× 10^{− 4}
18– 14	2.8027× 10^{− 3}	2.7498× 10^{− 3}	2.8037× 10^{− 3}	2.7507× 10^{− 3}	18– 13	– 2.9749× 10^{− 4}	– 2.7016× 10^{− 4}	– 2.9761× 10^{− 4}	– 2.7035× 10^{− 4}
19– 15	3.3002× 10^{− 3}	3.2393× 10^{− 3}	3.3013× 10^{− 3}	3.2404× 10^{− 3}	19– 14	– 3.7761× 10^{− 4}	– 3.5210× 10^{− 4}	– 3.7784× 10^{− 4}	– 3.5232× 10^{− 4}
20– 16	3.8510× 10^{− 3}	3.7858× 10^{− 3}	3.8523× 10^{− 3}	3.7870× 10^{− 3}	20– 15	– 4.7599× 10^{− 4}	– 4.5103× 10^{− 4}	– 4.7635× 10^{− 4}	– 4.5130× 10^{− 4}
21– 17	4.4579× 10^{− 3}	4.3929× 10^{− 3}	4.4594× 10^{− 3}	4.3942× 10^{− 3}	21– 16	– 5.9908× 10^{− 4}	– 5.6895× 10^{− 4}	– 5.9959× 10^{− 4}	– 5.6931× 10^{− 4}
22– 18	5.1341× 10^{− 3}	5.0639× 10^{− 3}	5.1359× 10^{− 3}	5.0653× 10^{− 3}	22– 17	– 7.4290× 10^{− 4}	– 7.0835× 10^{− 4}	– 7.4358× 10^{− 4}	– 7.0879× 10^{− 4}
23– 19	5.8882× 10^{− 3}	5.8019× 10^{− 3}	5.8904× 10^{− 3}	5.8035× 10^{− 3}	23– 18	– 9.0212× 10^{− 4}	– 8.7207× 10^{− 4}	– 9.0296× 10^{− 4}	– 8.7254× 10^{− 4}
24– 20	6.7151× 10^{− 3}	6.6104× 10^{− 3}	6.7176× 10^{− 3}	6.6120× 10^{− 3}	24– 19	– 1.0852× 10^{− 3}	– 1.0631× 10^{− 3}	– 1.0862× 10^{− 3}	– 1.0635× 10^{− 3}
25– 21	7.6080× 10^{− 3}	7.4927× 10^{− 3}	7.6107× 10^{− 3}	7.4943× 10^{− 3}	25– 20	– 1.3069× 10^{− 3}	– 1.2842× 10^{− 3}	– 1.3082× 10^{− 3}	– 1.2845× 10^{− 3}
26– 22	8.5716× 10^{− 3}	8.4526× 10^{− 3}	8.5743× 10^{− 3}	8.4542× 10^{− 3}	26– 21	– 1.5711× 10^{− 3}	– 1.5382× 10^{− 3}	– 1.5725× 10^{− 3}	– 1.5385× 10^{− 3}
27– 23	9.6142× 10^{− 3}	9.4936× 10^{− 3}	9.6167× 10^{− 3}	9.4953× 10^{− 3}	27– 22	– 1.8730× 10^{− 3}	– 1.8282× 10^{− 3}	– 1.8744× 10^{− 3}	– 1.8285× 10^{− 3}

Table 4. Vibrational dipole moments μ _{υ ′ , υ ″} (Debye) computed by combining the ab initio potential and the ab initio electric dipole moments for the ground state CO.

Finally, the Herman– Wallis factors of CO calculated using the present unweighted fitted EDMF and aV6Z ACPF-field EDMF are compared with the measurements of Ogilvie et al. for the bands υ ′ – 0 (υ ′ = 1– 4) and the calculation of Chung et al. for the band 5– 0 in Fig. 2. The results are in good agreement with those presented by Ogilvie et al.^[19] and Chung et al.^[20] All results for the Δ = 1– 5 bands show that centrifugal distortion has only a minor influence on line intensities of the fundamental band but can be substantial in overtone transitions. The effect of centrifugal distortion on intensities increases with increasing Δ υ . The Herman– Wallis factor for the 5– 0 transition has a qualitatively different shape from and a larger magnitude than that of the lower overtones. It also clearly indicates that the intensities of the 5– 0 band in branch P are greater than those of the corresponding branch R lines. Chung et al. argued that several factors are responsible for such a condition, including the mutual interactions between higher-order terms of mechanical and electrical anharmonicities.^[20] Although the Herman– Wallis factors of the bands 1– 0, 2– 0, and 3– 0 calculated using the EDMF of Langhoff et al. agree with the measurements and calculations, the EDMFs of the bands 4– 0 and 5– 0, illustrated in Fig. 2 disagree with the experimental nor calculated results.^[36] This indicates that the present ab initio calculated EDMF is relatively accurate and may be adequate to evaluate line intensities.

	Figure Option View Download New Window
	Fig. 2. Herman– Wallis factors: ^{a, b} for bands υ ′ – 0 (υ ′ = 1– 5), ^cfor bands υ ′ – 0 (υ ′ = 1– 4), ^dfor band 5– 0, and ^efor bands 4– 0 and 5– 0.

3.4. Calculations and comparisons of line intensities

By combining the RKR potential, the EDMFs from the present weighted fits, and the aV6Z ACPF-field calculations, we calculate the rovibrational matrix moments that are used to compute the line intensities for the υ ′ – 0 (υ ′ = 1– 5) bands, in units of cm/mol at 296 K. The line intensities are then compared with the most current HITRAN (2012) database and measurements of the fundamental band and overtone bands up to υ ′ = 5.^[2] The results of the comparisons are plotted in Figs. 3– 7.

In Fig. 3, the calculated line intensities for the 1– 0 band of CO (X¹Σ ⁺) are compared using measurements from Zou et al.^[7] and the HITRAN database. The line intensities calculated using the present unweighted fitted EDMF are in better agreement with the experimental results of Zou et al.^[7] than the intensities in HITRAN. At − 23 ≤ m ≤ 25, the discrepancies in line intensities between the fitted EDMF and the experimental results of Zou et al. are estimated to be − 2.36%∼ 2.65%, while the discrepancies from the HITRAN comparison with the experimental results range from − 0.38 to − 5.38. The intensities in the HITRAN database are typically lower than the measurements given by Zou et al. The line intensities calculated using the aV6Z ACPF-field EDMF are somewhat larger than the ones of this fitted calculation, the HITRAN database, and Zou et al. Their discrepancies with the measurements are about 1.12%∼ 6.38, which indicates that our ab initio results are also acceptable. For the 1– 0 band, the band strengths calculated using the unweighted fitted and aV6Z ACPF-field EDMFs are 1.027× 10^{− 17} cm/mol and 1.061× 10^{− 17} cm/mol, respectively. These values agree well with the value of 1.022± 0.036× 10^{− 17} cm/mol derived by Varanasi and Sarangi and other data.^{[4, 6, 7, 10]}

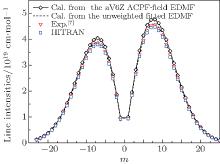	Figure Option View Download New Window
	Fig. 3. Comparisons of the present calculated line intensities with the measurements and the HITRAN database for the band 1– 0 of the CO.

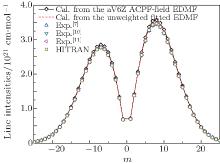	Figure Option View Download New Window
	Fig. 4. Comparisons of the present calculated line intensities with the measurements and the HITRAN database for the band 2– 0 of the CO.

Figure 4 illustrates the comparison for the 2– 0 band. The results show that the line intensities of the unweighted fit agree well with the HITRAN database and the experimental line intensities of Zou et al. and Devi et al.^{[2, 7, 10, 11]} The line intensities from the aV6Z field EDMF are slightly larger than the measurements of Zou et al. and Devi et al., ^{[7, 10, 11]} and their discrepancies are typically within ± 3. The band strengths that are obtained from the unweighted fitted and aV6Z ACPF-field EDMFs are 7.649× 10^{− 20} cm/mol and 7.768× 10^{− 20} cm/mol. Both agree well with the value of 7.466± 0.002× 10^{− 20} cm/mol computed using a fitted vibrational matrix moment and the experimental value of 7.532± 0.066× 10^{− 20} cm/mol.^{[7, 41]}

The measurements for the 3– 0 band given in Refs. [2], [13]– [15], and [17] are compared with the measurements made in this work and with those in the HITRAN database as shown in Fig. 5. The line intensities from the present study and HITRAN database^[2] are consistent with the 3– 0 band measurements presented in the literature. While the results of the unweighted fitted EDMFs and the aV6Z ACPF-field EDMFs are within 1% in agreement with the values provided by Chackerian et al.^[15] and Sung et al., ^[17] and the line intensities in the HITRAN ^[2] database correspond more closely to those of Henningsen et al.^[13] and Picqué et al.^[14]

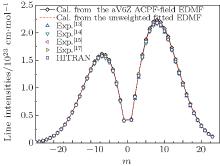	Figure Option View Download New Window
	Fig. 5. Comparisons of the present calculated line intensities with the measurements and the HITRAN database for the band 3– 0 of the CO.

Though Ogilvie et al. measured the strengths of lines for vibration– rotational bands of ¹²C¹⁶O, including the 4– 0 band, the parameters of the line intensities are not listed in their paper.^[19] Therefore, only the early experimental data of Chackerian and Valero^[18] are used for fits and comparison. These measurements as shown in Fig. 6, are compared with the calculated line intensities of the 4– 0 band and the corresponding values in the HITRAN database.^[2] The line intensities of the P and R branches as determined with the unweighted fit, are consistent with the referenced experimental results. Furthermore, the line intensities of the aV6Z field EDMF of the P branch are in better agreement with the experimental results than those of the R branch. In contrast, the line intensities from the HITRAN database match better with the measurements in the R branch.^[2] However, the values from the unweighted fitted EDMF, the aV6Z ACPF-field EDMF, and HITRAN do not agree with the experimental results when considering the intensities of the P(15), R(20), and R(23) lines. The discrepancy of the R(23) line exceeds 20%, and it may arise from the large error of the measurement. Still, values from the two EDMFs and HITRAN^[2] are consistent with each other.

The line intensity measurements for the 5– 0 overtone band are only performed by Chung et al. who merely presented 16 lines of the P branch with an overly high reported uncertainty.^[20] The minimum uncertainty of the line strength is likely to be 15%. The comparisons of line intensities for the 5– 0 band appear in Fig. 7. There are rather large discrepancies between the measurements and calculations of Chung et al., i.e., the line intensities of the unweighted fit and of the aV6Z ACPF-field EDMF.^[20] The unweighted fit line intensities agree better with the results using the aV6Z ACPF-field EDMF. The calculated results again show that the line intensities in branch P are truly greater than those in branch R. For the 5– 0 band, the band strengths obtained from the weighted fitted and aV6Z ACPF-field EDMFs are 5.585× 10^{− 27} cm/mol and 5.674× 10^{− 27} cm/mol, which are in close agreement with the experimental results of 5.1± 1.3× 10^{− 27} cm/mol.^[20] Considering the rather large experimental uncertainties, we argue that the present intensities of the unweighted fitted line and the aV6Z ACPF-field EDMFs are still reliable and reflect the basic qualitative characteristics of spectral lines.

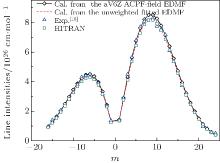	Figure Option View Download New Window
	Fig. 6. Comparisons of the present calculated line intensities with the measurements and the HITRAN database for the band 4– 0 of the CO.

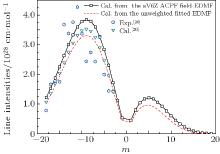	Figure Option View Download New Window
	Fig. 7. Comparisons of the line intensities of the CO 5– 0 band with the measurements and the calculations of Chung et al.^[20]

The comparisons of line intensity, presented here, between the values from the HITRAN database and experimental measurements clearly show that the EDMF can be directly constructed from the experimental rovibrational transition matrix elements and can provide accurate values for CO (X¹Σ ⁺). Although the line intensities calculated using the aV6Z ACPF-field EDMF are greater than the measurements at the υ ′ – 0 (υ ′ = 1– 5) band, the discrepancies are within the admissible range of deviation between theoretical calculation and measurement.

4. Conclusions

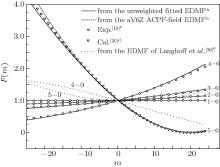
By using a weighted and unweighted approach to fit the best available data of individual rovibrational transitions of CO (X¹Σ ⁺), we obtain an accurate EDMF within the valid range of 0.967 Å ≤ r ≤ 1.322 Å , which agrees well with that of Chung et al.^[20] Meanwhile, an accurate ab initio EDMF is also calculated at the ACPF/aug-cc-pV6Z level with a finite-field of ± 0.005 a.u. The fitted EDMF in the valid range shows close agreement with the ab initio EDMF, and for small values of r, the electric dipole moment values are slightly smaller than the previous theoretical results of Langhoff and Bauschlicher.^[36] Combining the RKR potential curve and these EDMFs, the transition matrix moments are computed and compared with the experimental ones. The vibrational transition matrix moments μ _{υ ′ , υ ″} calculated by using our unweighted fitted EDMF are in excellent agreement with the experimental values. The Herman– Wallis factors calculated using the present aV6Z ACPF-field EDMF also agree well with the experimental measurements. Comparisons are made among line intensities calculated here, reported in the HITRAN^[2] database and obtained from experimental measurements. The results clearly show that the present unweighted fitted and aV6Z ACPF-field EDMFs are accurate and useful in predicting the spectral properties of the CO molecule.

Reference

View Option

1	Winnewisser G, Herbst E and Ungerechts H 1992 Spectroscopy of the Earth’s atmosphere and interstellar mediu Boston Academic Press [Cited within:1]
2	Rothman L S, Gordon I E, Babikov Y, Barbe A, Chris Benner D, Bernath P F, Birk M, Bizzocchi L, Boudon V, Brown L R, Campargue A, Chance K, Cohen E A, Coudert L H, Devi V M, Drouin B J, Fayt A, Flaud J M, Gamache R R, Harrison J J, Hartmann J M, Hill C, Hodges J T, Jacquemart D, Jolly A, Lamouroux J, LeRoy R J, Li G, Long D A, Lyulin O, Mackie C, Massie S T, Mikhailenko S, Müller H S, Naumenko O, Nikitin A, Orphal J, Perevalov V I, Perrin A, Polovtseva E R, Richard C, Smith M A H, Starikova E, Sung K, Tashkun S, Tennyson J, Toon G C, Tyuterev Vl G and Wagner G 2013 J. Quantum Spectrosc. Radiat. Transfer 130 4 DOI:10.1016/j.jqsrt.2013.07.002 [Cited within:10]
3	Rothman L S, Gordon I E, Barberb R J, Dothe H, Gamache R R, Goldman A, Perevalov V I, Tashkun S A and Tennyson J 2010 J. Quantum Spectrosc. Radiat. Transfer 111 2139 DOI:10.1016/j.jqsrt.2010.05.001 [Cited within:1]
4	Varansi P and Sarangi S 1975 J. Quantum Spectrosc. Radiat. Transfer 15 473 DOI:10.1016/0022-4073(75)90066-7 [Cited within:2]
5	Varghese P L and Hanson R K 1980 J. Quantum Spectrosc. Radiat. Transfer 24 479 DOI:10.1016/0022-4073(80)90017-5 [Cited within:1]
6	Chackerian Jr C, Guelachvili G and Tipping R H 1983 J. Quantum Spectrosc. Radiat. Transfer 30 107 DOI:10.1016/0022-4073(83)90091-2 [Cited within:2]
7	Zou Q and Varanasi P 2002 J. Quantum Spectrosc. Radiat. Transfer 75 63 DOI:10.1016/S0022-4073(02)00007-9 [Cited within:9]
8	Bouanich J P and Brodbeck C 1974 J. Quantum Spectrosc. Radiat. Transfer 14 1199 DOI:10.1016/0022-4073(74)90090-9 [Cited within:2]
9	Chand raiah G and Hébert G R 1981 Can. J. Phys. 59 1367 DOI:10.1139/p81-179 [Cited within:1]
10	Devi V M, Benner D C, Smith M A H, Rinsland C P and Mantz A W 2002 J. Quantum Spectrosc. Radiat. Transfer 75 455 DOI:10.1016/S0022-4073(02)00023-7 [Cited within:3]
11	Devi V M, Benner D C, Smith M A H, Mantz A W, Sung K, Brown L R and Predoi-Cross A 2012 J. Quantum Spectrosc. Radiat. Transfer 113 1013 DOI:10.1016/j.jqsrt.2012.02.010 [Cited within:3]
12	Toth R A, Hunt R H and Plyler E K 1969 J. Mol. Spectrosc. 32 85 DOI:10.1016/0022-2852(69)90144-1 [Cited within:2]
13	Henningsen J, Simonsen H, M?gelberg T and Truds? E 1999 J. Mol. Spectrosc. 193 354 DOI:10.1006/jmsp.1998.7735 [Cited within:2]
14	Picqué N, Guelachvili G, Dana V and Mand in J Y 2000 J. Mol. Spectrosc. 517–518 427 DOI:10.1016/S0022-2860(99)00267-7 [Cited within:1]
15	Chackerian C Jr, Freedman R, Giver L P and Brown L R 2001 J. Mol. Spectrosc. 210 119 DOI:10.1006/jmsp.2001.8447 [Cited within:2]
16	Jacquemart D, Mand in J Y, Dana V, Picqué N and Guelachvili G 2001 Eur. Phys. J. D 14 55 DOI:10.1007/s100530170235 [Cited within:1]
17	Sung K and Varanasi P 2004 J. Quantum Spectrosc. Radiat. Transfer 83 445 DOI:10.1016/S0022-4073(03)00015-3 [Cited within:4]
18	Chackerian C Jr and Valero Francisco P J 1976 J. Mol. Spectrosc. 62 338 DOI:10.1016/0022-2852(76)90274-5 [Cited within:3]
19	Ogilvie J F, Cheah S L, Lee Y P and Sauer S P A 2002 Theor. Chem. Acc. 108 85 DOI:10.1007/s00214-002-0337-y [Cited within:7]
20	Chung C Y, Ogilvie J F and Lee Y P 2005 J. Phys. Chem. A 109 7854 DOI:10.1021/jp052035x [Cited within:14]
21	Chackerian C Jr 1976 J. Chem. Phys. 65 4228 DOI:10.1063/1.432830 [Cited within:1]
22	Chackerian C Jr and Tipping R H 1983 J. Mol. Spectrosc. 99 431 DOI:10.1016/0022-2852(83)90324-7 [Cited within:1]
23	Bouanich J P, Thanh N V and Rossi I 1983 J. Quantum Spectrosc. Radiat. Transfer 30 9 DOI:10.1016/0022-4073(83)90067-5 [Cited within:1]
24	Chackerian C Jr, Fakkenq R, Guelachvili G, Rossetti C and Urba W 1984 Can. J. Phys. 62 1579 DOI:10.1139/p84-202 [Cited within:1]
25	Kiriyama F and Rao B S 2000 J. Quantum Spectrosc. Radiat. Transfer 65 673 DOI:10.1016/S0022-4073(99)00138-7 [Cited within:1]
26	Buldakov M A and Cherepanov V N 2004 J. Phys. B: At. Mol. Opt. Phys. 37 3973 DOI:10.1088/0953-4075/37/19/015 [Cited within:1]
27	Goorvitch D and Chackerian C JR 1994 Astrophys. J. Suppl. Ser. 91 483 DOI:10.1086/191945 [Cited within:1]
28	Goorvitch D and Chackerian C JR 1994 Astrophys. J. Suppl. Ser. 92 311 DOI:10.1086/191970 [Cited within:1]
29	Goorvitch D 1994 Astrophys. J. Suppl. Ser. 95 535 DOI:10.1086/192110 [Cited within:1]
30	Young L A and Eachus W J 1966 J. Chem. Phys. 44 4195 DOI:10.1063/1.1726605 [Cited within:1]
31	Werner H J 1981 Mol. Phys. 44 111 DOI:10.1080/00268978100102311 [Cited within:1]
32	Cooper D M and anghoff S R 1981 J. Chem. Phys. 74 1200 DOI:10.1063/1.441227 [Cited within:1]
33	Diercksen G H F and Sadlej A 1985 Chem. Phys. 96 17 DOI:10.1016/0301-0104(85)80193-2 [Cited within:1]
34	Diercksen G H F and Sadlej A 1985 Chem. Phys. 96 43 DOI:10.1016/0301-0104(85)80194-4 [Cited within:1]
35	Kellö V, Noga J, Dierchsen G H F and Sadlej A 1988 Chem. Phys. Lett. 152 387 DOI:10.1016/0009-2614(88)80111-8 [Cited within:1]
36	Langhoff S R and Bauschlicher Jr C W 1995 J. Chem. Phys. 102 5220 DOI:10.1063/1.469247 [Cited within:6]
37	Schautz F and Flad H J 1999 J. Chem. Phys. 110 11700 DOI:10.1063/1.479170 [Cited within:1]
38	Tipping R H and Herman R M 1970 J. Mol. Spectrosc. 36 404 DOI:10.1016/0022-2852(70)90217-1 [Cited within:1]
39	Kiriyama F, Rao B S and Nangia V K 2001 J. Quantum Spectrosc. Radiat. Transfer 69 35 DOI:10.1016/S0022-4073(00)00059-5 [Cited within:1]
40	Li G, Gordon I E, Bernath P F and Rothman L S 2011 J. Quantum Spectrosc. Radiat. Transfer 112 1543 DOI:10.1016/j.jqsrt.2011.03.014 [Cited within:1]
41	Brault J W, Brown L R, Chackerian C Jr, Freedman R, Predoi-Cross A and Pin A S 2003 J. Mol. Spectrosc. 222 220 DOI:10.1016/j.jms.2003.07.002 [Cited within:2]
42	Knowles P J and Werner H J 1985 Chem. Phys. Lett. 115 259 DOI:10.1016/0009-2614(85)80025-7 [Cited within:1]
43	Gdanitz R J and Ahlrichs R 1988 Chem. Phys. Lett. 143 413 DOI:10.1016/0009-2614(88)87388-3 [Cited within:1]
44	Werner H J, Knowles P J, Knizia G, Manby F R and Schütz Met al. MOLPRO version 2009. 1, a package of ab initio programs, 2009, see http://www.molpro.net. [Cited within:1]
45	Peterson K A, Woon D E and Dunning T H 1994 J. Chem. Phys. 100 7410 DOI:10.1063/1.466884 [Cited within:1]
46	Peterson K A, Kendall R A and Dunning T H 1993 J. Chem. Phys. 99 1930 DOI:10.1063/1.465307 [Cited within:1]
47	Dunning T H 1989 J. Chem. Phys. 90 1007 DOI:10.1063/1.456153 [Cited within:1]
48	[Cited within:2]
49	[Cited within:1]
50	Velichko T I, Mikhailenko S N and Tashkun S A 2012 J. Quantum Spectrosc. Radiat. Transfer 113 1643 DOI:10.1016/j.jqsrt.2012.04.014 [Cited within:1]
51	Le Roy R J A Practical Guide to Least-Squares Fitted, University of Waterloo Chemical Physics Research Report CP-628; 1997see: <http://scienide2.uwaterloo.ca/simrleroy/?tting/> [Cited within:1]
52	Huber K P and Herzberg G 1979 Constants of Diatomic Molecules New York Van Nostrand Reinhold [Cited within:1]
53	Chackerian C, Kshirsagar R J, Giver L P and Brown L R 1999 OSA Tech. Dig. (1999 Opt. Soc. Am. ) 22 139 DOI:10.1364/FTS.1999.FWE22 [Cited within:1]

1992

0.0

... ^[1] The spectral parameters of CO are included in well-known spectroscopic databases such as the high-resolution transmission (HITRAN) molecular database,^[2] the high-temperature version of HITRAN called the HITEMP database,^[3] and others ...

2013

0.0

... ^[2] The results of the comparisons are plotted in Figs ...

... ^[2,7,10,11] The line intensities from the aV6Z field EDMF are slightly larger than the measurements of Zou et al ...

... [2], [13]#cod#x2013 ...

... The line intensities from the present study and HITRAN database^[2] are consistent with the 3#cod#x2013 ...

... ,^[17] and the line intensities in the HITRAN ^[2] database correspond more closely to those of Henningsen et al ...

... ^[2] The line intensities of the P and R branches as determined with the unweighted fit, are consistent with the referenced experimental results ...

... ^[2] However, the values from the unweighted fitted EDMF, the aV6Z ACPF-field EDMF, and HITRAN do not agree with the experimental results when considering the intensities of the P(15), R(20), and R(23) lines ...

... Still, values from the two EDMFs and HITRAN^[2] are consistent with each other ...

... Comparisons are made among line intensities calculated here, reported in the HITRAN^[2] database and obtained from experimental measurements ...

2010

0.0

1975

0.0

... 0,^{[4#cod#x2013 ...}

... ^[4,6,7,10] ...

1980

0.0

1983

0.0

... ^[6] is also included in the fitting work ...

... ^[4,6,7,10] ...

2002

0.0

... 7] the first overtone 2#cod#x2013 ...

... 0,^{[7#cod#x2013 ...}

... ^[7] for the fundamental band, Brulat et al ...

... ^[7] and the HITRAN database ...

... ^[7] than the intensities in HITRAN ...

... ^[4,6,7,10] ...

... ^[2,7,10,11] The line intensities from the aV6Z field EDMF are slightly larger than the measurements of Zou et al ...

... ,^[7,10,11] and their discrepancies are typically within #cod#x00B1 ...

... ^[7,41] ...

1974

0.0

... ^{[8,12#cod#x2013 ...}

... ^{[8,12,19,21#cod#x2013 ...}

1981

0.0

2002

0.0

... ^[4,6,7,10] ...

... ^[2,7,10,11] The line intensities from the aV6Z field EDMF are slightly larger than the measurements of Zou et al ...

... ,^[7,10,11] and their discrepancies are typically within #cod#x00B1 ...

2012

0.0

... 11] and the second overtone 3#cod#x2013 ...

... ^[2,7,10,11] The line intensities from the aV6Z field EDMF are slightly larger than the measurements of Zou et al ...

... ,^[7,10,11] and their discrepancies are typically within #cod#x00B1 ...

1969

0.0

... ^{[8,12#cod#x2013 ...}

... ^{[8,12,19,21#cod#x2013 ...}

1999

0.0

... [2], [13]#cod#x2013 ...

... ^[13] and Picqu#cod#x00E9 ...

2000

0.0

... ^[14] ...

2001

0.0

... [15], and [17] are compared with the measurements made in this work and with those in the HITRAN database as shown in Fig ...

... ^[15] and Sung et al ...

2001

0.0

2004

0.0

... 17] Many studies in the past decade have focused on the 3#cod#x2013 ...

... s^[17] for the 3#cod#x2013 ...

... [15], and [17] are compared with the measurements made in this work and with those in the HITRAN database as shown in Fig ...

... ,^[17] and the line intensities in the HITRAN ^[2] database correspond more closely to those of Henningsen et al ...

1976

0.0

... Chackerian and Valero^[18] measured the absolute rovibrational intensities of the 4#cod#x2013 ...

... s^[18] for the 4#cod#x2013 ...

... ^[19] Therefore, only the early experimental data of Chackerian and Valero^[18] are used for fits and comparison ...

2002

0.0

... ^[19] have evaluated the electric dipolar moments based on new experimental measurements of line strengths including the 4#cod#x2013 ...

... ^{[8,12,19,21#cod#x2013 ...}

... ^{[19,30#cod#x2013 ...}

... ^[19] through using the MCSCF method are all plotted in Fig ...

... ^[19] disagrees with the three fitted and the two theoretical ones ...

... ^[19] and Chung et al ...

... ^[19] Therefore, only the early experimental data of Chackerian and Valero^[18] are used for fits and comparison ...

2005

0.0

... ^[20] adapted a cavity ringdown spectral technique in the near-infrared region to measure the 5#cod#x2013 ...

... ^[20] A considerable number of quantum chemical calculations of EDMFs for CO have been presented in various papers ...

... s^[20] for the 5#cod#x2013 ...

... ^[20] Table#cod#x00A0 ...

... ^[20] Meanwhile, the theoretical EDMFs calculated through using the ACPF method at the aV6Z set level with the field values of #cod#x00B1 ...

... ^[20] The valid range of the fitted EDMF is controlled by the largest overtones which are very sensitive to determining the higher coefficients of M_i in Eq ...

... ,^[20] and Langhoff and Bauschlicher,^[36] and the present fits, we calculate the rovibrational matrix moments and vibrational matrix moments ...

... ^[20] Thus, only the unweighted fitted EDMF will be considered when comparing line intensities later in the article ...

... ^[20] All results for the #cod#x0394 ...

... ^[20] Although the Herman#cod#x2013 ...

... ^[20] The minimum uncertainty of the line strength is likely to be 15% ...

... ^[20] The unweighted fit line intensities agree better with the results using the aV6Z ACPF-field EDMF ...

... ^[20] Considering the rather large experimental uncertainties, we argue that the present intensities of the unweighted fitted line and the aV6Z ACPF-field EDMFs are still reliable and reflect the basic qualitative characteristics of spectral lines ...

... ^[20] Meanwhile, an accurate ab initio EDMF is also calculated at the ACPF/aug-cc-pV6Z level with a finite-field of #cod#x00B1 ...

1976

0.0

... ^{[8,12,19,21#cod#x2013 ...}

1983

0.0

... 26] For instance, based on the inversion of experimental intensity information, Chackerian and Tipping^[22] derived a hybrid EDMF in a Pad#cod#x00E9 ...

1983

0.0

1984

0.0

2000

0.0

2004

0.0

... 26] For instance, based on the inversion of experimental intensity information, Chackerian and Tipping^[22] derived a hybrid EDMF in a Pad#cod#x00E9 ...

1994

0.0

... ^[27,28,29] In consideration of these pure vibrational matrix elements of the bands #cod#x03C5 ...

1994

0.0

... ^[27,28,29] In consideration of these pure vibrational matrix elements of the bands #cod#x03C5 ...

1994

0.0

... ^[27,28,29] In consideration of these pure vibrational matrix elements of the bands #cod#x03C5 ...

1966

0.0

... ^{[19,30#cod#x2013 ...}

1981

0.0

1981

0.0

1985

0.0

1985

0.0

1988

0.0

1995

0.0

... , those by Langhoff and Bauschlicher^[36] through using the aug-cc-pVQZ ACPF-field method, and those by Ogilvie et al ...

... ^[36] The three lines outside the valid range are not consistent with the two theoretical EDMFs at large internuclear distances ...

... Compared with the theoretical results given by Langhoff and Bauschlicher,^[36] the values of the dipole moments are smaller at small r and slightly larger at large r ...

... ,^[20] and Langhoff and Bauschlicher,^[36] and the present fits, we calculate the rovibrational matrix moments and vibrational matrix moments ...

... ^[36] This indicates that the present ab initio calculated EDMF is relatively accurate and may be adequate to evaluate line intensities ...

... ^[36] Combining the RKR potential curve and these EDMFs, the transition matrix moments are computed and compared with the experimental ones ...

1999

0.0

... 37] However, we find that the vibrational transition matrix elements (or rotationless transition matrix elements) calculated using the quantum chemical EDMFs along with the Rydberg#cod#x2013 ...

1970

0.0

... ^[38] The single and double primes correspond to the upper and lower states, respectively ...

2001

0.0

... ^[39,40] In order to derive the new EDMF from Eq ...

2011

0.0

... ^[39,40] In order to derive the new EDMF from Eq ...

2003

0.0

... s^[41] for the first overtone band, Sung et al ...

... ^[7,41] ...

1985

0.0

... We compute the EDMF by using highly correlated ab initio methods, namely, the complete active space self-consistent field (CASSCF)^[42] approach followed by the highly accurate averaged coupled-pair functional (ACPF)^[43] method in the C_2V point group ...

1988

0.0

... 1 program package,^[44] with and without a finite-field approach with field values of #cod#x00B1 ...

1994

0.0

... ^{[45#cod#x2013 ...}

1993

0.0

1989

0.0

... 47] These basis sets are sufficiently diffuse to describe long-range interactions so that a more accurate EDMF can be determined at larger internuclear separations ...

2007

0.0

... 0 program,^[48] the piecewise polynomial interpolation is performed by using numerical input potential energies and electric dipole moments ...

... ^[48] The rovibrational matrix elements are then evaluated from the measured line intensities according to ...

0.0

... ^[49,50] ...

2012

0.0

... ^[49,50] ...

1997

0.0

... ^[51] Six coefficients of the EDMF, M₀, M₁, M₂,#cod#x2026 ...

1979

0.0

... ^[52] The calculated energies and dipole moments each as a function of r are listed in Table#cod#x00A0 ...

1999

0.0