In nervous systems, neurons’ encoding, transferring, and integrating information are realized by a series of action potentials. Action potentials play a big role in nervous systems. The Hindmarsh– Rose (HR) model is a well-known model that describes the action potentials generated by HR neurons. During the past few decades, scholars from different fields of science, such as biology, physics, neuroscience, mathematics, computer science, and electronics, have paid a great deal of attention to researching the HR neuron model. In such a kind of research activity, it is common to take experimental studies.^{[1, 2]} Additionally, the HR neuron model is also acquired experimentally. However, for the study of animal and human nervous systems, numerical simulations and other hardware implementations of neurons and neuron networks are also commonly used approaches.

In general, simulation is an easy and effective approach. Numerical simulations are often performed before experimental implementation. For instance, in order to analyze the chaotic motion and realize the control or synchronization of neurons and neural networks, simulations are performed first.^{[3– 7]} Impulsive control and synchronization of a chaotic HR neuron model are studied in Ref.  [3], and the research results are helpful to understand the dynamical mechanism of signal encoding and transduction from information processing of neuronal activities. Dynamics of a single HR neuron and a neural network-based sliding mode controller is proposed to synchronize the master HR neuron and the slave HR neuron in Ref.  [4]. An H_∞ controller via adaptive neural networks is designed to synchronize two Ghostburster neurons in Ref.  [5]. Adaptive control approaches, ^[6] an exponentially fast synchronization approach, ^[7] and an observer-based synchronization approach^[8] are also developed to realize the synchronization of two HR neurons. Such simulation results are beneficial to experiments.

However, computer simulations have a finite precision, and experimental measurements also have finite ranges (both in time and frequency domains). The behaviors of neurons witnessed might be an artifact of the observation devices, or the behaviors might actually be regular but with a period or bandwidth beyond the limits capturable by devices. In fact, cases have arisen in which supposed chaotic behavior turned out to be a periodic orbit with a very long period. With an attempt to solve this uncertainty, an analytical approach is of necessity which guarantees that the chaotic behavior does exist. One of the most useful tools for autonomous systems is the work of Shil’ nikov (see Ref.  [9] and the references therein). With the help of the Shil’ nikov theorem, the chaotic properties of mechanically and electrically coupled nonlinear dynamical systems have been discussed. A rigorous proof of the existence of Shil’ nikov-sense Smale horseshoe chaos has been presented. Conditions which lead to chaos have been obtained in Ref.  [10]. A new kind of piecewise linear chaotic system with multi-scrolls, ^[11] the existence of a chaotic attractor for triangular systems with quadratic form, ^[12] and new three-dimensional square chaotic systems^{[13– 16]} have been discussed and constructed based on the Shil’ nikov theorem.

In the present paper, we will focus on the chaotic analysis of HR neurons by the Shil’ nikov method. The chaotic threshold of external current stimulus will be obtained. At the same time, the homoclinic orbit of HR neurons is also acquired by series solution to differential equations.

The rest of the paper is organized as follows. The HR neuron model is presented in Section 2. The chaotic analysis by the Shil’ nikov technique is performed in Section 3. Section 4 focuses on the numerical simulation results, which are utilized to support the theoretical analysis. In the end, conclusions are drawn in Section 5.

The HR neuron model can be described as^{[3, 4]}

where x is the membrane potential, y is a recovery variable associated with the fast current of Na⁺ or K⁺ ions, and z is adaptation current associated with the slow current of a Ca^{2 +} ion. Here, a = 1, b = 3, c = 1, d = 5, s = 4, r = 0.006, x₀ = − 1.6, and I_ext is the external current input.

The equilibrium  point is

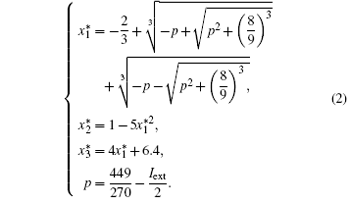
Taking the following coordinate transformation:

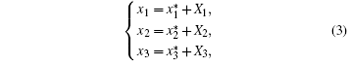
system  (1) can be rewritten as

The equilibrium point of system  (4) is (0, 0, 0)^T.

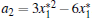
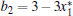
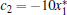
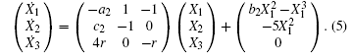
Let , , , then system (4) can be rewritten as

In this section, we focus on the chaos analysis of the HR neuron model. One of the most important tools for analyzing chaotic behaviors of nonlinear dynamical systems is the Shil’ nikov theorem. We will take it as a lemma to analyze the condition of external current stimulus in producing chaotic behaviors of HR neurons.

Lemma 1 (Shil’ nikov theorem^[17]) For a three-dimensional autonomous system

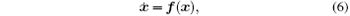
where x ∈ R³, f : R³ ↦ R³ belongs to C^r(r ≥ 2). Let x₀ be an equilibrium point of system  (6), and J = Df(x₀) is a Jacobian matrix at x₀. The eigenvalues of the Jacobian matrix J are in the form of

If | γ | > | σ | , and there exists a homoclinic orbit Γ based at x₀, then system (6) has Smale horseshoe-type chaos.

Theorem 1 System (5) has Smale horseshoe-type chaos, if external current stimulus I_ext satisfies the inequality 2.9 < I_ext < 3.5.

Proof For system (5), the Jacobian matrix at equilibrium point (0, 0, 0)^T is

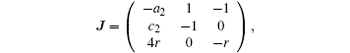
then the characteristic equation is

If we let λ = θ − (1 + r + a₂)/3, then equation  (7) can be rewritten as

where

According to the Cardano foumular, if

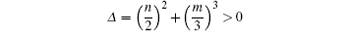
and

then, for Eq.  (8), there are three eigenvalue γ , σ ± jω , and γ < 0, σ > 0, | γ | > | σ | .

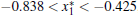
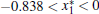
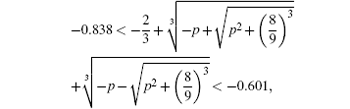
Hence, we have , i.e., . According to Eq.  (2), we have

therefore

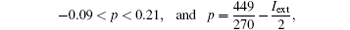
hence

Next, we will try to find the homoclinic orbit of HR neurons. A series solution to system  (5) will be discussed.

When t ≥ 0, let X₁ (t), X₂ (t), X₃ (t) be

where A_k, B_k, and C_k are parameters which need to be determined; α is the negative eigenvalue. Supposing that equation  (10) is the series solution to system (5), equations  (11)– (13) will be obtained when we substitute Eq.  (10) into Eq.  (5).

For k= 1

Since det(α E − J) = 0, and (A₁, B₁, C₁)^T ≠ (0, 0, 0)^T, A₁, B₁, and C₁ can be determined by arbitrary parameters ξ .

Similarly, the following equations will be obtained, for k = 2,

for k > 2

where m + n + p = k, τ ₁ + τ ₂ + τ ₃ = 3, and

Since det(kα E − J) ≠ 0, k > 1, A_k, B_k, C_k, (k > 1) can be calculated as follows: for k= 2

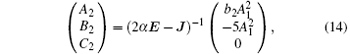
for k > 2

So far, when t > 0, the series solution to system (5) has been acquired.

For t < 0, let τ = − t(t > 0), system (5) can be rewritten as

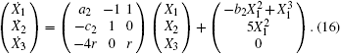
Similarly, let X₁(τ ), X₂(τ ), X₃(τ ) be

which are the series solution to system  (16). We may substitute Eq.  (17) into Eq.  (16), then when k = 1

for k = 2

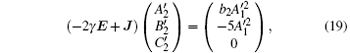
for k > 2

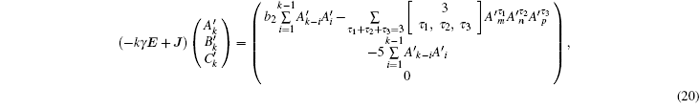
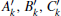
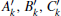
where , and γ are parameters we need to determine, and γ is negative. If we choose γ = α , then equation  (18) has a nontrivial solution , and can be determined by arbitrary parameters η . can be calculated as follows: for k = 2

for k > 2

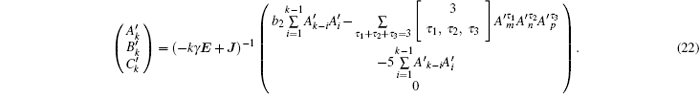
Therefore, the homoclinic orbit of system (5) can be written as

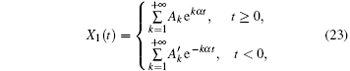
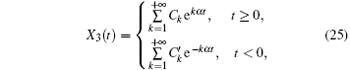
where ξ and η can be determined by

According to the Shil’ nikov theorem, system  (5) has Smale horseshoe-type chaos, i.e., the theorem has been proofed.

In order to verify the theoretical results deduced in Section 3, we will give the phase trajectories, time domain responses, and Lyapunov exponent spectra to show the chaotic behaviors of HR neurons. Parameters chosen in simulations are shown in Table  1.

Table 1.

Table 1.

Table 1. Parameters chosen in simulations. Parameters Values Parameters Values a 1 x0 – 1.6 b 3 Iext 3.2/2.5 c 1 x(0) 0 d 5 y(0) 0.05 s 4 z(0) 0.02 r 0.006

Table 1. Parameters chosen in simulations.

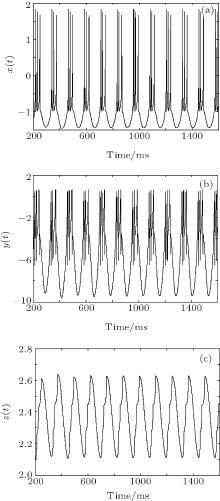
Figure  1 shows the time responses of the HR neurons, figure  2 displays the phase trajectories of HR neurons, and figure  3 depicts the dynamics of Lyapunov exponents. From Fig.  3, we can see clearly that one of the Lyapunov exponents is larger than zero, which means HR neurons’ action potentials are chaotic when the external current stimulus is chosen to be 3.2 (within the range defined by inequality  (9)).

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Time responses of HR neurons when Iext = 3.2.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Phase trajectories of HR neurons when Iext = 3.2.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Dynamics of Lyapunov exponents for HR neurons when Iext = 3.2.

However, when I_ext equals 2.5, which is not in the range defined by inequality (9), the action potentials of HR neurons are periodic. Figures  4 and 5 show the periodic time responses and periodic phase trajectories of HR neurons. Figure  6 describes the maximum Lyapunov exponents that are less than zero clearly.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Time responses of HR neurons when Iext = 2.5.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Phase trajectories of HR neurons when Iext = 2.5.

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. Dynamics of Lyapunov exponents for HR neurons when Iext = 2.5.

The range of external current stimulus generating chaotic behaviors of HR neurons is discussed in this paper. Based on the Shil’ nikov theorem, the external current conditions for chaotic HR neurons are obtained rigorously mathematically. The analytical approach to neurons’ chaotic behaviors guarantees that the chaotic action potentials of HR neurons do exist in a formal sense, which avoids the shortcomings of experimental and simulation approaches. The results also provide guidance for experimental and numerical simulation researches.