†Corresponding author. E-mail: xlin@nwpu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 51271213 and 51323008), the National Basic Research Program of China (Grant No. 2011CB610402), the National High Technology Research and Development Program of China (Grant No. 2013AA031103), the Specialized Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20116102110016), and the China Postdoctoral Science Foundation (Grant No. 2013M540771).
A quantitative cellular automaton model is used to study the cell-to-dendrite transition (CDT) in directional solidification. We give a detailed description of the CDT by carefully examining the influence of the physical parameters, including: the Gibbs–Thomson coefficient Γ, the solute diffusivity Dl, the solute partition coefficient k0, and the liquidus slope ml. It is found that most of the parameters agree with the Kurz and Fisher (KF) criterion, except for k0. The intrinsic relations among the critical velocity Vcd, the cellular primary spacing λc,max, and the critical spacing λcd are investigated.
The solidification microstructure determines the properties of the final product. The directional solidification of binary alloys can produce planar, cellular, and dendritic interfaces.[1– 12] The transition from planar to cellular interface can be well established by the Mullins– Sekerka instability theory.[1] When the growth velocity V exceeds a threshold value Vc, the planar interface transients into a steady state cellular microstructure of wavelength λ c. The depth of the cellular groove can be short, that is: shallow cell. A cellular groove can also be long, that is: deep cell. For even higher velocities, deep cells change into dendrites. The cell-to-dendrite transition (CDT) has been investigated for decades. However, the criterion of transition from a cellular to a dendritic microstructure has not been well established. Kurz and Fisher[2] have proposed that Vcd = Vc/k0 (Vcd = growth velocity of cellular– dendrite transition, Vc = planar growth stability limit, and k0 = solute partition coefficient). Trivedi[3] presented a minimum in the solute Peclet number p, which supported Kurz and Fisher (KF) criterion. Laxmanan et al.[4] concluded that the KF criterion was doubtful, except for succinonitrile-acetone (SCN-ace) and Al– 2% Cu alloys. Other alloys, such as SCN– Salol and Pb– Sn, did not support the KF criterion.
The onset of the sidewise instability has recently been investigated through the examination of the local spacing λ cd of the CDT by Georgelin and Pocheau, [8] and Trivedi et al.[9, 10] They found that cells and dendrites coexist over a range of velocities under fixed temperature gradient G and initial composition C0. Within the transition zone, a critical spacing λ cd is found, under which dendrites transform into cells and above which cells transform to dendrites. Georgelin and Pocheau[8] analyzed an expression of the critical side-branching spacing, that is 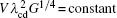
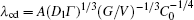
To obtain a deep understanding of the CDT, the accuracy of the expressions of λ c, max, λ d, min, and λ cd should be quantitatively examined to void incorrect formulas. The relationship among λ cd, G, V, and C0 has been quantitatively established by thin-film experiments. However, in experiments, the physical parameters, such as the Gibbs– Thomson coefficient Γ , the solute diffusivity Dl, the solute partition coefficient k0, and the liquidus slope ml, cannot be exhaustively surveyed. To quantitatively examine the influence of physical parameters on the CDT, numerical simulation is the only option. The phase-field model[13– 26] has a nontrivial computational challenge to survey this problem. In this paper, a quantitative cellular automaton (CA) model[32– 35] is used to investigate the influence of physical parameters on the CDT in directional solidification. In this paper, various CDT morphologies are simulated with different strengths of physical parameters while keeping the other parameters unchanged.
The computational domain is divided into a Cartesian grid. Each grid, which is also called a cell, is characterized by the following three states: liquid, solid, and interface, as seen in Fig. 1. To govern the transition of cell states, a capture rule is needed to control the evolution of different states. A solid fraction (i.e. solid cell fs = 1, liquid cell fs = 0, and interface cell 0 < fs < 1) is introduced to implicitly capture the solid– liquid interface. The growth of solid fractions can be calculated according to the interface kinetics, which is also based on the algorithms of the interface curvature calculation and the thermal or mass transport calculation. The thermal and mass transport calculation methods can be found elsewhere.[28– 30] The following subsections focus on the capture rule, interface curvature calculation, and the interface growth kinetics.
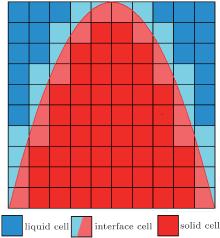 | Fig. 1. The scheme of solid– liquid interface in CA model: liquid cell, interface cell, and solid cell. |
During the CA simulation, the transition of the cell state from liquid to interface is governed by the capture rule. Since the transition of cell states influences the growth of solid– liquid interface, the capture rule used in the CA model should be carefully selected. The traditional capture rules, such as von Neumann’ s and Moore’ s rules, were evidenced to have strong artificial anisotropy.[28] The capture rule in the present CA model used a limited neighbor solid fraction (LNSF) method, [35] which is the modification of the von Neumann’ s rule.
Based on the von Neumann’ s rule, the LNSF method calculates the averaged solid fraction fsave around a specific liquid cell. If fsave is larger than a constant value fsconst, then the liquid cell can be captured by von Neumann’ s rule. Otherwise, if fsave is less than fsconst, then the liquid cell cannot be captured, even if it is satisfied by von Neumann’ s rule. The LNSF method was effective for the pure substance CA mode, [35] in which the artificial anisotropy could be reduced to a large extent. More importantly, the LNSF method is only based on some basic algebraic operators, which means that the LNSF method is as computationally efficient as von Neumann’ s rule. In the present work, the LNSF method was applied to the simulation of directional solidification.
The accuracy in curvature calculation has a significant influence on the accuracy of the CA model. As far as is known, the most popular method for the simulation of interface curvature is the counting cell method.[28]
However, the counting cells method is not accurate enough for quantitative simulation.[28] A more accurate method is based on the variation of the unit vector normal (VUVN) to the solid– liquid interface along the direction of the interface, [29]
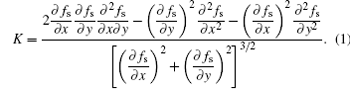
The VUVN method needs to calculate the derivatives of solid fraction, which are difficult to be precisely calculated in a sharp interface model. A bilinear interpolation method was used in the CA model, the detail of which can be found in Ref. [32].
The interface growth kinetics used in this paper are proposed by Zhu and Stefanescu as[29]

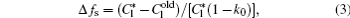
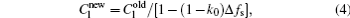
where 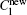
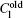
The alloys for the simulations of the CDT are succinonitrile– 0.1 mol% acetone (SCN– 0.1 mol% ace) and SCN– 0.2 wt% Salol, the thermal physical parameters are shown in Table 1.
| Table 1. Thermal physical parameters of succinonitrile (SCN), SCN-acetone, and SCN-Salol. |
The computational domain is 256 μ m× 2048 μ m for the 2D model, and the mesh size is 1.0 μ m. If the simulation needs more resolution, then the computational domain of 512 μ m× 4096 μ m can be used. At the beginning of the simulations, the bottom of the computational domain is a planar interface.
According to the KF criterion, Vcd = Vc/k0 = DlG/(Δ T0k0) = DlG/[mlC0(k0 − 1)], and Γ has no effects on the CDT.
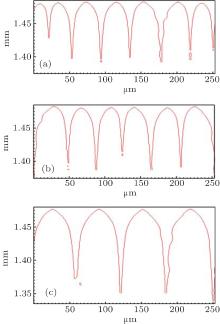
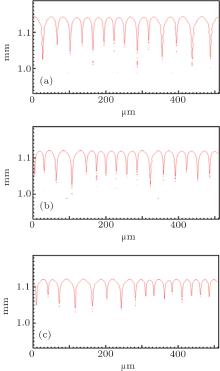
Figure 2 shows the simulation results with different Γ under unchanged conditions of V = 100 μ m/s, G = 15 K/mm, C0 = 0.1 mol% , ml = − 2.16 K/mol% , k0 = 0.103, and ɛ = 0.005. When Γ increases from 3.2× 10− 8 m· K to 9.6× 10− 8 m· K, both the cell and the dendrite spacings increase. However, it can be obviously seen that the changing of Γ has no effects on the CDT. The influence of Γ on the CDT agrees well with the KF criterion.
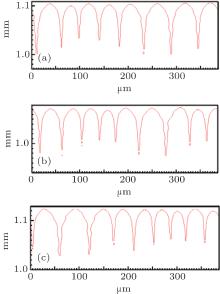
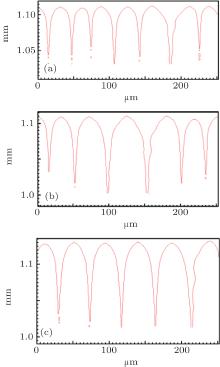
By using the same strategy, the solute diffusivity Dl, the initial composition C0, and the liquidus slope ml are also examined by the CA simulations, as shown in Figs. 3– 5. The corresponding changes in pulling velocities V or temperature gradient G are calculated according to the KF criterion. The simulation results show that the three physical parameters: ml, C0, and Dl also agree well with the prediction of the KF criterion.
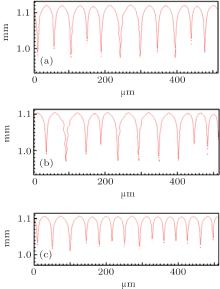
However, the solute partition coefficient k0 is very exceptional, which is the main finding of this paper. During the simulations, k0 was continually increased from 0.04 to 0.16 by an interval of 0.01. The pulling velocities were set close to the prediction of the KF criterion. Figures 6 (SCN-0.1 mol% ace) and 7 (SCN-0.2 wt% Salol) show the influence of k0 on the CDT, in which only k0 = 0.04, 0.10, and 0.16 are presented. The simulation results show that when k0 is small, the simulated morphologies are the CDT; and, when k0 is large, the morphologies are cellular. Figure 8 is the 3D simulation of the SCN-0.1 mol% ace with different k0. By comparing the 2D and 3D simulation results, it can be concluded that a similar influence pattern of k0 on the CDT is obtained. Overall, both the 2D and the 3D CA simulations show that the KF criterion is only validated when k0 is small.
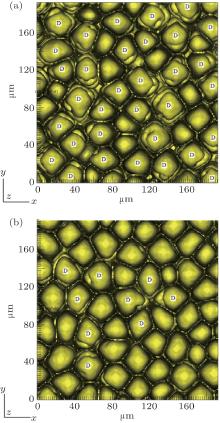 | Fig. 8. The 3D simulations of the CDT for SCN-ace alloy with solute partition coefficient conditions: (a) k0 = 0.10, G = 15 K/mm, V = 100 μ m/s, (b) k0 = 0.20, G = 15 K/mm, V = 112.5 μ m/s. |
To quantitatively understand the CDT, the relationship between λ c, max and λ cd should be analyzed. Teng et al.[10] have presented an expression of the λ cd by investigating through a thin film experiment
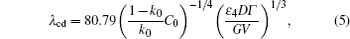
and Georgelin and Pocheau have presented a different expression of the λ cd

Hunt and Lu[27] presented a rough expression for the cell spacings. The phase field simulations[13, 23] evidenced that the relationship between the maximum finger spacing and the pulling velocity is 
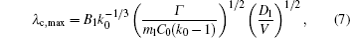
where B1 is constant.
Based on the investigations in present CA simulations and the KF criterion, the critical velocity Vcd of the CDT should follow the expression

where B2 is constant, f (ɛ ) and g (k0) are the unknown expressions of ɛ and k0.
By solving λ cd = λ c, max, one can obtain the expression of Vcd. Since equations (6) and (7) have the same V− 1/2, the Vcd cannot be obtained based on the two formulas. Equation (5) is selected to be a more appropriate formula to describe the λ cd. To get consistent results with Eq. (8), equations (5) and (7) are modified slightly as
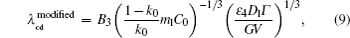
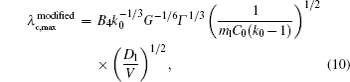
where B3 and B4 are constant.
The modifications are based on the following considerations. The 
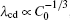
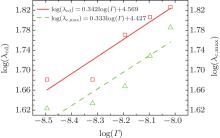 | Fig. 9. Plots of log(λ cd)– log(Γ ) and log(λ c, max)– log(Γ ) based on the data in the present CA simulations. |
Overall, based on Eqs. (8)– (10), one can get a self-consistent relationship among λ c, max, λ cd, and Vcd. By solving λ cd = λ c, max, we can obtain the exact expression of Vcd. However, the influence of the interface energy anisotropy ɛ on the λ c, max and λ cd are still unknown. Therefore, the influences of k0 and ɛ should be quantitatively investigated later.
In conclusion, the influences of the physical parameters (Γ , Dl, ml, C0) on the cell-to-dendrite transition in directional solidification are investigated by using CA simulations. It is evidenced that Gibbs– Thomson coefficient Γ has no effects on the CDT. It is also found that the influences of the physical parameters (Dl, ml, C0) exactly follow the Kurz and Fisher (KF) criterion. The most important finding in this paper is that when k0 is small, the influences of k0 on the CDT agree with the KF criterion; and, when k0 is larger than 0.16, the Vcd is higher than the prediction of the KF criterion. The special performance of k0 on the CDT could explain why SCN-ace and SCN-Salol have different behaviors on the CDT. Based on the simulation results, the expressions of the cell spacing λ c, max and the critical spacing λ cd are modified to give a consistent formula to predict the CDT.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|