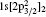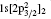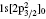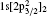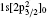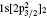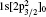Cite this Article
Ma Kun, Xie Lu-You, Zhang Deng-Hong, Dong Chen-Zhong†. Theoretical study on photorecombination of C V ion . Chinese Physics B, 24(7): 073402  
Permissions
Theoretical study on photorecombination of C V ion
Ma Kuna),b), Xie Lu-Youa), Zhang Deng-Honga), Dong Chen-Zhong†a)
Key Laboratory of Atomic and Molecular Physics & Functional Materials of Gansu Province, College of Physics and Electronic Engineering, Northwest Normal University, Lanzhou 730070, China
School of Information Engineering, Huangshan University, Huangshan 245041, China

†Corresponding author. E-mail: dongcz@nwnu.edu.cn

*Project supported by the National Natural Science Foundation of China (Grant Nos. 11274254, U1332206, and U1331122) and the International Scientific and Technological Cooperative Project of Gansu Province, China (Grant No. 1104WCGA186).

Abstract

The partial and total photorecombination cross sections of the ground-state C V ion in the KLL and KLM resonant energy regions were calculated in detail by using the Dirac atomic R-matrix code based on a fully relativistic R-matrix method. Meanwhile, the principal resonant lines in each photorecombination channel have been classified according to the calculated transition energies and probabilities from the KLL and KLM resonant states to the 1s2 nl ( n = 2, 3 and l = s,p,d) final states. The validity of these calculations is assessed by comparison with previously published experimental and theoretical data. The good agreement between the present calculated results and those obtained using different approaches confirms the accuracy of the present results. In addition, it is found that the damping effect can be neglected for the KLL resonant, but not for the KLM resonant.

PACS: 34.80.Lx; 34.10.+x
Keyword: photorecombination; R-matrix method; C V ion
1. Introduction

Photorecombination (PR) process is an important atomic process of interest in applied and fundamental physics.[1] This process may seriously affect the ionization balance and ionic excited-state distributions of laboratory and astronomical plasmas, as in fusion devices and in the solar corona, and it is also an important cooling mechanism of high-temperature plasmas.[2, 3] The PR process is generally treated as two independent processes. One process is a direct PR, i.e., the radiative recombination (RR) process, which is a direct transition from a free to a bound state with the emission of a photon. The other process is the well-known resonant PR, i.e., the dielectronic recombination (DR) process, which is the resonant capture of an electron by an ion followed by radiative stabilization through emission of one or more photons. However, from the point of view of quantum mechanics, all the PR processes, including RR and DR, can interfere near the resonance position if the initial and final atomic states are the same.

Theoretically, nonperturbative and perturbative approaches are used to investigate the PR process. The advantage of nonperturbative approach is that it automatically includes any quantum-mechanical interference between the resonant part (DR) and the nonresonant part (RR), the drawback is that it normally omits radiation damping. Although radiation damping is easily included by perturbative approach, [4– 6] it is impracticable to include all the perturbative orders in practical calculations. In view of the above, nonperturbative approaches, such as the close-coupling R-matrix theories of Burke, Hibbert, and Robb, [7, 8] are used in the present paper. Nahar and Pradhan[9– 11] pointed out that the photoionization (PI) cross sections calculated in the close-coupling approximation and by the R-matrix method may be employed to treat the PR process without the physically artificial distinction between the DR and RR processes. Then, a series works[6, 12– 19] have been reported on a PR process based on the method and good results have been obtained. In Zhao et al.’ s work, [6] they presented a numerical method to calculate the low-lying resonance PR by evaluating the Cauchy principal value of the integral in scattering matrices directly. This method was developed within the framework of the rigorous continuum-bound transition of Davies and Seaton, [20] and the radiation damping effect could be considered simply. In the experimental aspect, the DR and RR interferences in highly charged U (Z = 92) ions have been observed at the super-EBIT facility of the Lawrence Livermore National Laboratory, [21] and then the interference was also observed for Hg (Z = 80) ions with the Heidelberg EBIT[22] and for Bi (Z = 83) ions with the Tokyo EBIT.[23, 24]

In the present work, based on the work of Nahar and Pradhan, the PR process of C V ion in the low-lying resonant energy regions have been studied by using the Dirac atomic R-matrix code (DARC)[25] based on a fully relativistic R-matrix method. Firstly, the PI cross sections from C IV ground state and excited state to C V ground state are calculated by DARC. Then, the PR cross sections of C V ion in the ground state can be obtained based on the principle of detailed balance. The advantage of this method is that it can automatically include the interference of DR and RR processes, and a fully relativistic R-matrix method could include more detailed resonant structure. In addition, for identifying the principal resonant lines in each PR channel, the transition energies and probabilities from the KLL and KLM resonant states to 1s2nl (n = 2, 3 and l = s, p, d) states have been calculated by GRASP2K[26, 27] and RATIP[28] package based on the multiconfiguration Dirac– Fock (MCDF) method.

The remainder of this paper is organized as follows. In Section 2, the theoretical method is described briefly. In Section 3, the target energies, resonant energies, and the PR cross sections of C V ion in the KLL and KLM resonant energy regions are given. Finally in Section 4 conclusions are drawn.

2. Theoretical method

In this paper, the close-coupling approximation and the fully relativistic R-matrix method are employed to study the PR process. Here we present a brief description of the theory relevant to the calculations of PR cross sections.

2.1. R-matrix for photoionization

The PI process could be expressed as

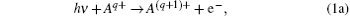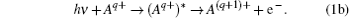Equation  (1a) denotes the direct PI and equation  (1b) denotes the resonant PI. The Dirac– Coulomb Hamiltonian for the (N + 1)-electron system of the initial PI process can be expressed in atomic units as

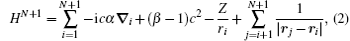
where i and j denote the individual electrons index, and α and β are the Dirac matrices. The first three one-electron terms on the right-hand side in the Hamiltonian are the momentum term, the mass term, and the electron– nucleus Coulomb attraction, respectively. The final two-electron term represents the Coulomb electron– electron repulsion.

The R-matrix theory divides configuration space into an inner and an outer region, separated by a spherical shell of radius ra centred at the nucleus. In the inner region, all N + 1 electrons are treated on an equal footing and all exchange effects are considered. The (N + 1)-electron wave function for the Jπ symmetry is given by

where are the target state wave functions coupled with the angular and spin parts of the incoming electron, A is the antisymmetry operator, uij is the continuum wave function of a free electron, and ϕ j is the (N + 1)-electron bound state wave function. The summation over i, j of the first term is over all open channels of and over all continuum electronic orbital uij to meet the Jπ symmetry. The summation over j of the second term is over all (N + 1)-electron bound states to ensure the completeness of the basis. 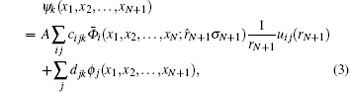In the outer region, the system is simplified as a two-body system where 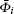the incoming electron is in a long-range multipole field. The wave functions in this region is given by

The parameters cijk and djk are calculated by diagonalizing the (N + 1)-electron Hamiltonian within the inner region of the R-matrix box. Then enforcing continuity at the boundary, we obtain the wavefunction in both regions with the R-matrix as a connection between the parts.

In Eqs.  (3) and (4), the relativistic electron wavefunction has the form of

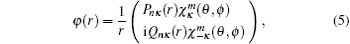
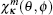
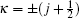
where Pnκ (r) and Qnκ (r) are the large and small component radial wave functions, respectively, the functions are the spin spherical harmonics, and κ is the relativistic angular quantum number of a continuum electron, for .

The PI cross-section can be expressed in dipole length form as

where g is the statistical weight of the initial state and SL is the generalized line strength, which include not only direct PI and resonant PI process, but also the interference of these two processes.[25]

In the present PI calculations, the continuum orbital with different angular momentum is expressed as a linear combination of 25 numerical basis functions. To resolve the fine resonant structure in the respective PR cross sections, a suitably chosen fine energy mesh of 10− 4  Ryd between the thresholds has been adopted.

2.2. R-matrix for photorecombination

Recombination of an incoming electron to the ground state of C V ion may occur through non-resonant background continuum, usually referred to as RR,

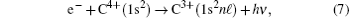
which is the inverse process of the direct PI, or through a two-step recombination process, i.e., dielectronic recombination (DR),

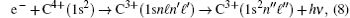
which is the inverse process of the resonant PI.

According to the principle of detailed balance (Milne relation), the relationship between the PR and PI cross-sections can be obtained as

where α is the fine structure constant, ε is the photoelectron energy, I is the ionization potential, and gi(gf) is the statistical weight of the recombined initial (final) state.

3. Calculation and discussion
3.1. Target state energies

The target state wavefunction of C V ions are described by 23 relativistic orbits: 1s1/2, 2s1/2, 2p1/2, 2p3/2, 3s1/2, 3p1/2, 3p3/2, 3d3/2, 3d5/2, 4s1/2, 4p1/2, 4p3/2, 4d3/2, 4d5/2, 4f7/2, 4f9/2, 5s1/2, 5p1/2, 5p3/2, 5d3/2, 5d5/2, 5f7/2, 5f9/2. All of these orbits are obtained by using the EOL scheme. In the RSCF of the GRASP2K[26, 27] and DSTG2 of the DARC[25] calculations, the target wavefunctions are generated by 1snl (n = 1, 2, 3, 4, 5, l = s, p, d, f), and their lowest 17 levels are included in the generation of channels.

Table  1 lists the target state energies of C V ion along with the data from the NIST database[29] for comparison. It can be seen that the energies calculated by MCDF agree well with DARC results for all of the above mentioned target states. However, there is about a 1  eV discrepancy between our results and NIST. This discrepancy is mainly caused by the remained electron correlation effects.

Table 1. The lowest seventeen energy levels in C V ion (in eV).
3.2. Transition energies and probabilities

Transition energies and transition probabilities of KLL and KLM resonant states to PR final state have been calculated by the component (REOS) of the RATIP package[28] and the results have been listed in Table  2, in which B and C denote the transition probabilities in Babushkin and Coulomb gauges, respectively. For the sake of simplicity, these resonant transition lines are ordered as a number, which are listed in the ‘ Label’ column of Table  2. It can be seen that the transition probabilities of the most lines listed in this table are in good agreement in the two different gauges, however, there is a relative lager divergence for some weaker transition lines, such as the transitions 53, 54, 65, 81, 87, 98, and 118. In fact, in these transition processes, the two electrons change and one photon emits simultaneously, which is the so-called TEOP transitions.[30– 33] For example, the transition 53 corresponds to the (1s2s)03p3/2J = 1/2 to the 1s23s J = 1/2 transition. The TEOP process was first theoretically predicted by Heisenberg[33] and it is mainly caused by strong configuration interactions. As can be seen from Table  2, the transition probabilities of these TEOP processes are relatively small in the present work.

Table 2. Transition energies and probabilities from the KLL and KLM resonant states to the PR final states.
3.3. The PR cross section

In this section, the PI cross sections of C IV ion from the 1s2nl (n = 2, 3, l = s, p, d) to the 1s2 have been calculated firstly by the DARC, and then the PR cross sections of C V ion from the 1s2 state to the 1s2nl (n = 2, 3, l = s, p, d) states will be obtained by the means of the principle of detailed balance. According to the Jπ symmetry, there are two PR channels for the recombined states 1s22s, 1s22p1/2, 1s23s, and 1s23p1/2, three PR channels for the recombined states 1s22p3/2, 1s23p3/2, 1s23d3/2, and 1s23d5/2. Partial PR cross sections for each channel of these PR processes have been shown in Figs.  1– 3. In these figures, the most of the distinguishable resonant lines have been labeled using the number in Table  2.

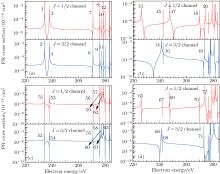Fig.  1. Partial PR cross sections of C V from 1s2 to recombined states (a) 1s22s, (b) 1s22p1/2, (c) 1s23s, and (d) 1s23p1/2.

Fig.  2. Partial PR cross sections of C V from 1s2 to recombined states (a) 1s22p3/2 and (b) 1s23p3/2.

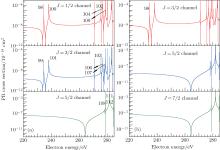Fig.  3. Partial PR cross sections of C V from 1s2 to recombined states (a) 1s23d3/2 and (b) 1s23d5/2.

The total PR cross sections of C V from the 1s2 to the recombined states 1s2nl (n = 2, 3, l = s, p, d) have been shown in Fig.  4. From this figure, we can see that there is a close relationship between the profile of the PR cross sections and the orbital angular quantum of recombined orbital. For example, the profile of 2s is similar to 3s, 2p1/2 and 2p3/2 are similar to 3p1/2 and 3p3/2, and so on.

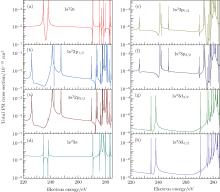Fig.  4. Total PR cross sections of C V from 1s2 to recombined states (a) 1s22s, (b) 1s22p1/2, (c) 1s22p3/2, (d) 1s23s, (e) 1s23p1/2, (f) 1s23p3/2, (g) 1s23d3/2, and (h) 1s23d5/2.

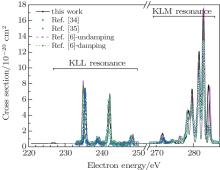
In order to test the validity of the above calculated results, we further obtain the composite PR cross sections of the C V ion in the ground state by summing over the total PR cross sections for each recombined final state, such as the ground state and 1s2nl (n = 2, 3, l = s, p, d) excited states. Then, we compare with the experimental results from Mannervik[34] and Mü ller, [35] and the perturbative theoretical results from Zhao.[6] The present calculated results are convolved with FWHM = 0.65  eV in the Gaussian distribution. To match the experimental results, the calculated resonant positions by us and Zhao have been shifted 0.8  eV and 0.4  eV, respectively, and the calculated cross sections have been shifted 0.4 × 10− 20  cm2. As shown in Fig.  5, there is a very good agreement for both the amplitude of the cross sections and the line shapes. However, there is a little discrepancy for the KLM resonant intensity. The present results are similar to Zhao’ s undamping results. However, Zhao’ s damping results reduce the KLM resonant intensity and better agree with the experimental results. Therefore, we can say that the damping effect is important for the KLM resonant, but not for the KLL resonant.

Fig.  5. The PR cross sections of C V ion in KLL and KLM resonant regions.

According to Pradhan et al., [36] the radiation damping contributions to the PR process depend on the ratio between the radiation width (Γ r) and the total width (Γ = Γ r + Γ a), where Γ a denotes the Auger width. In Table  3, the radiation and Auger widths of the KLL and KLM resonant states for C IV ion have been presented by the flexible atomic code (FAC).[37] As can be seen from this table, the radiation widths increase with the increase of energies of the resonant excited states. For example, for the resonant state 1s2s2, the ratio Γ r/Γ is 0.001%, but is 26.57% for the 1s2p3d state.

Table 3. Radiation and Auger widths of the KLL and KLM resonant states.
4. Conclusions

In summary, we employ a new version of R-matrix computer programs (DARC) to study the PR process, based on a fully relativistic R-matrix and the close-coupling method. The method not only includes non-resonant recombination and resonant recombination, but also the interference effects between the two, naturally.

On the basis of this scheme, the partial and total PR cross sections of C V ion for incident-electron energies in the vicinity of the KLL and KLM resonant regions, and transition energies and probabilities from the KLL and KLM resonant states to the 1s2nl (n = 2, 3, l = s, p, d) states have been given in detail. Meanwhile, the principal resonant lines in each PR channel have also been identified in the present work. In order to test the correctness of the present calculations, we compare our composite PR cross sections to the high-resolution experimental measurements and available theoretical calculations, and a good agreement demonstrates the reliability of the present calculations. However, in the KLM resonant region, the present PR cross sections are overestimated due to the neglect of the radiation damping effect.

Reference
1 Graham W G, Fritsch W, Hahn Y and Tanis J A 1992 Recombination of Atomic Ions, Vol.  269, in NATO Advanced Study Institute, Series B: Physics New York Plenum [Cited within:1]
2 Summers H P 1994 Adv. At. Mol. Opt. Phys. 33 275 DOI:10.1016/S1049-250X(08)60039-7 [Cited within:1]
3 Mason H E and Monsignori-Fossi B C 1994 Astron. Astrophys. Rev. 6 123 DOI:10.1007/BF01208253 [Cited within:1]
4 Wan J J and Dong C Z 2011 Phys. Scr. 84 045301 DOI:10.1088/0031-8949/84/04/045301 [Cited within:1]
5 Pindzola M S, Robicheaux F J, Badnell N R, Chen M H and Zimmermann M 1995 Phys. Rev. A 52 420 DOI:10.1103/PhysRevA.52.420 [Cited within:1]
6 Zhao L B, Ichihara A and Shirai T 2000 Phys. Rev. A 62 022706 DOI:10.1103/PhysRevA.62.022706 [Cited within:4]
7 Burke P G, Hibbert A and Robb W D 1971 J. Phys. B 4 153 DOI:10.1088/0022-3700/4/2/002 [Cited within:1]
8 Burke P G and Robb W D 1976 Adv. At. Mol. Phys. 11 143 DOI:10.1016/S0065-2199(08)60030-5 [Cited within:1]
9 Nahar S N and Pradhan A K 1991 Phys. Rev. A 44 2935 DOI:10.1103/PhysRevA.44.2935 [Cited within:1]
10 Nahar S N and Pradhan A K 1992 Phys. Rev. Lett. 68 1488 DOI:10.1103/PhysRevLett.68.1488 [Cited within:1]
11 Nahar S N and Pradhan A K 1994 Phys. Rev. A 49 1816 DOI:10.1103/PhysRevA.49.1816 [Cited within:1]
12 Gorczyca T W, Robicheaux F, Pindzola M S and Badnell N R 1996 Phys. Rev. A 54 2107 DOI:10.1103/PhysRevA.54.2107 [Cited within:1]
13 Mitnik D M, Pindzola M S and Badnell N R 1999 Phys. Rev. A 59 3592 DOI:10.1103/PhysRevA.59.3592 [Cited within:1]
14 Zhang H L, Nahar S N and Pradhan A K 1999 J. Phys. B 32 1459 DOI:10.1088/0953-4075/32/6/010 [Cited within:1]
15 Pradhan A K, Chen G X, Nahar S N and Zhang H L 2001 Phys. Rev. Lett. 87 183201 DOI:10.1103/PhysRevLett.87.183201 [Cited within:1]
16 Pradhan A K, Nahar S N and Zhang H L 2001 Astrophys. J. 549 L265 DOI:10.1086/319174 [Cited within:1]
17 Zhang H L, Nahar S N and Pradhan A K 2001 Phys. Rev. A 64 032719 DOI:10.1103/PhysRevA.64.032719 [Cited within:1]
18 Nahar S N and Pradhan A K 2004 Radiat. Phys. Chem. 70 323 DOI:10.1016/j.radphyschem.2003.12.019 [Cited within:1]
19 Stancalie V 2013 Eur. Phys. J. D 67 223 DOI:10.1140/epjd/e2013-40326-8 [Cited within:1]
20 Davies P C W and Seaton M J 1969 J. Phys. B 2 757 DOI:10.1088/0022-3700/2/7/304 [Cited within:1]
21 Knapp D A, Beiersdorfer P, Chen M H, Scofield J H and Schneider D 1995 Phys. Rev. Lett. 74 54 DOI:10.1103/PhysRevLett.74.54 [Cited within:1]
22 González Martínez A J, Crespo López-Urrutia J R, Braun J, Brenner G, Bruhns H, Lapierre A, Mironov V, Soria Orts R, Tawara H, Trinczek M, Ullrich J and Scofield J H 2005 Phys. Rev. Lett. 94 203201 DOI:10.1103/PhysRevLett.94.203201 [Cited within:1]
23 Tobiyama H, Nohara H, Kavanagh A P, Nakamura N, Watanabe H, Sakaue H A, Li Y, Kato D, Currell F J, Yamada C and Ohtani S 2007 J. Phys. : Conf. Ser. 58 239 DOI:10.1088/1742-6596/58/1/051 [Cited within:1]
24 Nakamura N, Kavanagh A P, Watanabe H, Sakaue H A, Li Y, Kato D, Currell F J, Tong X M, Watanabe T and Ohtani S 2009 Phys. Rev. A 80 014503 DOI:10.1103/PhysRevA.80.014503 [Cited within:1]
25 Norrington P H 2004www.am.qub.ac.uk/DARC [Cited within:3]
26 Jönsson P, He X, Fischer F C and Grant I P 2007 Comput. Phys. Commun. 177 597 DOI:10.1016/j.cpc.2007.06.002 [Cited within:2]
27 Grant I P 2007 Relativistic Quantum Theory of Atoms and Molecules Berlin Springer [Cited within:2]
28 Fritzsche S 2012 Comput. Phys. Commun. 183 1525 DOI:10.1016/j.cpc.2012.02.016 [Cited within:2]
29 Kramida A, Ralchenko Y and Reader JNIST ASD Team 2013 NIST Atomic Spectra DatabaseVer. 5. 1 [Cited within:1]
30 Heisenberg W 1925 Z. Phys. 32 841 DOI:10.1007/BF01331720 [Cited within:1]
31 Goudsmit S and Gropper L 1931 Phys. Rev. 38 225 DOI:10.1103/PhysRev.38.225 [Cited within:1]
32 Wölfli W, Stoller C, Bonani G, Suter M and Stöckli M 1975 Phys. Rev. Lett. 35 656 DOI:10.1103/PhysRevLett.35.656 [Cited within:1]
33 Salem S I, Kumar A, Soctt B L and Ayers R D 1982 Phys. Rev. Lett. 49 1240 DOI:10.1103/PhysRevLett.49.1240 [Cited within:2]
34 Mannervik S, Asp S, Broström L, DeWitt D R, Lidberg J, Schuch R and Chung K T 1997 Phys. Rev. A 55 1810 DOI:10.1103/PhysRevA.55.1810 [Cited within:1]
35 Mul̈ler A, Schippers S, Phaneuf R A, Scully S W J, Aguilar A, Covington A M, Aĺvarez I, Cisneros C, Emmons E D, Gharaibeh M F, Hinojosa G, Schlachter A S and McLaughlin B M 2009 J. Phys. B 42 235602 DOI:10.1088/0953-4075/42/23/235602 [Cited within:1]
36 Pradhan A K and Zhang H L 1997 J. Phys. B 30 L571 DOI:10.1088/0953-4075/30/17/004 [Cited within:1]
37 Gu M F 2008 Can. J. Phys. 86 675 DOI:10.1139/P07-197 [Cited within:1]