†Corresponding author. E-mail: fhym@ustc.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 11175113).
Based on the operator Hermite polynomials method (OHPM), we study Stirling numbers in the context of quantum mechanics, i.e., we present operator realization of generating function formulas of Stirling numbers with some applications. As a by-product, we derive a summation formula involving both Stirling number and Hermite polynomials.
In mathematical physics and quantum statistics, the Stirling numbers are frequently used.[1] The Stirling numbers of the first kind, which count the number of permutations of m elements with k disjoint cycles, are the coefficients in the expansion
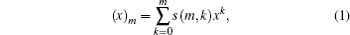
where (x)m (a Pochhammer symbol) denotes the falling factorial,
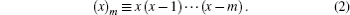
The Stirling numbers of the second kind[2, 3] count the number of ways to partition a set of m elements into k nonempty subsets, defined by
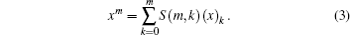
The purpose of this paper is to study the Stirling numbers in the context of quantum mechanics, i.e., we shall present the operator realization of generating functions of Stirling numbers by virtue of the operator Hermite polynomials method (OHPM).[4– 6] In other words, we search for operator realization for deriving generating functions S(m, k) and s(m, k), which bear some physical meaning in the realization itself. We also study some combination of Stirling numbers with Hermite polynomials.
Hermite polynomials Hn (x), as a special function, is very useful in quantum mechanics and mathematical physics. Physically, Hn (x) is the eigenfunction of harmonic oscillator.[7] The essence of OHPM is to replace the usual Hermite polynomials Hn (x) by Hn (X), where 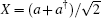

and
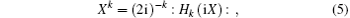
where : : denotes normal ordering. In some preceding papers, [10, 11] we have employed them to derive the binomial theorem involving Hermite polynomials

As its application, we can deduce the following new formula:
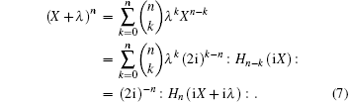
Furthermore, performing derivative for the right-hand side of Eq. (6)

On the other hand, performing derivative for the left-hand side of Eq. (6)
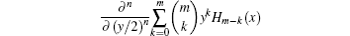
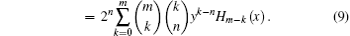
By comparing Eq. (9) with Eq. (8), we obtain another generalized binomial theorem involving Hermite polynomials
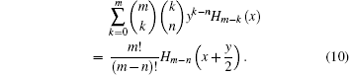
In Sections 3 and 4 we shall respectively employ the OHPM to examine generating functions of Stirling numbers with some applications.
Lemma 1 Let the power series expansion (in terms of x) of 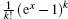

then A(n, k) is equal to
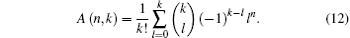
Proof We use OHPM. Instead of directly considering 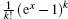
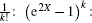
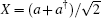
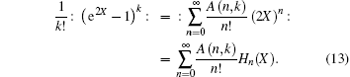
On the other hand
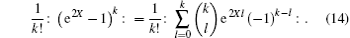
Using the Baker– Hausdorff formula we have

Substituting Eq. (15) into Eq. (14) yields

By comparing Eq. (16) with Eq. (13), we can identify

which determines
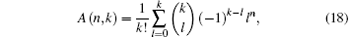
and converts
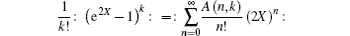
back to
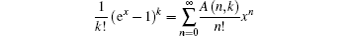
has no obstacles, thus the Lemma is proved.
Next we should examine if A(n, k) in Eq. (12) is just equal to the Stirling number of the second kind S(n, k). This constitutes Theorem 1.
We still adopt quantum mechanical operator approach. By considering operator 
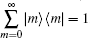

then

Substituting

and Eq. (19) into Eq. (20) yields

which leads to

This is in the same form as the definition of the Stirling number of the second kind in Eq. (3). Hence,
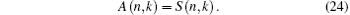
The proof is completed. Thus, equation (23) reveals the meaning of Stirling numbers in the Fock space.
As a by-product, now we know from Eqs. (13) and (4) that


Replacing X → x, we have a new summation formula involving both Stirling number and Hermite polynomials

This new formula is useful, because it provides opportunity of employing Hermite polynomials’ property to deduce characters of the Stirling numbers, for example,
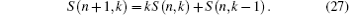
We also know

Letting N → x, we have
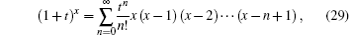
which is another kind of Newton binomial theorem.
Theorem 1 Let the power series expansion (in terms of t) of 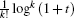

then s(n, k) is the Stirling number of the first kind.
Proof Instead of directly considering 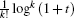
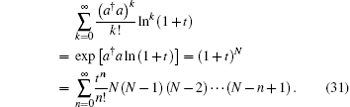
On the other hand, according to Eq. (30)

Comparing Eq. (30) with Eq. (31) leads to
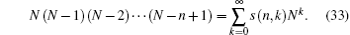
This is just the definition of Stirling number of the first kind in Eq. (1), so equation (28) reflects the generating function of s(n, k).
Using Eqs. (24) and (4), we consider

On the other hand,
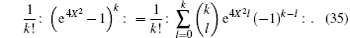
Using the technique of integration within ordered product (IWOP) of operators[11, 12] we can obtain

By substituting Eq. (36) into Eq. (35) and comparing with Eq. (34), we have
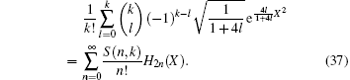
Comparing Eq. (37) with Eq. (12) we obtain the generating function formula of even-order Hermite polynomials
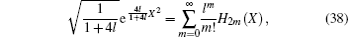
we can identify 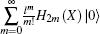

so

is really a squeezed state.
In summary, for the first time we use OHPM to study the Stirling numbers theory, we have found quantum mechanical operator realization for generating functions S(m, k) and s(m, k), which bear some physical meaning in the realization itself. As a by-product, we derived a summation formula involving both Stirling number and Hermite polynomials.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|


