†Corresponding author. E-mail: jswang@mail.qfnu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11347026, 11147009, and 11244005), the Natural Science Foundation of Shandong Province, China (Grant Nos. ZR2013AM012 and ZR2012AM004), and the Scientific Research Project of Liaocheng, China.
Using the well-behaved features of the thermal entangled state representation, we solve the diffusion master equation under the action of a linear resonance force, and then obtain the infinitive operator-sum representation of the density operator. This approach may also be effective for treating other master equations. Moreover, we find that the initial pure coherent state evolves into a mixed thermal state after passing through the diffusion process under the action of the linear resonance force.
In quantum optics, solving master equations describing interactions between fields and external environments is gradually becoming a hot topic, since quantum dissipation is unavoidable in the transmission of optical fields through media and this process can destroy nonclassicality of the fields. As shown in the literature, [1– 3] solving the master equations usually employs either the Fokker– Planck equation or the Langevin equation through inserting the density operators into the P-representation or the Wigner representation.[4, 5] Later, it was pointed out in Refs. [6]– [9] that the thermal entangled state representation can help one tackle these master equations conveniently because of some well-behaved properties of the entangled states. In this paper, we adopt the entangled state approach to treat the diffusion master equation under the action of a linear resonance force. Thus we establish a fresh picture of the time evolution of density operators by virtue of the thermal entangled state representation instead of the P-representation or the Wigner function.
The paper is arranged as follows. In Section 2, based on the well-behaved properties of the entangled state representation, we concentrate on solving the diffusion master equation under the action of a linear resonance force and give the infinitive operator-sum representation of the density operators. In Section 3, we prove the normalization of the infinitive operator-sum representation. In Section 4, we investigate the time-evolution rule of coherent states in a diffusion process acted upon by a linear resonance force.
A diffusion process under the action of a linear resonance force can be described by the master equation
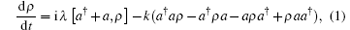
where parameters λ and k denote the resonance force strength and the decay rate, respectively. Usually, the master equation (1) is used to describe decoherence. In particular, the system is only acted upon by the linear resonance force when k = 0. Also, for λ = 0, equation (1) describes the pure diffusion process of a light field. To solve the master equation (1), we introduce the thermal entangled state representation, [10] which is defined in the enlarged Fock space
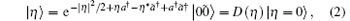
where
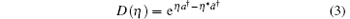
is the displacement operator, and
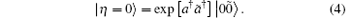
Here we need to point out that ã † is the operator of a fictitious mode corresponding to the real photon creation operator a† , ã can annihilate | 0̃ 〉 and has the relations [ã , ã † ] = 1 and [a, ã † ] = 0. Moreover, the state | η 〉 is the common eigenvector of (a − ã † ) and (a† − ã ), i.e.,
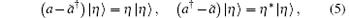
and the set of | η 〉 forms a complete entangled state representation
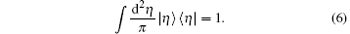
On the other hand, one can easily find that | η = 0〉 possesses the following properties:
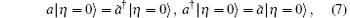
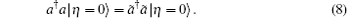
Using the above well-behaved properties of | η = 0〉 , master equations for the diffusion process under the action of the linear resonance force can be concisely solved. In the following, we will provide a detailed derivation. Denoting | ρ 〉 = ρ | η = 0〉 = ρ | I〉 and with both sides of Eq. (1) acting on state | η = 0〉 , we have
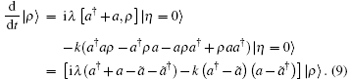
Thus, its formal solution is
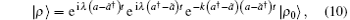
where ρ 0 is the initial density operator, | ρ 0〉 = ρ 0| I〉 . Now inserting the completeness relation of | η 〉 into the right side of Eq. (10) and employing the eigen-vector equation (5), we obtain ruleup
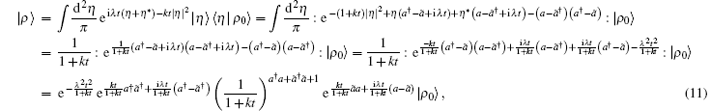
where we have used the normally ordered form of the vacuum projector[11] (the mark : : denotes normal ordering)
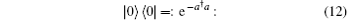
and the operator identity[11]
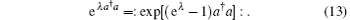
Further, using the relations (7) and (8), we can rewrite Eq. (11) as
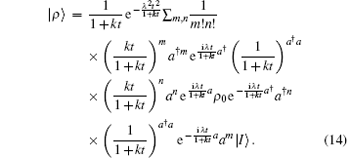
Then we obtain the solution to Eq. (1)

which is just an infinitive operator-sum form of the density operator ρ (t). From Eq. (15), we can clearly see that the infinitive operator-sum form is very useful, since for any given initial state ρ 0, the evolution density operator ρ (t) can be directly calculated. By defining the Kraus operator Mm, n corresponding to ρ (t)

we can further rewrite Eq. (15) as
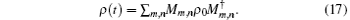
To show that equation (15) is qualified to be an infinitive operator-sum representation, we must check the normalization condition
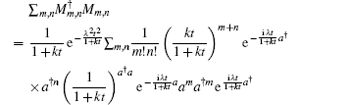
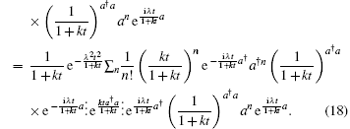
By using the operator identity[11]
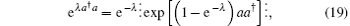
where the symbol ⋮ ⋮ represents the anti-normal ordering, equation (18) becomes
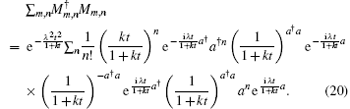
Noticing the operator formula
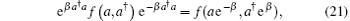
we have

Using the relation eAeB = eBeAe[A, B] yields the condition [A, B] ≠ 0, therefore
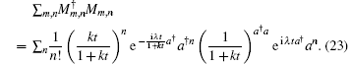
At last, using Eqs. (12) and (20), we obtain

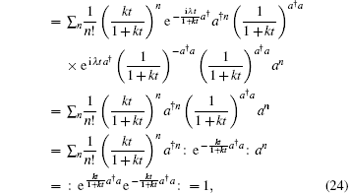
so the normalization of Mm, n holds, and thus
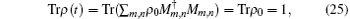
which exhibits that Mm, n is a trace-preserving quantum operation and the density operator ρ (t) is qualified to be an infinitive operator-sum representation.
Now we want to investigate how the coherent state ρ 0 = | α 〉 〈 α | [12] as an initial state evolves in the diffusion process acted upon by a linear resonance force. From Eq. (15), we obtain
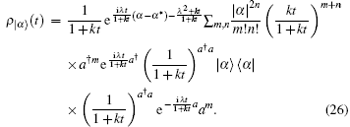
Inserting the operator identity
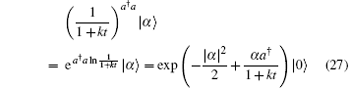
and the vacuum state projector (12) into Eq. (26) leads to the normal ordering form of ρ | α 〉 (t)

Using Eq. (13), we obtain
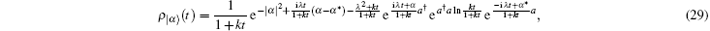
which is just a superposition of the photon-added mixed state. Therefore, after undergoing the diffusion process under the action of the linear resonance force, the pure coherent state evolves into a mixed state owing to the existence of quantum noise.
we have obtained the explicit solution of the diffusion master equation under the action of a linear resonance force and found the infinite-sum representations for the density operators of this process. For some other master equations of density operators, we also employ this method and obtain the explicit infinite-sum representations for the density operators. Finally, we find that the initial pure coherent state evolves into a mixed thermal state as a result of diffusion and linear resonance force.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|


