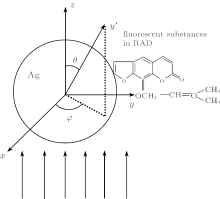
As shown in Fig.  1, we consider a system of a silver sphere with a RAD attached to it. The silver sphere has a radius r and is placed at the origin of a coordinate system. The incident plane wave polarizes in the x direction and propagates along the z direction. We assume that only the dipole oriented along the x axis is excited.^[16]

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Sketch of the system.

Firstly, we use a sphere with a radius of 21  nm, whose LSPR band peak is close to the excitation wavelength 315  nm of RAD. For a weak excitation, such as RAD, the excited rate for a two-level system is proportional to the absolute square of the exciting electric field E.^[17] The electric field of the incident wave can be expressed as

where k = 2π /λ . The interaction between the incident field and the silver sphere creates a scattered field E_s, which can be calculated by the Mie theory.^{[18, 19]} The local field can be expressed as

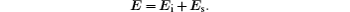
The RAD is excited by the local field. The excitation enhancement factor can then be defined as

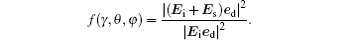
The averaged enhancement factor can be written down as^{[20– 22]}

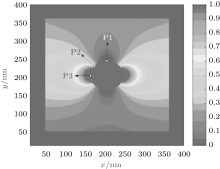
Based on the above theory, we calculate the enhancement factor of the local field around the silver sphere in different orientations by the FDTD method. The field distribution is shown in Fig.  2. The field enhancement regions are concentrated in close vicinity to the surface of the metal sphere, and they can be up to several tens of nanometers.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. The local field calculated for the silver sphere (r = 21  nm) via FDTD method.

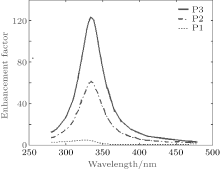
The maximal enhancement factor of the local field can reach up to three orders of magnitude. We exploit the enhancement factors at θ = π /2 and φ = 0, π , which are shown as points P1, P2, and P3 in Fig.  2. Point P1 is placed perpendicularly to the polarization direction, which is the orientation that has the maximum enhancement factor, Point P2 is placed at an angle of 45° relative to the polarization direction, and point P3 is along the polarization direction. All of these three points are in the xy plane. Figure  3 shows the field enhancement factors of points P1, P2, and P3. The enhancement factor is maximum at point P3, which can be up to nearly 120. The enhancement factor is nearly 60 at point P2 and is less than 10 at point P1. The plasmonic near field is distributed with a maximum along the illumination light polarization, which results in the different enhancement of the local field at the three different points.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. The enhancement factors at the three points P1, P2, and P3.

Figure  4 shows the distance-dependent electric field enhancement factor calculated by the Mie theory, and the data are taken along the polarization axis. As shown in Fig.  4, the average electric field enhancement around the Ag nanoparticle decreases quickly as the distance increases. When the distance between the RAD and the sphere is about 20  nm, the field enhancement factor can reach to 125, and it then decreases as the distance increases. The enhancement factor is only several when the distance is larger than 50  nm. This trend of the local field enhancement means that the plasmon resonance decays exponentially. We believe that the plasmonic effect on the luminous enhancement in the near-field region is more pronounced than that in the far-field region.^[23]

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. The excitation enhancement factor versus the distance away from the center of a 21  nm silver sphere.

We then consider the situation that the LSPR band of the sphere coincides with RAD’ s radiation wavelength. We use a sphere with a radius of 38  nm, whose LSPR band centers at the emission wavelength of 400  nm of RAD. The LSPR introduces an inhomogeneous environment for the oscillating dipole. Figure  5 shows the extinction spectrum of the silver sphere. For the silver sphere, the quadrupole resonance occurs near 310  nm. The dipole plasmon resonance peaks shifts to near 400  nm, which coincides with RAD’ s emission wavelength. In the vicinity of the silver sphere, the RAD at the excited state can undergo nonradiative decay, emit a photon directly to the far field, or relax rapidly by exciting the LSPR of the sphere via energy transfer. The LSPR can alter both the radiative and the nonradiative decay rates owing to the localized photonic states introduced by the plasmon resonance. Once the LSPR is excited, it can either decay nonradiatively due to internal damping or reradiate into the far field at the emission wavelength.^{[9, 22]}

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. The extinction spectrum of the silver sphere (r = 38  nm) obtained with the Mie theory.

As reported in Refs.  [15] and [18], the enhancement factor of the radiative rate is

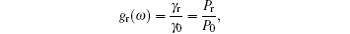
and the energy transfer factor is

where γ ₀ is the free emission decay, P₀ is the radiation power of the isolated dipole, the total decay rate γ can be divided into a radiative part and a non-radiative part, γ = γ _r + γ _nr, P_r is the radiation power to the far-field, P_abs is the radiation power absorbed by the environment, and g_r(ω ) and g_ET(ω ) are related to the corresponding cross sections. The emission enhancement factor g_em(ω ) can be given as^{[18, 21]}

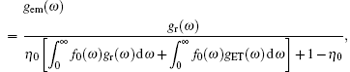
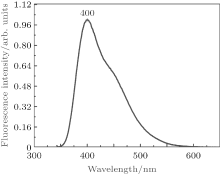
where f₀(ω ) is the integral-normalized emission spectrum of RAD in aqueous solution, and the measured emission spectrum is shown in Fig.  6, the emission peak of RAD is at 400  nm. The η ₀ is the quantum efficiency of the isolated molecule, which is η ₀ ≈ 0.15 for RAD. The fluorescence emission spectrum of RAD is obtained as

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. The amplitude-normalized emission spectrum of RAD in aqueous solution.

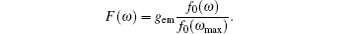
Figure  7 shows the emission enhancement factor calculated for RAD in the vicinity of the single silver sphere (r = 38  nm). As shown in Fig.  7, the enhancement at 400  nm is maximum due to the spectrum overlap between the LSPR band and the emission band of RAD, the largest emission enhancement can reach up to 9 times. The single silver sphere whose resonance wavelength coincides with the emission wavelength enhances the fluorescence emission, however, the enhancement is limited. If the quantum efficiency is too high, then the fluorescence emission would even be quenched.^{[17, 24]}

Fig.  7.

	Figure Option ViewDownloadNew Window
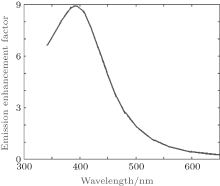	Fig.  7. The emission enhancement factor for RAD in the vicinity of the single silver sphere (r = 38  nm).

For the excitation process, the incident plane wave interacts with the silver sphere, and the plane wave does not change with the distance. For the emission process, the interaction is between the near field of the dipole and the silver sphere. Unlike the plane wave, the dipole field decreases quickly as the distance becomes longer, this is why the excitation enhancement is greater than the emission enhancement.