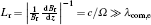In a vacuum, a photon can always metamorphose into an electron and a positron and then annihilate each other becoming a photon again within a short time mandated by the uncertainty principle. The process keeps on repeating itself. The electron and positron can also interact by exchanging a photon or more photons. Therefore, the vacuum is polarized and magnetized by strong fields and exhibits nonlinear optical characteristics.^{[1– 13]} In a static or rotational magnetic field, the vacuum leads to birefringence^{[4, 5, 7, 8, 14]} for the probe waves. Until now, the experimental results^{[5, 6]} are so close to the birefringence predicted by the existing theories.^{[4, 7, 8]} Heyl and Shaviv^[5] calculated the direction dependence of the refractive index and the polarization evolution of a probe wave in a strong rotational magnetic field. Based on the Maxwell equations, accompanied with the rotational magnetic field B_r, a strong rotational electric field E_r exists. Due to the electric field E_r, the phase velocity, the group velocity, and the refractive index of the probe wave depend on the angle between the wave vector and E_r × B_r and the phase of the strong electromagnetic field B_r. To check the light– light diffraction experimentally, King, Piazza, and Keitel^{[16, 17]} proposed a matterless double-slit scenario by using head-on collisions of a probe laser field with two ultra-intense laser beams. Kryuchkyan and Hatsagortsyan^[9] predicted the “ brag scattering” rate of a probe wave by spatially modulated strong electromagnetic fields. The phase and direction dependence of the refractive index, the relative permittivity, and the relative permeability of a probe wave in a strong rotation electromagnetic field have not been discussed in detail, but they are significant for the calculation of the polarization evolution, which maybe helpful for observations to distinguish emissions from a pulsar and to deduce the structure of the magnetosphere.^{[15, 18– 20]}

The photon polarization tensor is a powerful tool for describing the vacuum polarization in a homogeneity magnetic field, ^{[21, 22]} an electric field, ^[22] or an electromagnetic field.^{[23, 24]} With the photon polarization tensor, researchers investigated the angle dependence of vacuum birefringence^[25] in a homogeneous magnetic field, the amplitude for the scattering of a photon^{[26, 27]} by an intense laser field, and the light diffraction.^[28] However, the phase and direction dependence of photorefraction in a circular-polarized plane wave has not been discussed in detail.

Without using the photon polarization tensor, there is another simple and effective method to obtain the refractive index from the dispersion relationship by solving the Maxwell equations corrected by the effective Lagrangian 𝔏 _eff^[29] in a homogeneous^{[4, 7, 8]} or slowly-varying field. By using this method, in this paper, the refractive index of a probe wave with an arbitrary incident angle in the presence of a rotational strong electric and a rotational strong magnetic field is studied. With the obtained dispersion relationship of the probe wave, the phase and direction dependence of the refractive index, the permittivity, and the permeability are calculated in detail. It may provide a valuable theoretical basis to calculate the polarization evolution of waves in the strong electromagnetic circumstances of pulsar^[30] or neutron stars^{[19, 20, 31, 32]} and to understand the atmospheric emission of neutron stars.^{[32– 37]}

The external field is assumed to be a low-frequency strong circular-polarized electromagnetic wave,

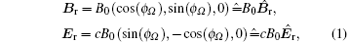
where ϕ _Ω = Ω t – k_rz, k_r = Ω /c, the vacuum light velocity is c = 3.0 × 10⁸ m/s, and cB₀ ≲ 10¹⁸ V/m, which is the critical Schwinger field of electron– positron pair production in the vacuum.

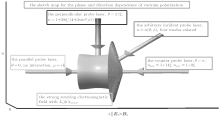
Now assume that the wave vector of the probe wave is k_p = (k sin(θ )cos(ϕ ), k sin(θ )sin(ϕ ), k cos(θ )) in the rotation coordinate system (Ê _r, B̂ _r, ẑ ), where θ and ϕ are the angle between k_p and ẑ and the angle between the projection of k_p on the Ê _r– B̂ _r plane and Ê _r, respectively.

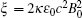
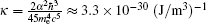
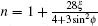
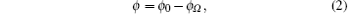
Figure 1 shows four cases as follows. (i) There is no interaction between the parallel incident probe wave and the rotational magnetic and electric field. (ii) The refractive indices of the parallel polarized probe wave and the perpendicular polarized probe wave are 1+ 14ξ and 1 + 8ξ , respectively, with , where ε ₀ is the permittivity of the vacuum, , m_e is the electron static mass, and α is the fine-structure constant. (iii) There is only one-permissible mode with the refractive index, in the perpendicular direction, which depends on the phase of the rotation field, ϕ . (iv) There are four possible modes for other cases, in which the incident angle of the probe wave is arbitrary. The details are given next by solving the Maxwell equations corrected by the effective Lagrangian 𝔏 _eff.^[29] Therefore, the scaling length of the rotational field must be much longer than the Compton wavelength of an electron, i.e., the frequency of the rotational field satisfies Ω ≪ c/λ _{com, e} ≈ 10²⁰ rad/s. Since k_p does not depend on Ω in the laboratory coordinate system, we have

where ϕ ₀ − π /2 is the angle between the projection of k_p on the x̂ – ŷ plane and the x axis. Set

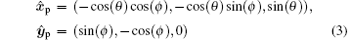
in the rotational coordinate system. Therefore, (x̂ _p, ŷ _p, k̂ _p = k_p/k_p) is a new unit orthogonal basis. After some algebra, we obtain

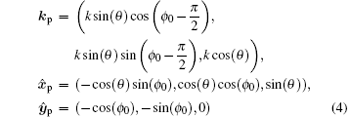
in the laboratory system (x̂ , ŷ , ẑ ). Therefore, the electromagnetic field of the probe wave satisfies

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The sketch map for the phase and direction dependence of vacuum polarization of a probe wave in a strong rotating electromagnetic field with the scaling length , where λ com, e ≈ 2.4263 × 10− 12 m is the Compton wavelength of an electron.

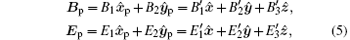
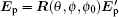
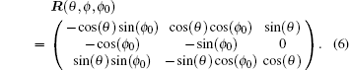
where the components in the rotational system (x̂ _p, ŷ _p, k̂ _p) and the components in the laboratory system (x̂ , ŷ , ẑ ) satisfy the rotational transformation, , with

With E₃ = 0, we obtain

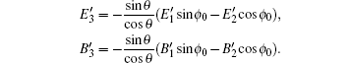
With the effective Lagrangian 𝔏 _eff, ^[29] the nonclassical electric displacement field D_p = D − ε ₀E_r and magnetic field strength 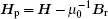are given by

where the tensors ϵ ^r, μ ^{– 1, r} in the rotational system and those in the laboratory system satisfy ϵ ^r = ϵ ^LR and μ ^{– 1, r} = μ ^{– 1, L}R. The ϵ ^r and μ ^{– 1, r} are expressed as

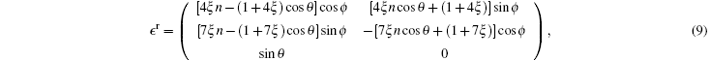
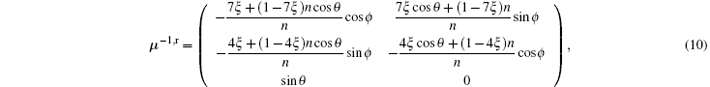
where n = ck/ω is the refractive index.

With the wave assumption and the linearization of the Maxwell equations corrected by the effective Lagrangian 𝔏 _eff, the dispersion relationship is obtained after some straightforward algebra

It contains three special cases for θ = 0, θ = π , and θ = π /2.

If θ = 0, the dispersion relationship becomes two second-order equations with roots of 1, − 1− 14ξ for the parallel polarization and roots of 1, − 1− 8ξ for the perpendicular polarization. The − 1− 14ξ and − 1− 8ξ correspond to the back-propagation waves. Therefore, there is no interaction between the forward-propagating wave and the rotational field.

If θ = π , the dispersion relationship has roots of – 1, 1 + 14ξ for the parallel polarization and roots of – 1, 1 + 8ξ for the perpendicular polarization. The refractive indices are the same as those in the static strong magnetic field.^{[4, 7]}

If θ = π /2, the dispersion relationship becomes

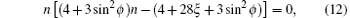
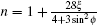
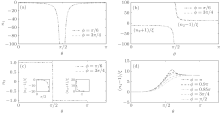
therefore, the refractive index is . There is only one-permissible mode in the perpendicular direction, i.e., k_p ⊥ ẑ . For ϕ = 0, i.e., k_p ∥ Ê _r, the refractive index of the probe wave propagating along the direction of E_r reaches the maximum value, n = 1 + 7ξ . For ϕ = π /2, i.e., k_p ∥ B̂ _r, the refractive index of the probe wave propagating along the direction of B_r reaches the minimum value, n = 1 + 4ξ . For different times or positions, the phases are different, and then the refractive indices are different. Therefore, the polarization of the mode in the perpendicular direction changes with the propagating path in the rotational electromagnetic field.

Figure 2 shows the direction dependence of the refractive indices. There are four modes for an arbitrary incident angle. The n₁ satisfies n₁ ≤ − 1 and decreases with increasing θ for θ ∈ [0, π /2) and increases for θ ∈ (π /2, π ]. The n₂ satisfies n₂ < − 1 for θ ∈ [0, π /2) and n₂ > 1 for θ ∈ (π /2, π ]. The n₁ and n₂ cannot reach a finite value at θ = π /2. The n₃ satisfies n₃ ≤ 1 for θ ∈ [0, π /2) and n₃ > − 1 for θ ∈ (π /2, π ], and becomes zero at θ = π /2. The n₄ increases with increasing θ for ϕ ≤ 3π /4 and reaches the maximum value at θ ≈ 3π /5 for ϕ > 3π /4. For θ = π /2, .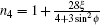

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The direction dependence of the refractive indices of a probe wave in a strong circular-polarized electromagnetic field. There are four modes for θ ≠ π /2. (a) Negative n1; (b) (n2 + 1)/ξ for θ ∈ [0, π /2) and (n2 − 1)/ξ for θ ∈ (π /2, π ]; (c) n3; (d) (n4 − 1)/ξ .

Figures 3 and 4 show the phase dependence of the refractive indices. The n₁ satisfies n₁ ≤ − 1 and reaches the maximum value at the axis of symmetry, ϕ = π /2. The n₂ reaches the minimum (maximum) value at the symmetry axis for θ < π /2 (θ > π /2). The n₃ satisfies n₃ ≤ 1 and reaches the minimum value at the axis of symmetry for θ < π /2. For θ > π /2, n₃ ≥ − 1 and reaches the maximum value at the axis of symmetry for θ < π /2. The n₄ reaches the minimum value at the symmetry axis.

Fig. 3.

	Figure Option ViewDownloadNew Window
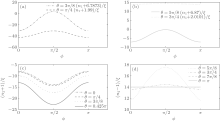	Fig. 3. The phase dependence of the refractive indices of a probe wave in a strong circular-polarized electromagnetic field: (a), (b) n1; (c), (d) n2.

Fig. 4.

	Figure Option ViewDownloadNew Window
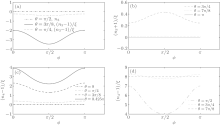	Fig. 4. The phase dependence of the refractive indices of a probe wave in a strong circular-polarized electromagnetic field: (a), (b) n3; (c), (d) n4.

With the refractive indices and Eqs. (9) and (10), the phase dependence of the permittivity ε ^L and the permeability μ ^L corresponding to the four refractive indices can be obtained. Since the four components, , , , and , , , , are the most important, they are prominently discussed as follows. (i) and are approximate units. (ii) and are of the same order as ξ . (iii) and . They all depend on the quantum parameter ξ and the phase angle ϕ . Specially ε ₂₁ ≈ 1 and ε ₂₂ ≈ 0 for ϕ ≈ π /2. For ϕ ⪆ 0, ε ₂₁ ⪅ 0.

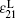
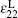
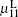
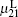
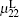
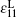
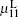
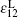
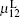
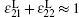
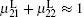
We have obtained the dispersion relationship of a probe wave propagating in a strong circular-polarized electromagnetic field with an arbitrary incident angle. Three special cases for θ = 0, π /2, π have been discussed in detail. The phase and direction dependence of the refractive index, the permittivity, and the permeability in the laboratory system have been obtained. The relationships have some symmetries. For the perpendicular incident probe wave with θ = π /2, there is only one permissible mode with the refractive index 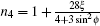. The negative refractive indices correspond to the counter propagating waves. With our results, it can be predicted that the probe wave experiences different refractive indices at different positions in the propagating path. Therefore, the polarization will be changed and the light path will be curved. With the phase dependence and the direction dependence, the polarization evolution and the practice curved path can be predicted in the strong electromagnetic circumstances of pulsar or neutron stars.

Until now, in the laboratory, the tightly focused strong circular-polarized laser pulse is the only way to generate the rotating electromagnetic field. However, if the probe wave is not propagating parallel to the focused pulse, the optical path is about several micrometers. Comparing the probe wave propagating through the strong field of the pulse and a probe wave with the same frequency propagating in a vacuum without any field, the phase shift of interference fringes, Δ ϕ _p, could be used to reveal the refractive index in the strong field. For a strong laser with an intensity of 10²⁰ W/cm², wavelength of 1 μ m and the probe wave with a wavelength of 1 μ m, we have | B_r| ≈ 10⁵ T and Δ ϕ _p ≈ 10^{− 13}. Therefore, it needs quite a precise measurement that we cannot realize currently.