†Corresponding author. E-mail: wangjin@wipm.ac.cn
*Project supported by the National Basic Research Program of China (Grant No. 2010CB832805) and the National Natural Science Foundation of China (Grant No. 11227803).
Development of atom interferometry and its application in precision measurement are reviewed in this paper. The principle, features and the implementation of atom interferometers are introduced, the recent progress of precision measurement with atom interferometry, including determination of gravitational constant and fine structure constant, measurement of gravity, gravity gradient and rotation, test of weak equivalence principle, proposal of gravitational wave detection, and measurement of quadratic Zeeman shift are reviewed in detail. Determination of gravitational redshift, new definition of kilogram, and measurement of weak force with atom interferometry are also briefly introduced.
Matter waves have similar interference behavior as light waves do, atom interferometers may be achieved by coherently manipulating atomic wave packet. There are four methods to manipulate an atomic wave packet: micro-structure grating, [1, 2] double-slit, [3, 4] stimulated Raman transition (SRT), [5] and laser standing wave grating.[6] Shimizu[4] achieved interference fringes of cold neon atoms using Young’ s double-slit. Laser standing wave gratings are easier to realize than artificial gratings, Bordé [7] proposed a method to experimentally display the interference characteristics of atoms via optical Ramsey oscillation. This proposal for atom interferometry (AI) experiment was realized by Riehle et al.[8] Laser field can be used to select internal state or external state of atoms for AI, Kasevich[5] achieved a cold atom interferometer by manipulating cold sodium atoms using two-photon SRT. The manipulating process includes several steps: preparation of atoms in initial state, splitting of atom cloud, evolution of atoms, combining of atomic wave packet, probe of internal state population, and extraction of external state information.
Due to the fast development of atom interferometers, precision measurements based on AI have also made great progress in recent years. AI can be used for measuring fundamental physics constants and parameters, such as gravitational constant, [9– 11] and fine structure constant.[12– 16] Atom interferometers are sensitive to the Earth’ s gravity field, they can be used for measuring absolute value and variation of gravitational acceleration, g; they can also be developed into atom gravimeters, [17– 19] atom gravity gradiometers, [20] to satisfy the application requirements of resource exploration, geophysical studies, seismic monitoring, and experimental test of basic physics laws.[21– 26] Due to Sagnac effects of interference loops, atom interferometers are inertial sensors, they can be made into high-precision atom gyroscopes, [27] and can be applied in aerospace, marine, earthquake prediction and automatic control. AI is one of the possible candidates for gravitational wave (GW) detection.[28– 31] AI based Compton clock provides a new benchmark for definition of kilogram.[25] Single atom interferometer can be used to measure weak force.[32]
In this paper, we introduce the principle, features and implementation of atom interferometers, review the latest progress of determination of fundamental physics constants, measurement of gravity, test of general relativity, measurement of rotation, proposal of GW detection, and other precision measurements with AI.
The most common atom interferometer is SRT-based cold atom interferometer. SRT process can be illustrated by a three-level atom model. As shown in Fig. 1, single-mode laser fields ω 13 and ω 23 couple two ground states | 1〉 , | 2〉 and an excited state | 3〉 , and cause a coherent SRT. Atomic population can be transferred among different ground states by SRT. This process is similar to the microwave Rabi oscillation between two ground states. Atoms in initial state | 1〉 transit to ground state | 2〉 by SRT process, and the population of state | 2〉 versus Raman beam intensity presents Rabi oscillation, [33, 34] which is a sine function.
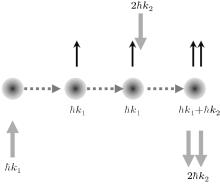
During the SRT process, the recoil momentum of atoms changes with the transference of population.[35] As shown in Fig. 2, photon momentum of counter-propagating Raman beams are ħ k1 and ħ k2, atom obtains recoil momentum, ħ k1, when it absorbs the first photon; atom obtains recoil momentum, ħ k2, when it absorbs the second photon; atom obtains recoil momentum, ħ k1 + ħ k2, when it emits two photons, 2ħ k2.
According to different Raman pulse sequence, cold atom interferometers can be classified as two basic types: Ramsey– Bordé (R– B) interferometer and Mach– Zender (M– Z) interferometer, other atom interferometers can be considered as the modification of these two types.
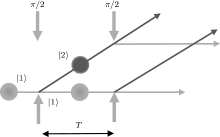
Ramsey interference spectroscopy was proposed in 1950.[36, 37] Bordé proposed Ramsey spectroscopy based R– B atom interferometer in 1989, [7] and R– B atom interferometer was demonstrated using dye laser and calcium atomic beam in 1991.[8] Atom R– B interferometer can be achieved by SRT using π /2– π /2 Raman pulse sequence. A typical experimental scheme of cold atom R– B interferometer is shown in Fig. 3. Cold atoms in initial state | 1〉 are split into states | 1〉 and | 2〉 when they interact with the first π /2-pulse, half of them stay in state | 1〉 , half of them transit to state | 2〉 , and all of the atoms freely move for a time of T, then interact with the second π /2-pulse. The dependence of population of atoms in state | 2〉 (or state | 1〉 ) on laser detuning shows R– B interference fringes.
Take rubidium R– B interferometer for instance, cold 85Rb atoms are first prepared in state 5S1/2, F = 2, then are operated by π /2– π /2 Raman pulse sequence. At the end of the first π /2-pulse, atoms are prepared in the coherent superposition state of two ground states 5S1/2, F = 2 and 5S1/2, F = 3. After free evolution time, T, the phase shift of the second π /2-pulse is scanned, and population of state 5S1/2, F = 2 or state 5S1/2, F = 3 are recorded to obtain R– B interference fringes.[38]
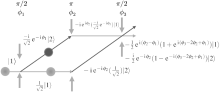
M– Z type atom interferometer[39] may be achieved by π /2– π – π /2 Raman pulse sequence. As shown in Fig. 4, atoms in initial state | 1〉 interact with the first π /2-pulse, and redistributed in state | 1〉 and state | 2〉 . Atoms in state | 2〉 obtain a phase shift of laser, ϕ 1, both atoms in state | 1〉 and state | 2〉 form a coherent superposition state 
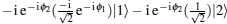
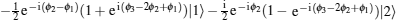
 | Fig. 5. Mach– Zender type interference fringe. The relative population depend on the voltage applied to the electro-optical modulator.[39] |
Determination of fundamental physics constants are important for basic theory, precision measurements, new definition of time units, further improvement of the accuracy of satellite positioning, etc. Fast development of AI in recent years, provides great convenience for measuring gravitational constant and fine structure constant, new progress in this area is of great inspiration.
The traditional tools to measure gravitational constant, G, are the torsion balances and precision balances, [41] both of them adopt macroscopic objects as testing quality. In 2003, Tino’ s group carried out the first measurement of G using AI.[42] The process of experimental measurement of G using an atom interferometer is summarized as follows. Two cold atom clouds, which are prepared in a same magneto-optical trap (MOT), are launched up vertically at different velocity in succession. Due to the gravity, the first atom cloud may fall with the same velocity as the second one, which was launched up at lower velocity. By this method, one can produce two atom clouds with similar parameters in top and bottom parts of an MOT chamber. Raman pulses for splitting, reflecting and combing atoms can be applied to two atom clouds simultaneously. The value of gravity gradient can be obtained by directly subtracting the phase shifts of two atom interferometers. Some well machined tungsten blocks are placed evenly around the device to modify gravity field near two atom clouds. G can be accurately measured by moving these tungsten blocks. Tino’ s group obtained the primary data of G using the above experimental methods in 2006 with a relative uncertainty of 0.01.[9] Kasevich’ s group reported a new result of G measured by AI in 2007, [10] they used two atom interferometers to measure the gravity gradient, [20] two atom interferometers are vertically separated. A lead block, which can be moved vertically, is used to change gravity field around these two interferometers. The relative uncertainty of measured value of G is 4.0× 10− 3. Tino’ s group improved experimental measurement of G in 2008, the relative statistic uncertainty is 1.6× 10− 3, and the relative systematic uncertainty is 4.5× 10− 4, [43] they modified the atom preparation system, measurement system and Raman beam in 2010, [44] improved the signal to noise ration and long-term stability. The relative uncertainty of measurement realized in 2014 is 1.5× 10− 4.[11]
Fine structure constant, α , is usually measured by fine structure splitting of atoms, [45] quantum Hall effect, [46] and electron anomalous magnetic moment.[47] The recommended value of α in CODATA-2010 is 1/137.035999074, and the relative uncertainty of this value is 3.2× 10− 10.[48] In recent years, a new method for determination of α based on AI is developed, one can indirectly measure the ratio of Planck constant and atomic mass, h/m, using AI, and then extract the value of α by h/m. The calculation formula for α can be expressed with h/m as

where c is the speed of light in vacuum, mp is the mass of proton, and me is the mass of electron. As long as the value of h/m is measured, the value of α can be obtained. Interference process of atoms depends on the momentum exchange between light and atoms, the recoil velocity of atoms, υ r, during interference process can be measured by AI. Recoil velocity is proportional to h/m, that is υ r = (h/m)(k/2π ). Thus h/m can be determined by υ r using AI.
In 1994, Chu’ s group measured the ratio of Planck constant and mass of cesium atoms, h/mCs, using a cesium atom interferometer, they thus obtained the value of α . The measurement uncertainty is 1× 10− 7, [12] which is the first measurement of α using AI. They improved their experiment and measured the value of α with relative uncertainty of 7.4× 10− 9[13] in 2002. Clade et al. measured fine structure constant using a rubidium atom interferometer with a relative uncertainty of 6.7× 10− 9 in 2006.[14] Cadoret et al. improved the accuracy of the measurement of α to 4.6× 10− 9 in 2008.[15] Bouchendira et al.[16] measured α using an atom interferometer with an uncertainty of 6.6× 10− 10 in 2011.
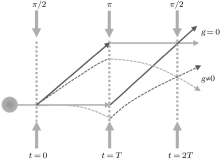
Atom interferometers are new type gravity measuring instruments. The information of gravity field, which influence on atom interference process, can be extracted by phase shift of the interference fringes. The principle of atom gravimeters can be simply described as Fig. 6, if atom clouds do not suffer any external gravity (g = 0), the interference loop will be a parallelogram as solid line in Fig. 6, there is no path difference between two atom clouds, the phase shift of interference fringes is zero. While, if the gravity field is considered (g ≠ 0), the interference paths of atom clouds will follow the parabolic trajectory (dash line in Fig. 6). The final phase shift of interference fringes in gravity field, Δ ϕ , can be described as

where keff is the effective wave vector of Raman beams, and T is the time interval between Raman pulses. According to Eq. (2), the phase shifts of atom interference fringes depend on g, keff, and T. While keff and T can be accurately controlled by the time-frequency technology. When the phase shift, Δ ϕ , is measured, it is possible to achieve precision measurement of the absolute value of g.
Kasevich et al.[6] experimentally demonstrated gravity measurement using a laser-cooled sodium atom interferometer in 1991, the resolution of their measurement is Δ g/g = 3× 10− 6; their improved measurement resolution in 1992 is Δ g/g = 3× 10− 8.[49] Peters et al.[18] reported a precision measurement of g with a resolution of Δ g/g = 1× 10− 10 using a cesium interferometer in 2001. Zhou et al.[19] demonstrated local gravity measurement and solid tide observation using a compact cold rubidium atom gravimeter in 2011. The solid tidal data of the Earth are shown in Fig. 7, the dotted line is experimental data, and the solid line is calculation curve according to the theoretical model. If the chirp rate equals the Doppler shift due to the gravity, the gravitational phase shift of interference fringes exactly compensates the phase shift of Raman beams. The short-term sensitivity of the atom gravimeter evaluated using Allan variance[50] is 
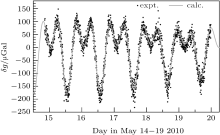 | Fig. 7. Gravity data measured at Wuhan during May 14– 19, 2010.[19] |
Ultracold degenerate gases are good candidates for atom gravimeters due to their obvious wave characteristic. Roati et al.[51] used degenerate Fermi gases in gravity measurement in 2004; Debs et al.[52] measured gravity using interference information of rubidium Bose– Einstein condensate (BEC) in 2011. However, compared with fountain type cold atom gravimeters, the equipment and the experimental process of gravimeters using degenerate Fermi gases or BECs are too complicated to actual application.
Usually, Raman pulse sequence, π /2– π – π /2, are used to manipulate atoms to form an interference loop in a fountain type cold atom gravimeter. In this case, atoms in different paths are in different internal states, frequency shifts due to the fluctuation of magnetic field and light field are important sources of noise and syetematic errors. To solve these problems, Malossi et al.[53] demonstrated an AI scheme based on double-Raman transition in 2010. Fray et al.[21] manipulated atoms to interfere using Bragg diffraction in 2004, and obtained atom interference fringes by detecting external states of atoms. Altin et al.[54] demonstrated an atom gravimeter based on Bragg diffraction in 2013, and the measurement resolution is Δ g/g = 2.7× 10− 9.
It is interesting to compare the capabilities of atom gravimeters with classical ones. Merlet et al.[55] comparatively investigated the capabilities of an atom gravimeter and a traditional absolute gravimeter in 2010, the measurement accuracies of two types of gravimeters coincide with each other at the level of (4.3 ± 6.4) μ Gal (1 μ Gal ≃ 10− 9 g). Poli et al.[56] carried out a similar experiment using a cold atom gravimeter and a traditional gravimeter in 2011. Although the capability of atom gravimeters is on a par with a classical gravimeters at present time, there is great potential to improve the accuracy, the sensitivity and the resolution of an atom gravimeter by technical innovation. Kasevich’ s group improved the resolution of an atom gravimeter by extending the interval time in 2013, [57] they achieved a resolution of Δ g/g = 6.7× 10− 12 under the condition of T = 1.15 s; Hu et al.[58] improved the short-term sensitivity of an atom gravimeter to 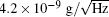
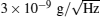
An atom gravimeter has a higher sensitivity, but its system structure is too complex, and its technology is too sophisticated. The key problem of actual application of atom gravimeters is how to make the system miniature and robust. In 2008, Le Gouë t et al.[60] improved the sample rate by shorting the interval time of Raman pulses, realized a compact atom gravimeter with a short-term resolution of Δ g/g = 1.4× 10− 8. Landragin’ s group[61, 62] demonstrated a one-laser-beam cold atom gravimeter in 2010, the short-term resolution is Δ g/g = 1.7× 10− 7 at integration time of 1 s. Butts et al.[63] demonstrated an atom gravimeter with millisecond interrogation times in 2011. McGuinness et al.[64] demonstrated a high data-rate atom gravimeter which is optimized to operate at rates up to 330 Hz with a sensitivity of 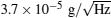
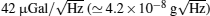
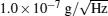
Gravity gradient can be determined by differentially measuring the gravities of two different sites. The accuracy of gravity gradient measurement depends on the capability of a gravity gradiometer. In absolute gravity measurements, vibrational noise is the main source which limits the sensitivity and the accuracy of a gravimeter. While in gravity gradient measurements, sensitivity can be greatly improved by reducing vibrational noise using common-mode rejection technology.
Kasevich’ s group[20] achieved common-mode differential measurement of absolute gravity using two vertical stacked atom gravimeters in 1998, and demonstrated the first measurement of gravity gradient tensor using AI; they optimized the experimental parameters in 2002, and achieved differential measurement of gravity with a sensitivity of 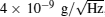


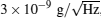

Equivalence principle (EP) is one of the basic assumptions of Einstein’ s general relativity. EP includes the universality of free fall (UFF) which known as weak equivalence principle (WEP), the local Lorentz invariance (LLI) and the local position invariance (LPI). Some theories predicted that there should be new interaction forces which depend on size, materials, speed, and position of objects. In other words, the EP will be broken in some extent, and the precision tests of EP have scientific significance.
There are plenty of EP test experiments using macroscopic objects, but no experiments were found to break the EP until now. What will happen if we use microscopic particles in EP test experiments? The motion of microscopic particles needs to be described by quantum mechanics rather than by Newtonian mechanics, so there should be some conceptual problems in free fall experiments using microscopic particles.[73] Since 1960s, free-falling microscopic particles in gravity field have been studied theoretically and experimentally.
The difference between gravitational accelerations of two objects, which is due to different materials, is a key parameter in the WEP test experiments. Assuming that a1, 2 are gravitational accelerations of two objects, mg is the gravitational mass, mi is the inertial mass, and the relative difference of gravitational acceleration of two objects can be described as[73]
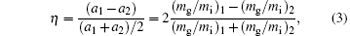
where η is called Eö tvö s factor. If WEP holds, then mg = mi, η = 0; otherwise, η ≠ 0. Take 85Rb and 87Rb for instance, the accuracy, η , of WEP test depends on the measurement accuracy of gravitational acceleration of each isotope atoms. The Eö tvö s factor can be expressed as
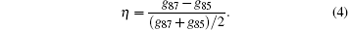
Traditional WEP tests include torsion balance experiments, [74] drop tower experiments, [75] lunar laser ranging experiments, [76] and macroscopic gyros experiments.[77– 79] There are few WEP test experiments using microscopic particles, and neutrons were used to test the WEP[80, 81] with a poor accuracy. Development of AI provides a new way for the WEP test using microscopic particles.[82] Compared with neutrons, cold atom interferometers can be used to test WEP with higher precision due to lower velocity and better coherence of cold atoms. Theoretical analysis showed that the precision of WEP test experiments using atom interferometers is expected to reach 10− 15.[83]
A group in Max– Planck Institute for Quantum Optics completed the first WEP test experiment based on atom interferometers in 2004.[21] They used moving molasses to form 85Rb and 87Rb fountains, and used Bragg diffraction to achieve external state interference. The test accuracy is (1.2± 1.7) × 10− 7. A group in French Aerospace Laboratory tested WEP using free-falling 85Rb and 87Rb atoms in 2013 with an accuracy of (1.2 ± 3.2) × 10− 7.[22] In 2014, Rasel’ s group in Leibniz University demonstrated WEP test using 87Rb and 39K atom interferometers with an accuracy of (0.3 ± 5.4) × 10− 7; [23] Tino’ s group demonstrated WEP test using bosonic and fermionic isotopes of strontium atoms with an accuracy of (0.2 ± 1.6) × 10− 7.[24] In addition, Mü ller is actively planning a WEP test experiment using cesium and lithium atoms, and is building a lithium atom interferometer.[84]
The sensitivity of an atom interferometer depends on the free evolution time of atoms. To increase the free evolution time, it is necessary to develop large-scale atom interferometers. Kasevich’ s group demonstrated a light-pulse atom interferometer with a duration of 2.3 s, and the inferred sensitivity is 6.7× 10− 12 g.[57] They further enhanced the readout of the 10-meter atom interferometer by a phase shear method.[85] Zhan’ s group designed and developed a 10-meter-fountain type atom interferometer[50] for the WEP test experiment, the schematic diagram of 10-meter atom interferometer is shown in Fig. 8. The maximum fountain height is 12.3 m, and the main part of the interferometer includes the bottom MOT, the vacuum tube, and the top MOT. The bottom MOT is used to prepare 85Rb– 87Rb fountains; the top MOT is used to prepare free falling clouds of rubidium and lithium atoms; Zeeman slowers are used to supply atom source for MOTs. Based on this setup, dual-MOT of 85Rb– 87Rb has been achieved, [86] and dual-species fountain signal and interference fringes using double-Raman transition are observed. In addition, Chen et al.[87] proposed a new data processing method to suppress the vibrational noise in non-isotope dual-atom-interferometer-based WEP test experiments, Tang et al.[88] designed and demonstrated a compact stable active low-frequency vibration isolation system for decreasing the vibrational noise in AI caused by the reflecting mirror of Raman beams.
Another application of AI in fundamental physics is to determine gravitational redshift. Mü ller et al.[25, 26] analyzed the previous experimental results of gravity measurements using atom interferometers. They considered that the gravitational redshift can be measured by atom interferometers, and the experimental data are consistent with the theoretical prediction at the level of 7 × 10− 9. This precision is four orders of magnitude better than similar experiments using atom clocks. The publication of this result caused some controversies.[89– 92] In order to solve the dispute of redshift, Schleich et al. proposed Kasevich– Chu interferometer scheme[93] based on operator algebra. This interferometer is an accelerometer or a gravimeter.
The Sagnac effect of a light interference loop is the basis of laser gyros and optical fiber gyros. Atom interference loop can also be used as gyros to measure the rotation.[27] Bordé et al.[8] firstly demonstrated the Sagnac effect of a calcium atomic beam R– B interferometer, which was achieved by four standing laser fields. Due to lower velocity and longer wavelength of matter waves, AI-based gyros are more sensitive than laser gyros.[94] The principle of M– Z type atom gyros is shown in Fig. 9.
When an atom interferometer is placed in a frame with rotation rate, Ω , the phase shift of interference loop caused by rotation is
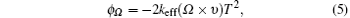
where υ is the velocity of atoms. According to the status of atoms involved in interferometers, atom gyros can be classified into four types: thermal atomic beam gyros, cold atoms gyros, chip-based atom gyros, and quantum vortex gyros. The sensitivity of atom gyros, also known as angle random walk (ARW), depends on two parameters: atom number and scaling factor. The more atoms there are, the better the sensitivity is; the bigger the scaling factor is, the better the sensitivity is.
Thermal atomic beam gyros have better sensitivity, better long-term stability, and broad bandwidth due to more atoms and bigger scale factor. Pritchard’ s group[95] demonstrated the Sagnac effect of an atomic beam interferometer and measured the rotation rate of the Earth in 1997. Kasevich’ s group[96] realized an atomic beam gyro by SRT, with the short-term ARW being 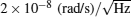

Although the sensitivity of a thermal atomic beam gyro is better, its volume is too large for practical applications. A feasible way to solve this problem is to shorten interference area by substituting thermal atomic beam with cold atoms. Canue et al.[99] designed and achieved a cold atom gyro using two counter-propagating cold-atom clouds in 2006, with the bias stability being 2.2 × 10− 6 rad/s, and 10-minutes integral bias stability being 1.4 × 10− 7 rad/s. Mü ller et al.[100] generated a high-flux (1010 atoms/s) atomic beam for cold atom gyro in 2007, and they demonstrated a compact dual-loop cold atom gyro in 2009.[101] Tackmann et al.[102] achieved a small cold atom gyro with self-collimation large loop area in 2012, and the ARW is 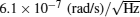

Ultracold atoms or BECs can be guided to achieve a spatial interference loop for rotation measurement. Shin et al.[104] realized an atom interferometer using BECs in a double well. Tolstikhin et al.[105] demonstrated the Sagnac effect of a matter wave interferometer using cigar-shaped BECs. Wu et al.[106] implemented an atom gyro based on mobile waveguides. They identified the rotation signal which is 10 times of the Earth’ s rotation rate. Baker et al.[107] designed a chip-based ring trap which can be used to guide cold atoms, molecules, or BECs to form gyros. Debs et al.[108] studied the characteristics of BECs using three different output couplers. Yan[109] proposed an idea to achieve close-loop atom interferometers on a chip using a moveable waveguide, and atoms can be split and combined by a moveable microwave waveguide.
Vortex characteristics of superfluid may also be used to measure the rotation. Stringari[110] proposed a vision of rotation measurement based on quantum vortex characteristic of BECs. Hodby[111] observed three-dimensional Sagnac effect in BECs. Avenel et al.[112] demonstrated a gyro based on Josephson effect of superfluid 3He and 4He. Narayana et al.[113] demonstrated the Sagnac effect of superfluids. Thanvanthri et al.[114] proposed a scheme of atom gyro using vortex superposition state of BECs.
The existence of GW was predicted by Einstein in 1916, but there are only few GW observation results till now.[115– 117] Research on the GW detection using matter wave interferometers started in 1979, [118] and more and more attention has been paid to this method since AI was applied in precision measurement. In 2004, Chiao et al.[119] studied and found that matter-wave interferometer gravitational wave observatory (MIGO) will be more sensitive than laser interferometer detectors, while Roura et al.[120] questioned their conclusions. In 2007, Tino and Vetrano[121] carefully analyzed the scheme of MIGO, they considered that short-baseline MIGO can detect low-frequency GW with a sensitivity comparable to large-baseline laser interferometers. Wicht et al.[122] proposed a solution to GW detection based on internal state interference of molecule in 2008. Dimopoulos et al.[28] proposed a space-based atom interferometer GW detector in 2009, and its expected strain sensitivity is 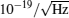
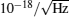
Although the optimal scheme and the practical experimental details of matter-wave interferometer GW detectors are not very clear, AI provides us a possible breakthrough in the GW detection.
In addition to measuring gravity and rotation, the phase of atom interference fringes is also very sensitive to external magnetic field. The quadratic Zeeman shift of certain transition of atoms can be measured precisely by an atom interferometer. The transition between insensitive magnetic sublevels is usually called “ clock transition” in atom fountain clocks, precision measurement of quadratic Zeeman shift of clock transition is very important for atom frequency standards and other high-resolution spectroscopy experiments. Li et al.[40] measured the quadratic Zeeman shift of clock transition of 85Rb using an atom interferometer in 2009. The quadratic Zeeman shift is determined by measuring the resonance frequencies of coherent population transition in Raman transition process. The frequency shifts of the transitions 5P1/2, F = 2, mF = − 2 → 5P1/2, F = 3, mF = − 2 and 5P1/2, F = 2, mF = 2 → 5P1/2, F = 3, mF = 2 of 85Rb are measured as a function of magnetic field, and the intensity of magnetic field is proportional to the current applied to magnetic coils. The scale factor of the magnetic field is 1576.9 ± 1.3 mG/A. The dependence of transition probability of the ground-state clock transition on two-photon detuning, is determined by applying bias magnetic field along the direction of Raman beams. The coefficient of quadratic term corresponding to the quadratic Zeeman shift of clock transition is 1296.8 Hz/G2. The error caused by scaling the magnetic field is 2.1 Hz/G2, and the error caused by the fitting is 2.5 Hz/G2. Wu et al.[129] measured the quadratic Zeeman coefficient of 87Rb clock transition by using the Ramsey atom interferometer with an uncertainty of less than 1 Hz/G2, and they experimentally verified the Breit– Rabi formula.[130] Zhou et al.[131] measured magnetic field gradient with an atom interferometer, the resolution of 90-s integration time is 300 pT/mm. Hu et al.[132] demonstrated a differential method to reject the common-mode noise and to improve the measurement resolution of magnetic field gradient by two simultaneously operated atom interferometers.
It is possible to redefine the kilogram by AI. In 2010, Mü ller et al.[25] proposed that atoms involved in atom interferometers can be considered as clocks running at Compton frequency, ω c. ω c is relevant to the rest mass of atoms: ω c = mc2/ħ , that is, the unit of quality can be defined by Compton frequency. Wolf et al.[89, 133] doubt this scenario. They believed that, Compton phase difference between two atom interference paths is zero in the framework of general relativity and other theories. Thus, gravitational redshift cannot be tested using AI-based Compton frequency unless the Schiff conjecture and other physics laws are violated. Mü ller[90] responded that Wolf et al. misused Schiff conjecture when they reached their conclusion, and gravitational redshift effect can be directly tested by atom interferometers. In 2013, Mü ller et al.[134] experimentally demonstrated a Compton clock. They calibrated an atom interferometer using an optical frequency comb, synchronized the oscillator by pulse spectrum of recoil atoms, and directly linked the mass of the particle to the time. In short, Compton clock can be used to measure “ kilogram” with “ seconds” .[135]
The capability of atom interferometers in measurement of gravity can be used to test Newton’ s inverse square law at medium or short distance.[136] Lepoutre et al.[137] measured the phase shift caused by atom– surface van der Waals interaction using AI. Since the collective interference effect of single atoms is equivalent to interference of atom cloud, single-atom interferometers can be used for measuring weak force. Preparation of single atoms in optical dipole trap is the precondition for achieving a single-atom interferometer. The first single-atom trap is demonstrated by Frese et al.[138] in 2000. Zhan’ s group has achieved optical bottle trap, [139] hybrid red-blue detuned optical trap, [140] and phase decoherence suppression[141] of single atoms. Parazzoli et al.[142] observed interference of matter waves using free falling single atoms, and demonstrated the weak force measurement by a single-atom interferometer in 2012. They directly detected the velocity distribution of free falling single atoms, and measured the temperature of single atoms using coherence length of atomic wave packet. The single-atom interferometer can detect the force of 3.2× 10− 27 N level with spatial resolution of micrometer scale. This sensitivity can be used to measure Casimir– Polder potential.
Development of AI provide experimental techniques for precision measurements based on atomic and molecular physics. Traditional precision measurements, such as determination of gravitational constant, measurement of fine structure constant, test of weak equivalence principle, and detection of gravitational wave, will benefit from the AI, deepen our understanding of general relativity and the origin of the universe. Principle demonstration, technology development and practical application of atom gravimeters, atom gravity gradiometers and atom gyros, will fully exert the advantages of AI. Precision measurement with AI is a new cross field which is full of vigor and vitality, and it is worth our attention.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|
| 55 |
|
| 56 |
|
| 57 |
|
| 58 |
|
| 59 |
|
| 60 |
|
| 61 |
|
| 62 |
|
| 63 |
|
| 64 |
|
| 65 |
|
| 66 |
|
| 67 |
|
| 68 |
|
| 69 |
|
| 70 |
|
| 71 |
|
| 72 |
|
| 73 |
|
| 74 |
|
| 75 |
|
| 76 |
|
| 77 |
|
| 78 |
|
| 79 |
|
| 80 |
|
| 81 |
|
| 82 |
|
| 83 |
|
| 84 |
|
| 85 |
|
| 86 |
|
| 87 |
|
| 88 |
|
| 89 |
|
| 90 |
|
| 91 |
|
| 92 |
|
| 93 |
|
| 94 |
|
| 95 |
|
| 96 |
|
| 97 |
|
| 98 |
|
| 99 |
|
| 100 |
|
| 101 |
|
| 102 |
|
| 103 |
|
| 104 |
|
| 105 |
|
| 106 |
|
| 107 |
|
| 108 |
|
| 109 |
|
| 110 |
|
| 111 |
|
| 112 |
|
| 113 |
|
| 114 |
|
| 115 |
|
| 116 |
|
| 117 |
|
| 118 |
|
| 119 |
|
| 120 |
|
| 121 |
|
| 122 |
|
| 123 |
|
| 124 |
|
| 125 |
|
| 126 |
|
| 127 |
|
| 128 |
|
| 129 |
|
| 130 |
|
| 131 |
|
| 132 |
|
| 133 |
|
| 134 |
|
| 135 |
|
| 136 |
|
| 137 |
|
| 138 |
|
| 139 |
|
| 140 |
|
| 141 |
|
| 142 |
|