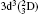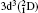Cite this Article
Aggarwal Sunny, Jha A. K. S., Khatri Indu, Singh Narendra, Mohan Man. Relativistic atomic data for W XLVII. Chinese Physics B, 2015, 24(5): 053201  
Permissions
Relativistic atomic data for W XLVII
Aggarwal Sunnya),b)†, Jha A. K. S.a), Khatri Indua), Singh Narendrab), Mohan Mana)
Department of Physics and Astrophysics, University of Delhi, Delhi, India
Department of Physics, Shyamlal College, University of Delhi, Delhi, India

†Corresponding author. E-mail: sunny.kmc87@gmail.com

Abstract

Energy levels, radiative rates, and lifetimes are calculated for all levels of 3s23p, 3s23d, 3s3p2, 3s3d2, 3s3p3d, 3p23d, 3s3d2, 3p3d2, 3p3, and 3d3 configurations of Al-like tungsten ion (W XLVII). Multiconfigurational Dirac–Fock (MCDF) method is adopted for calculating energy levels and radiative rates. Oscillator strengths, radiative rates, and line strengths are reported for some E1 transitions from the ground level. Comparisons are made with the available data in the literature and good agreement has been found which confirms the reliability of our results.

Keyword: 32.70.Cs; atomic data; multiconfigurational Dirac–Fock method; transition probability
1. Introduction

Spectroscopic parameters of tungsten ions are essential for exploring the physical conditions in tokamak plasmas such as ITER in which tungsten is currently considered to be a promising candidate for the plasma-facing material in the divertor region.[1] As sputtering at the surfaces with plasma contact cannot be avoided completely, tungsten will be an intrinsic impurity in these plasmas. The electron temperatures in ITER will range from below 0.1  keV at the edge up to about 30  keV in the core of the plasma. The measured spectra often contain many spectral lines from several ionization stages forming spectral features. To understand its influence as a plasma impurity, reliable atomic data are needed for many ionic stages of tungsten.

Many investigations have been carried out for the Al-like tungsten in the last two decades both theoretically as well as experimentally. For instance, on the theoretical side, Feng et al.[2] have presented a comprehensive study of atomic characteristics of ten tungsten ions including W XLVII in a broad range of wavelengths, energy levels and transition probabilities. They have also presented results of multiconfiguration Dirac– Fock and relativistic configuration interaction calculations including the Breit interaction. Safronova and Safronova[3] have calculated the excitation energies for Al-like W61+ of the [2p6]3s23p, 3s3p2, 3d23d, 3s3p3d, and 3p3 levels and radiative rates of the E1 transitions between them. Further, Huang[4] has tabulated transition rates and oscillator strengths for Al-like ions, calculated by the multiconfiguration Dirac– Fock (MCDF) method. Relativistic many-body calculations of electric dipole lifetimes, transition rates and oscillator strengths for n = 3 states in Al-like ions were presented by Safronova et al.[5] They calculated the transition rates, oscillator strengths, and line strengths for electric-dipole (E1) transitions between even-parity 3s3p2, 3s23d, 3p23d, 3d23s, and 3d3 states and odd-parity 3s23p, 3p3, 3s3p3d, and 3d23p states in Al-like ions with the nuclear charges ranging from Z = 15 to 100.[5] Further, Lavin et al.[6] have reported oscillator strengths corresponding to dipole-allowed transitions for a group of Al-like ions (Z = 13– 103).

On the experimental side, Ralchenko et al.[7] reported the measurements of extreme ultraviolet (EUV) spectra (4– 20  nm) of highly-charged tungsten ions W54+ to W63+ obtained with an electron beam ion trap (EBIT) facility at the National Institute of Standards and Technology (NIST). The three levels 2P1/2, 2P3/2 of 3s23p, and 4P1/2 of 3s3p2 of Al-like tungsten were found using EBIT at NIST.

The aim of this work is to upgrade the database of energy levels, oscillator strengths, transition probabilities, and lifetimes of Al-like tungsten ion. The investigations of highly charged Al-like tungsten ion considered in the present work require the simultaneous consideration of electronic correlation and relativistic effects. For this purpose, we use MCDF technology which was originally developed by Grant et al.[8] and revised by Norrington.[9] It includes the most important configuration effects as well as quantum electrodynamics (QED) correction and has been applied successfully to calculate atomic data for highly charged ions.[10– 18] In our calculations, all the orbitals are simultaneously optimized on the average energy of all configurations by using the option of EAL (extended average level).

The rest of this paper is organized as follows. In Section  2, we present the method of calculations, then the energy levels and wavefunction compositions are presented in Section 3. In Section 4, we report the radiative rates for electric dipole (E1) and magnetic quadrupole (M2) transition. In Section 5, we present the lifetimes of excited states. Finally, the conclusion is given in Section 6.

2. Calculation method

We obtain results using the multiconfiguration Dirac– Fock method employed in the GRASP code of Grant et al., [8] revised by Norrington[9] and recently used by various authors.[10– 18] In the MCDF approach, the Hamiltonian for an N-electron atom or ion Dirac– Coulomb Hamiltonian is given by

where

is the single particle Hamiltonian consisting of kinetic energy and its interaction with the nucleus. In Eq.  (1), α and β represent 4× 4 Dirac matrices where c is the speed of light. The N-electron wavefunction is constructed from central-field Dirac orbitals given by

where k is the Dirac angular quantum number, k = ± (j + 1/2) for l = j ± 1/2, so j = k − 1/2, m is the projection of the angular momentum j, and Pnk and Qnk are radial functions. The spin angular momentum χ km(θ , ϕ ) is a 2 component function defined by

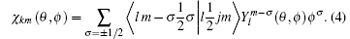
An atomic state function (ASF) can now be formed for an N-electron system with the given total angular momentum J, M and parity P is approximated by a linear combination of nc electronic configuration state functions (CSFs)

where nc is the number of CSFs included in the expansion, Ci(α ) are the expansion mixing co-efficients, and α represents all information such as orbital occupation numbers, coupling, etc. The CSFs are usually chosen to be orthonormal, so that

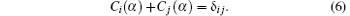
For expectation of the Dirac– Hamiltonian, we get the energy of the N-electron system as

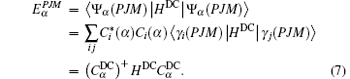
The Hamiltonian matrix, HDC has elements

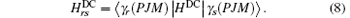
Using the normalization condition

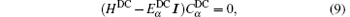
where I is the nc × nc unit matrix. Thus the predicted atomic energy level 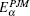can be taken to be eigenvalues of HDC. In the present calculation, QED corrections (including vacuum polarization and self energy), are considered in the first order of perturbation theory. One-electron excitations from 3s and 3p orbitals of 3s23p configuration as well as two electron excitations from orbitals with n = 3 to all possible combinations of one or two electrons in the shells up to n = 4 were employed to generate one-electron wavefunctions as a basis set for CSFs in the MCDF method. Therefore, we use [1s22s22p6] 3s23p, 3p3, 3p3d2, 3p4s2, 3p4f2, 3p4d2, 3s24p, 3s24f, 3p24p, 3p24f, 3s3p2, 3s23d, 3p23d, 3s3d2, 3d3, 3s24s, 3d4s2, 3d4p2, 3d4d2, 3d4f2, 3s 24d, 3p24s, 3s3p3d, 3s3p4s, 3s3p4p, 3s3p4d, 3s3p4f, 3s3d4s, 3s3d4p, 3s3d4d, 3s3d4f, 3p3d4s, 3p3d4p, 3p3d4d, and 3p3d4f configurations. We also present a detailed comparison of our theoretical calculations with the data recommended from the NIST database.

3. Energy levels

We have performed calculations on transitions energies for the 148 fine structural levels belong to 3s23p, 3s23d, 3s3p2, 3s3d2, 3s3p3d, 3p23d, 3s3d2, 3p3d2, 3p3, and 3d3 configurations of Al-like tungsten. The Ne-like (1s22s22p6) core was treated as an inactive core. Energy levels of all the fine structural levels generated by above configurations have been calculated by the fully relativistic Multiconfigurational Dirac– Fock method. The flexible atomic code (FAC), which is also fully relativistic and based on the j j-coupling scheme has been used to generate all relevant atomic data.

The energy levels with their labels obtained using MCDF and FAC lifetimes of excited levels for Al-like tungsten are presented in Table  1. The calculation includes ([1s22s22p6]3s23p, 3p3, 3p3d2, 3p4s2, 3p4f2, 3p4d2, 3s24p, 3s24f, 3p24p, 3p24f, 3s3p2, 3s23d, 3p23d, 3s3d2, 3d3, 3s24s, 3d4s2, 3d4p2, 3d4d2, 3d4f2, 3s 24d, 3p24s, 3s3p3d, 3s3p4s, 3s3p4p, 3s3p4d, 3s3p4f, 3s3d4s, 3s3d4p, 3s3d4d, 3s3d4f, 3p3d4s, 3p3d4p, 3p3d4d, and 3p3d4f) configurations, which generate 894 energy levels, of which 148 are listed in Table  1. As QED corrections are important for transition energy calculations, therefore we present the QED corrections in our results. Further, we show the contributions to the excitation energies arising from different parts of the Hamiltonian and compare our level energies calculated by MCDF (included Breit and QED effects) with the FAC.

Table 1. Dirac– Coulomb (DC), Breit, and quantum electrodynamics (QED) contributions to the MCDF energy (in Rydberg) as a function of the orbital set. The sum (total) is compared with FAC. All energies are relative to the ground state.

In Table  1, we report many new spectral lines which have not been reported either experimentally or theoretically. Energy values for 13 fine structure levels were compiled by NIST. We present energy values for the fine structural levels belonging to 3s3d2, 3p3d2, and 3d3 configurations, which are reported for the first time. We also present new results for many levels belonging to 3p3, 3p23d, and 3s3p3d configurations.

In Table  2, we compare our calculated results for energy values from MCDF and FAC with the energy levels compiled by NIST, which are based on the data listed by Kramida.[19] The experimental energy values compiled by NIST were measured by some authors.[3, 7, 20– 22] In Table  2, we also present the calculated values of Safronova.[3] For the levels belonging to 3s23p, 3p23d, and 3s23d configurations, our calculated energy values with MCDF are in good agreement with the NIST values and other theoretical results.[3] For the level 3s3p2, our energy values calculated with MCDF agree well (error 0.2– 1.1%) with NIST values. The disagreement between our calculated MCDF energies and FAC energies of the 3s3p2 level is about (0.06– 0.23%) except for the level 3s3p2 (4P1/2) (level 2) for which both calculated results differ by 1%. Further, the calculated energies for the levels 3p3 and 3s3p3d by the MCDF method agree well with those calculated by FAC and Safronova.[3] The maximum disagreement between MCDF and FAC results for these levels is 0.36% while between MCDF and results of Safronova[3] is 0.49%. Further, the ordering of Safronova and our calculated results is the same. In our MCDF calculation, we include those configurations which can provide reliable energy levels and whose energy levels interact with other energy levels. Therefore, we conclude that our MCDF results agree well with other available experimental and theoretical results.

Table 2. Energy level (in Rydberg) for the lowest 40 levels compared with other available results.
4. Radiative rates

In Table  3, we present the transition wavelengths (λ in Å ), radiative rates (Aji in s− 1, oscillator strengths (fi j, dimensionless), and line strengths (S in a.u. (atomic units)), in length form only, for electric dipole (E1), electric quadrupole (E2), magnetic dipole (M1), and magnetic quadrupole (M2) transitions from the ground state (3s23p 2P3/2) of Al-like W. To show the reliability of our results, in Table  4, we report the transition wavelengths for some levels and compare them with the available experimental and theoretical work. One can see from Table  4 that our transition wavelengths calculated with MCDF are in reasonable agreement with other theoretical and experimental results. For 3s23p 2P1/2− 3s3p24P1/2 transition, our results differ 1.1% from the experimental transition wavelength, while the theoretical results of Pü tterich et al.[23] differ by 1.8% from experimental results. For all other transitions, our transition wavelength agrees within an error range of 0.02− 0.4%. In addition, the mean ratio λ This work/λ exp. is found to be 0.9943. This is a clear indication of the accuracy of our calculated results.

Table 3. Transition data for E1, E2, M1, and M2 transitions from 3s23p 2P3/2: levels and 2J for lower level i, upper level k, wavelength λ (in Å ), line strength S (length form), oscillator strength f (length form), transition rate Aji (length form) calculated using MCDF.
Table 4. Comparison of computed wavelengths (in Å ) from different theories with observed wavelengths for transitions from 3s23p 2P1/2 to selected upper levels.

In Table  5, we compare our calculated transition probabilities for some transitions with other theoretical results. For 3s23p 2P1/2− 3s3p24P1/2 transition, the results of Pü tterich et al.[23] differ by an order of magnitude from the results of Ralchenko et al.[7] as well as other theoretical results. Our calculated transition probability agrees well (within 1%) with Ralchenko et al.[7] for the 3s23p 2P1/2− 3s3p24P1/2 transition. The A-value calculated by Quinet[10] differs by an order of magnitude with all available theoretical results. From Table  5, it can be seen that our calculated value of transition probabilities are in good agreement with the other available results for all transitions.

Table 5. Comparison of computed transition probabilities (in s− 1) from different theories for transitions from 3s23p 2P1/2 to selected upper levels.

Our calculated oscillator strength using MCDF for some transitions with other theoretical results are compared in Table  6. For the transition 3s23p 2P1/2− 3s23d 2D3/2, we compare our results with the results of Lavin et al.[6] who calculated f-values using three different approaches (QDO, RQDO, and MCDF-EAL). From Table  6, it can be seen that our MCDF f-values for the 3s23p 2P1/2− 3s23d 2D3/2 transition is in close agreement with their MCDF-EAL results.[6] For the 3s23p 2P1/2− 3s23p 2P3/2 transition, the maximum disagreement between our calculated f-value and the other available f-value is about 5%. It shows that our results are quite reliable.

Table 6. Comparison of computed oscillator strengths from different theories for transitions from 3s23p 2P1/2 to selected upper levels.
5. Lifetimes

The lifetime (τ ) for a level j is defined as

Calculations for transition probabilities have become advanced and require relativistic effects to be included. All possible E1 (electric dipole), E2 (electric quadrupole), M1 (magnetic dipole), and M2 (magnetic quadrupole) transitions are computed from which the lifetimes of levels have been determined. To the best of our knowledge, no calculations or measurements are available in the literature for lifetimes in Al-like tungsten. We hope that our calculated values of lifetimes will be beneficial to experimentalists in their future work.

6. Conclusion

In this paper, we have presented the energies of 3s23p, 3s23d, 3s3p2, 3s3d2, 3s3p3d, 3p23d, 3s3d2, 3p3d2, 3p3, and 3d3 configurations of Al-like tungsten ion (W XLVII) levels and E1, E2, M1, and M2 transitions from the ground state by taking into account the various checks for accuracy of wavefunctions. We have also estimated the lifetimes of all excited levels. Our results may be useful for plasma physicists for interpretation of spectra emitted by plasmas produced in fusion reactors.

Acknowledgment

M. M. is thankful to D. S. T. (INDIA), U. G. C. (INDIA) and the University of Delhi under R & D research programme for financial support.

Reference
1 Hawryluk R J, Campbell D J and Janeschitz Get al. 2009 Nucl. Fusion 49 065012 DOI:10.1088/0029-5515/49/6/065012 [Cited within:1] [JCR: 2.734]
2 Feng H, Wang C, Yang J, Jiang G and Hao L 2011 Phys. Scr. 84 015302 DOI:10.1088/0031-8949/84/01/015302 [Cited within:1]
3 Safronova U I and Safronova A S 2010 J. Phys. B 43 074026 DOI:10.1088/0953-4075/43/7/074026 [Cited within:6] [JCR: 3.607]
4 Huang K N 1986 At. Data Nucl. Data Tables 34 1 DOI:10.1016/0092-640X(86)90008-2 [Cited within:1]
5 Safronova U I, Sataka M, Albritton J R, Johnson W R and Safronova M S 2003 At. Data Nucl. Data Tables 84 1 DOI:10.1016/S0092-640X(03)00013-5 [Cited within:2]
6 Lavin C, Alvarez A B and Martin I 1997 J. Quant. Spectrosc. Radiat. Transfer 57 831 DOI:10.1016/S0022-4073(97)00006-X [Cited within:3]
7 Ralchenko Y, Draganic I N, Tan J N, Gillaspy J D, Pameroy J M, Reader J, Feldman U and Holland G E 2008 J. Phys. B: At. Mol. Opt. Phys. 41 021003 DOI:10.1088/0953-4075/41/2/021003 [Cited within:4] [JCR: 2.031]
8 Grant I P, Mckenzie B J, Norrington P H, Mayers D F and Pyper N C 1980 Comput. Phys. Commun. 21 207 DOI:10.1016/0010-4655(80)90041-7 [Cited within:2] [JCR: 3.078]
9 Norrington P H 2009http://www.am.qub.ac.uk/DARC/ [Cited within:2]
10 Quinet P 2012 J. Phys. B 45 025003 DOI:10.1088/0953-4075/45/2/025003 [Cited within:3] [JCR: 3.607]
11 Aggarwal S, Singh J and Mohan M 2013 Chin. Phys. B 22 033201 DOI:10.1088/1674-1056/22/3/033201 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
12 Singh A K, Aggarwal S and Mohan M 2013 Phys. Scr. 88 035301 DOI:10.1088/0031-8949/88/03/035301 [Cited within:1]
13 Aggarwal S, Singh J and Mohan M 2013 At. Data Nucl. Data Tables 99 704 DOI:10.1016/j.adt.2013.02.001 [Cited within:1]
14 Aggarwal S, Jha A K S and Mohan M 2013 Can. J. Phys. 91 394 DOI:10.1139/cjp-2013-0013 [Cited within:1] [JCR: 0.902]
15 Mohan M, Aggarwal S and Singh N 2014 Can. J. Phys. 92 177 DOI:10.1139/cjp-2013-0348 [Cited within:1] [JCR: 0.902]
16 Mohan M, Aggarwal S, Singh N and Jha A K S 2014 Can. J. Phys. 92 551 [Cited within:1] [JCR: 0.902]
17 Aggarwal S, Singh J, Jha A K S and Mohan M 2014 At. Data Nucl. Data Tables 100 859 DOI:10.1016/j.adt.2013.11.005 [Cited within:1]
18 Aggarwal S, Singh A K and Mohan M 2014 JAMCNP 1 19 [Cited within:2]
19 Kramida A 2011 Can. J. Phys. 89 551 [Cited within:1] [JCR: 0.902]
20 Kramida A E and Shirai T 2009 At. Data Nucl. Data Tables 95 305 DOI:10.1016/j.adt.2008.12.002 [Cited within:1]
21 Clementson J and Beiersdorfer P 2010 Phys. Rev. A 81 052509 DOI:10.1103/PhysRevA.81.052509 [Cited within:1] [JCR: 3.042]
22 Clementson J, Beiersdorfer P, Brown G V, Gu M F, Lundberg H, Podpaly Y and Trabert E 2011 Can. J. Phys. 89 571 DOI:10.1139/p11-028 [Cited within:1] [JCR: 0.902]
23 Pütterich T, Neu R, Dux R, Whiteford A D and Mullane M G Othe ASDEX Upgrade Team 2008 Plasma Phys. Control Fusion 50 085016 DOI:10.1088/0741-3335/50/8/085016 [Cited within:2] [JCR: 2.369]
24 Lennartsson T, Clementson J and Beiersdorfer P 2013 Phys. Rev. A 87 062505 DOI:10.1103/PhysRevA.87.062505 [Cited within:1] [JCR: 3.042]
25 Charro E, Lopez-Ferrero S and Martin I 2003 Astron. Astrophys. 406 741 DOI:10.1051/0004-6361:20030660 [Cited within:1] [JCR: 5.084]