†Corresponding author. E-mail: zyan@unb.ca
‡Corresponding author. E-mail: tyshi@wipm.ac.cn
*
In this paper, we overview recent advances in high-precision structure calculations of the hydrogen molecular ions (
Fundamental physical constants appear in mathematical formulas describing fundamental interactions in physical theories. Comparison of the same fundamental physical constant measured in different areas of physics can test the universality of the constant as well as the self-consistency of physical laws. The precision of a fundamental physical constant determines the accuracy of a theoretical prediction. Moreover, a space– time variation of a fundamental physical constant can reveal the domain of validity of a theory and provides further evidence for constructing a more general theory beyond the “ standard model of particle physics” .
The proton-to-electron mass ratio mp/me is one of the fundamental physical constants, which is relevant to the quantum chromodynamic scale.[1] Its high precision value is of great importance for testing the standard model of particle physics, and for exploring new physics beyond the standard model.[2– 5] Currently, the Committee on Data for Science and Technology (CODATA) recommended value for mp/me is 1836.15267245 with the relative standard uncertainty of 4.1 × 10− 10.[6] This value is determined indirectly by measuring the masses of the proton and the electron separately. Since the relative uncertainties of mp and me in the unified atomic mass unit (u) are 8.9 × 10− 11 and 4.0 × 10− 10[6] respectively, the uncertainty in mp/me is mainly due to the uncertainty of the electron mass. In fact, direct experimental measurement of me is challenging. One way to extract the electron mass is to compare the experimentally measured g factor of the electron in a hydrogenlike ion with the corresponding theoretical calculation based on quantum electrodynamic (QED) theory. This approach has been the most accurate method in the last decade.[7] Recently, Max Planck Institute for Nuclear Physics[8] in Germany has made a breakthrough on measuring the g factor of the electron in the hydrogenlike 12C5+ and has determined the electron mass with the relative precision of 3 × 10− 11, a factor of 13 improvement over the CODATA recommended value.
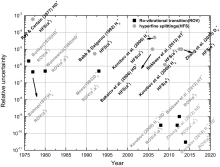
In addition to indirect measurements, the proton-to-electron mass ratio can also be measured directly. Figure 1 shows the precision of mp/me measured directly over the past 40 years. In earlier times, mp/me was determined by measuring the cyclotron frequencies of a free proton and a free electron in the same magnetic field, [9– 16] where the energy scales involved were in the high energy range of GeV to TeV. In the last decade, due to rapid development of new techniques, such as femtosecond optical comb and laser cooling and trapping, atomic and molecular spectroscopy can be measured to an unprecedented high precision at the level of Hz or sub-Hz, which has created many opportunities to test physical laws in low energy eV region.[17, 18] With an increase of precision, small shifts in atomic and molecular energy levels can reveal small but subtle physical effects, such as high-order relativistic and QED (radiative) corrections, contributions from unknown particles beyond the standard model of particle physics, and effects due to symmetry breakings.[19, 20] A comparison between spectroscopic measurements and theoretical calculations can be used to determine fundamental physical constants involved, such as the proton-to-electron mass ratio mp/me (or mp̄ /me)[21– 23] (see the last three measurements in Fig. 1). Direct and indirect measurements of mp/me can not only provide diversified methods but also check self-consistency among the proton mass mp, the electron mass me, and the ratio mp/me. The self-consistency can ensure that these three constants are fundamental; furthermore a precise mass ratio mp/me can impose a strict constraint on the individual values of mp and me. A violation of this self-consistency may indicate the existence of new physics.
 | Fig. 1. Relative uncertainty of mp/me measured directly. These measurements were carried out at Johannes Gutenberg-Universitä t Mainz (JGU), [9, 10] University of Washington (UWash), [11– 13] National Institute of Standards and Technology (NIST), [14] Harvard University (Harvard), [16] the European Organization for Nuclear Research (CERN), [21, 22] and Heinrich-Heine-Universitä t Dü sseldorf (UDuss).[23] |
So far, several experiments have been performed to measure mp/me (or mp̄ /me) directly by studying spectroscopic data. These high precision measurements focus on the antiprotonic helium and the hydrogen molecular ions which can be used to directly determinate mp̄ /me and mp/me, respectively. Moreover, a comparison between mp̄ /me and mp/me can test the CPT (charge, parity, and time reversal) symmetry variation.
Since its establishment, the atomic spectroscopy and collisions using slow antiprotons (ASACUSA) collaboration has been working on precision spectroscopies of atoms containing the antiproton, [20] such as the antihydrogen atom 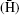
Compared to p̄ He+ , rovibrational states of hydrogen molecular ions (
This article is organized as follows. The background of high-precision spectroscopy is introduced in Section 1.2 for hydrogen molecular ions, which includes theory and experiment. In Section 2, theoretical formulation for solving a three-body bound-state problem is presented, including the nonrelativistic energy eigenvalue problem and the leading- and higher-order relativistic and QED corrections. In Section 3, an experimental scheme is described for measuring the rovibrational transition frequency v : 0 → 6 in HD+ , which is currently underway at the Wuhan Institute of Physics and Mathematics. In Section 4, a summary is given.
The hydrogen molecular ion, the simplest molecule in nature, can be considered as a three-body quantum mechanical system consisting of one electron and two nuclei. Some of its rovibrational states have lifetimes longer than 10 μ s, and the probability of making a dipole transition can be strong enough to allow for a precision measurement of its spectroscopy.[2, 27, 33– 35] On the other hand, the transition frequency between two specific rovibrational states can be calculated to sufficiently high precision using the three-body QED theory.[30, 31] Since the theoretical frequency of a rovibrational transition in the hydrogen molecular ion contains effects due to the proton-to-electron mass ratio, a comparison between theory and experiment of its spectroscopy holds a potential of extracting a precise value of mp/me.[2, 3]
Theoretically, a transition frequency in the hydrogen molecular ion can be expanded in powers of the fine structure constant α (≈ 1/137) according to the theory of nonrelativistic QED (NRQED).[36, 37] The structure of an energy level contains the contributions from the nonrelativistic term, the leading-order relativistic and QED corrections of order R∞ α 2 and R∞ α 3 respectively, where R∞ is the Rydberg constant, and the correction due to the finite nuclear size. Higher-order relativistic and QED corrections can be added in when they become necessary.
In order to determine a transition frequency, the nonrelativistic energy eigenfunction and the eigenvalue can be obtained by solving the three-body Schrö dinger equation variationally. In previous work, the rovibrational states of the hydrogen molecular ions were calculated at different levels of approximation, such as the Born– Oppenheimer approximation, the adiabatic approximation, and the non-adiabatic approximation.[38– 40] In 1985, Bishop and Solunac[41, 42] broke down the Born– Oppenheimer and adiabatic approximation and calculated the energy levels of the hydrogen molecular ions precisely. From then on, the energy levels of 


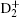

 | Fig. 2. Theoretical hyperfine splittings and rovibrational transition frequencies for the hydrogen molecular ions. |
In 2006, Korobov[30] not only evaluated the R∞ α 2 and R∞ α 3 order corrections to high precision but also considered for the first time the higher-order terms of R∞ α 4 and R∞ α 5, beyond the adiabatic approximation. The largest part of the uncertainty in his calculation was due to the theoretical approximation of the R∞ α 5 term. The uncertainty in the transition frequency (v, L) : (0, 0) → (1, 0) for 




Spectroscopic measurements of rovibrational and hyperfine structures of hydrogen molecular ions have been carried out since 1960s. Figure 3 shows a time evolution of some important measurements. During the early stages, the measured spectra were much less precise than their neutral counterparts. High-order relativistic and QED effects of spin– spin and spin– orbital interactions have never been tested on these ions until recently. With developments of new experimental techniques, such as laser cooling and trapping, and sympathetic cooling, [85] together with the emergence of new laser systems, [86] precision measurements of cold molecules and molecular ions have received considerable attention. Cold and trapped ions have a range of advantages for spectroscopic applications. First, experiment on single trapped ions can avoid inhomogeneous spectral line broadening resulting from ensemble averaging. Second, the low translational velocities of the ions can minimize Doppler broadening. Third, a long storage time allows a measurement to go over an extended period of time. Finally, an ultra-high vacuum apparatus provides a well-defined experimental environment where interactions with surroundings are minimized or well controlled. All these can make enhancement of spectroscopic resolution possible.
Schiller’ s group at Dü sseldorf[23, 33] pioneered an experimental measurement of a rovibrational transition in sympathetically cooled HD+ ions. In their experiments, the HD+ ions were sympathetically cooled into a Be+ Coulomb crystal. High-resolution infrared spectroscopy on the HD+ ions was recorded for the rovibrational transition of (v, L) : (0, 2) → (4, 3) at a wavelength around 1.4 μ m. Though the spectral resolution of about 40 MHz was limited by the residual Doppler broadening, the spectral line position was determined with a relative accuracy of 2 ppb. Combining with the Korobov’ s theoretical prediction, the proton-to-electron mass ratio mp/me was determined at the level of 5 ppb. In 2012, the same group made further progress on the measurement of the rovibrational transition (v, L) : (0, 0) → (1, 1) with the accuracy of 1.1 ppb.[26] The improvement of the experimental accuracy was achieved by using the optical pumping method to increase the rovibrational ground state population. The population transfer efficiency was achieved at 60%– 70% in their experiments.[87] There are other two groups currently working on the precision spectroscopy of the hydrogen molecular ions HD+ and 


According to the theory of NRQED, [36, 37] the total energy of a state in 
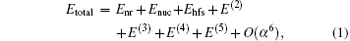
where Enr is the nonrelativistic energy, Enuc is the correction due to the finite nuclear size, Ehfs is the correction from the hyperfine structure, and E(n) is the correction of order R∞ α n. The effect of hyperfine structure in an experimental measurement can be removed according to theoretical calculation of hyperfine splittings, and the transitional frequency is then obtained. Ehfs has been well calculated in series of works for HD+ [69] and 
We begin with the nonrelativistic Hamiltonian of a three-body Coulombic system,
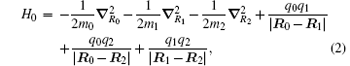
where mi, qi, and Ri are the mass, charge, and position vector of the ith particle, respectively. The total angular momentum operator, which commutes with H0, is

For the purpose of isolating the center-of-mass motion, we make the following coordinate transformations:

where 
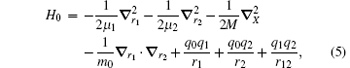
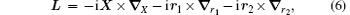
where r12 = | r1 − r2| and μ i = mim0/(mi + m0). Since X is cyclic, we can simply neglect X. Therefore in the center-of-mass frame,
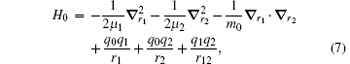
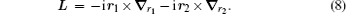
This Hamiltonian can be thought of as the one describing two “ effective particles” moving relative to particle 0 sitting at the origin. It is noted that one has freedom to choose any particle as particle 0. For the hydrogen molecular ions 
The Schrö dinger equation for the system is therefore expressed as H0ψ 0 = E0ψ 0, where E0 is the energy eigenvalue and ψ 0 is the corresponding eigenfunction. For solving the eigenvalue problem for H0 variationally, we seek the common eigenstates of the commuting observables {H0, L2, Lz, Π }, where Π is the parity operator, using the following basis set in Hylleraas coordinates:

In the above, 
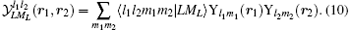
The vibrational degrees of freedom between two the nuclei should be sufficiently represented in the basis set, according to the picture of the Born– Oppenheimer approximation, as pointed out by Bhatia and Drachman.[89] They suggested to use Gaussian-like function ρ N e− bρ to simulate the vibrational modes, where ρ is the distance between the two nuclei, and N and b are two big numbers satisfying b ≈ N/2. Since we choose one nucleus as particle 0 and the other as particle 2, the vibrational part in our basis can be described by 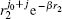

If the two nuclei are identical, such as 
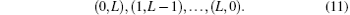
Each configuration (l1, l2) has its own nonlinear parameters α and β . Since the nuclei carry most of the angular momentum, the leading configuration (0, L) is divided into NL sub-blocks, each having its own nonlinear parameters α and β , according to the following scheme:[53] the nth block in the configuration (0, L) contains all the terms satisfying the following relations for the power jn of r2:
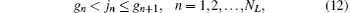
where

int[x] stands for the integer part of x, and Ω is an integer controlling the size of each block. The basis set is generated by including all terms such that

The basis set constructed this way can sufficiently represent the vibrational modes in the wavefunction. Moreover, if we include some terms with lower powers of r2, the rate of convergence, along with the numerical stability in the wavefunction, can be further enhanced.[56] Hence another small-size block with j0 = l2 is added to our basis set. A complete optimization is performed with respect to those nonlinear parameters by minimizing the energy eigenvalue. This involves the calculation of the energy derivative ∂ E/∂ α with respect to each nonlinear parameters.[55]
The basic type of integrals that appear in our variational calculation are of the form
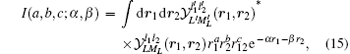
which can be evaluated analytically in terms of the hypergeometric function 2F1(a, b; c; x).[90] The procedure for handling singular integrals appearing in the evaluation of the Breit operators can be found in Ref. [91] where the singular parts are exactly canceled out with each other. Another method to deal with singular integrals was developed by Harris and coworkers[92] where the singular parts are simply dropped out. It should be pointed out that these two methods are equivalent.
Table 1. Nonrelativistic energies for various rovibrational states in  |
The nonrelativistic energies of the hydrogen molecular ions 

The leading-order relativistic corrections due to the Breit operators are R∞ α 2. For a general atomic or molecular system, these corrections can be obtained by reducing the relativistic four-component wavefunction of the Dirac equation to a two-component one in its nonrelativistic form.[93– 96] The major part of the R∞ α 2 corrections is due to the relativistic bound electron which, for the hydrogen molecular ion, has the form of

There also exist the so-called recoil corrections of R∞ α 2(me/mnuc) and R∞ α 2(me/mnuc)2, which are caused by the finite nuclear masses. The first of this type is the retardation terms coming from the exchange of transverse photon
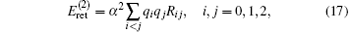
where
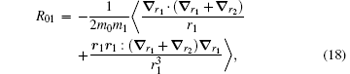
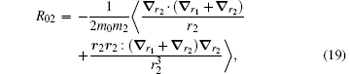
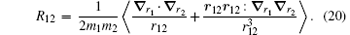
The correction 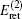
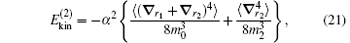
which is rooted from the dependence of the relativistic mass on velocity: 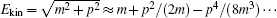
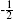


and the Darwin term for HD+ is
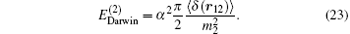
The complete contribution of the leading-order relativistic correction is thus

For the case of 

The numerical values for the above discussed operators are presented in Table 2 for 
Table 2. Numerical values of the Breit operators 〈 δ (r1)〉 , 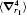 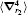  |
Table 3. Numerical values of the Breit operators 〈 δ (r12)〉 , 〈 δ (r1)〉 , 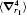 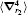 |
| Table 4. Numerical values of the Breit operators R02, R01, and R12 for HD+ , where v = 0− 4 and L = 0− 4. |
The leading-order radiative corrections of R∞ α 3 is the largest part of the QED shift. For an atomic or molecular bound state, the current theoretical formalism for evaluating the QED corrections is based on the NRQED theory.[36, 98– 100] The one-loop self-energy correction is
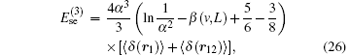
where β (v, L) is the Bethe logarithm. The correction of the anomalous magnetic moment of order R∞ α 3 is

which may be integrated into Eq. (26) as a contribution from the form factor of the electron.[101] The Coulomb interaction between the bound electron and an external field can be represented by exchanging Coulomb photons. According to QED, a Coulomb photon generates virtual electron– positron pairs which are then annihilated into photons. As a result, the energy of the Coulomb photon has a shift. The correction of one-loop vacuum polarization, which has one electron– positron pair, is
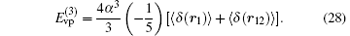
The interaction that the bound electron exchanges a Coulomb photon and a transverse photon with nucleus contributes to the energy shift. Thus, the order R∞ α 3(me/mnuc) correction of one transverse photon exchange is
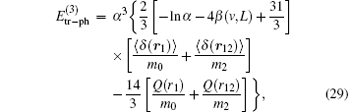
where Q(r) is the Q term introduced by Araki[102] and Sucher.[103] Summarizing all the contributions of order R∞ α 3, one obtains

In the basis set of Eq. (9), the Q terms can be expressed as[104]

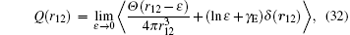
where γ E is Euler’ s constant, ε is the radius of a sphere about r = 0 to be excluded from the integration for Q(r). Numerical values of these terms can be found in Table 5 and Table 6 for 
Table 5. Numerical values of Q(r1) for  |
| Table 6. Numerical values of Q(r1) and Q(r12) for HD+ , where v = 0− 4 and L = 0− 4. For each (v, L), the first entry is for Q(r1) and the second is for Q(r12). |
The Bethe logarithm β (v, L), the most difficult to calculate, is responsible for the nonrelativistic part of the self-energy of a charged particle in a quantum state interacting with transverse photons. The Bethe logarithm can either be represented by a sum over intermediate states[95, 105] or by an integral over intermediate photon momentum k, [106] according respectively to


where | ψ 0〉 is the energy eigenstate of interest with the corresponding energy eigenvalue E0; J = ∑ aqaPa/ma is the electric current density operator of the system with qa, Pa, and ma being respectively the charge, the momentum operator relative to a laboratory coordinate system, and the mass of particle a; the summation over i covers all virtual intermediate states connected to | ψ 0〉 by the operator J; and (H0 − E0 + k)− 1 is the resolvent operator associated with the nonrelativistic Hamiltonian H0. Korobov[107] applied the approach of Schwartz[106] to evaluate β (v, L) for the hydrogen molecular ions according to Eq. (34) and obtained about 5– 6 significant digits for HD+ [108] and 



Table 7. Bethe logarithms for low-lying rovibrational states of  |
| Table 8. Bethe logarithms for low-lying rovibrational states of HD+ , see Table 5 of Ref. [81]. |
The corrections of order R∞ α 4 are also needed to be taken into consideration.[31, 114, 115] However, the recoil corrections of order R∞ α 4(me/mnuc) and higher are small and can be neglected at the precision of ∼ 0.01– 0.1 ppb. The self-energy and the vacuum polarization corrections at this order are respectively
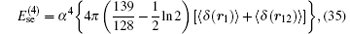
and
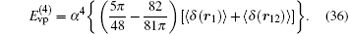
Note that in Ref. [31], the above term 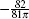

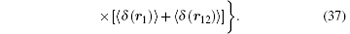
Finaly the contribution due to the second-order slope of the Dirac form factor is
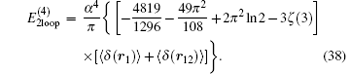
Summing up all the contributions, the total radiative correction of order R∞ α 4 in the external field approximation can be expressed as
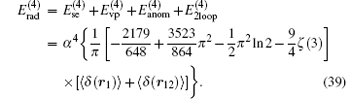
Currently, the order R∞ α 4 relativistic corrections are calculated in the two-center approximation.[31, 116] In this approximation, the Hamiltonian of the nonrelativistic Schrö dinger equation is expressed as
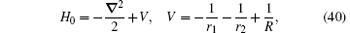
where R is the distance between the two nuclei, and r1 and r2 are the distances from the electron to nuclei 1 and 2, respectively. The total relativistic correction to the energy of a bound electron at order R∞ α 4 is calculated according to
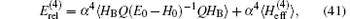
where Q = 1 − | ψ 0〉 〈 ψ 0| is the projection operator and HB is the Breit– Pauli Hamiltonian defined by

The effective Hamiltonian 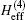
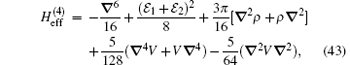
where 
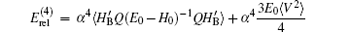

which can be evaluated numerically. The numerical values of 

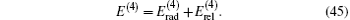
Table 9. Relativistic corrections of order R∞ α 4 for  |
| Table 10. Relativistic corrections of order R∞ α 4 for HD+ . Units are α 4 a.u. |
The next order of corrections that we should consider is R∞ α 5, which contain the contributions of the self-energy, the vacuum polarization, the Wichman– Kroll term, the complete two-loop diagrams, and the three-loop diagrams. The R∞ α 5 order corrections for hydrogenlike ions can be found in Refs. [114], [115], and [117]. In early times, these corrections were calculated in the hydrogen approximation where the parameters of hydrogen were adopted.[30, 31] In 2014, the R∞ α 5 order corrections were extended by Korobov et al.[83, 84] to a system of two Coulomb centers. Thus the two-center approximation used for the R∞ α 4 order relativistic corrections will also be used in the following equations.
The main part of this shift is the self-energy contribution. The general results obtained in Refs. [118]– [120] for a bound electron in an external field were taken as the starting point in the work of Korobov et al. Since in Refs. [118]– [120] the form of field is generic, it is possible to extend their approach to the two-center problem. The details of the derivation can be found in Ref. [84]. The final result is

where A62 = − 1, and the expressions of A60 and A61 are

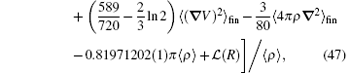
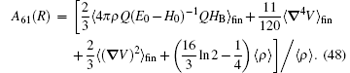
In the above, 〈 〉 fin means that the matrix elements are redefined in finite forms, and the other notations can be found in Section 2.4. The most difficult part to calculate is the relativistic Bethe logarithm 𝓛 (R), which has been evaluated by Korobov and coworkers[82] for the two-center problem. For the vacuum polarization in a strong external field, the leading-order correction is the Uehling term,

which contributes at the level of 1 kHz and can thus be estimated in the hydrogen approximation. The coefficients for an S state of the atomic hydrogen are
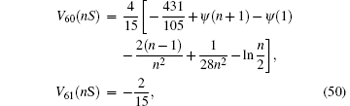
where V60(nS) is taken from Refs.[121]– [124] and V61(nS) from Ref. [125]. The Wichman– Kroll term[126] can be expressed in the form

The next contribution is the complete two-loop Feynman diagrams[127– 129]

where B50 = − 21.55447(12). This expression is valid for a bound electron in an arbitrary configuration of a few pointlike Coulomb sources. The contribution from the three-loop Feynman diagrams at this order is[130– 133]
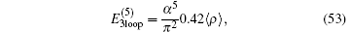
which may be negligible. The total contribution of order R∞ α 5 is therefore

In addition to these corrections discussed above, the dominant part of R∞ α 6 is also considered, which represents the second-order perturbation with two one-loop self-energy operators
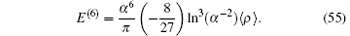
The electron in the hydrogen molecular ion is settled in the 1σ g state with its principal quantum number n = 1 and the angular momentum quantum number l = 0. In the hydrogen approximation, it can be simplified as a 1s state. Thus, we can calculate the corrections of the finite nuclei size using the formula for the s-state hydrogen or deuterium. According to Refs. [114] and [115], the leading-order correction of the finite nuclear size is given by
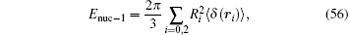
where R0 and R2 are the root-mean-square radii of the two nuclear charge distributions. It is Rp = 0.8775(51) fm for the proton and Rd = 2.1424(21) fm for the deuteron.[6] The next-order correction is given by (see Ref. [6] and references therein)
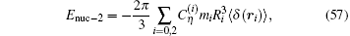
where 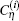
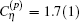
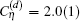
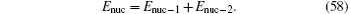
The total transition frequency is obtained by summing up all the contributions

where Ei and Ef are the energy levels of the initial and final states, respectively. Table 11 lists individual contributions up to R∞ α 6 to the fundamental transition (v, L) : (0, 0) → (1, 0) in 


Table 11. Summary of contributions to the transition frequency (v, L) : (0, 0) → (1, 0) of  |
Table 12 lists some important transition frequencies in HD+ , together with the available experimental measurements. For the transition (v, L) : (0, 0) → (1, 1), there is a discrepancy of about 150 kHz between theory and experiment. At first glance, this seems to be introduced by the higher-order correction of the finite nuclear size effect that is ignored in previous works. However, this correction to (v, L) : (0, 0) → (1, 1) is estimated to be only + 34 kHz, indicating that the resulting discrepancy is now increased to 180 kHz. The reason for this discrepancy is unknown.
The motion-induced Doppler broadening is the main factor affecting the precision and resolution of rovibrational spectroscopy in the hydrogen molecular ions. Reducing the translational energy of the ions and confining them in the Lamb– Dicke region can minimize the first-order Doppler shift and broadening to the greatest extent.[25]
The complexity of the molecular energy level structure usually prevents the implementation of closed optical cycles so that laser cooling is generally not applicable to molecules or molecular ions. Over the past 15 years, sympathetic cooling[136, 137] has emerged as a versatile method for cooling a broad range of molecular ions to millikelvin secular temperatures with laser-cooled atomic ions.[138– 140] Since the molecular ions can exchange kinetic energy with the laser-cooled atomic species by Coulomb interactions, it is possible to reduce the molecular ions’ kinetic energy. Thus, the atomic-ion species act as a coolant for the molecular ions resulting in the formation of bi-component (or molecular) Coulomb crystals.
The hydrogen molecular ions can be sympathetically cooled either using laser-cooled beryllium ions Be+ or magnesium ions Mg+ . Due to the lower mass ratio between Be+ and HD+ , using Be+ as a coolant can provide higher cooling efficiency and lower secular temperature than using Mg+ . However, making a radiation source for laser cooled Be+ is technologically demanding; on the other hand, using laser cooled Mg+ as a coolant for sympathetically cooling HD+ has advantages in terms of experimental complexity and cost.
Early theoretical work[141] gives the critical mass ratio for using heavy ions to sympathetically cool light ions, but this theoretical threshold has been overcome experimentally.[142] The more reliable method to determine the feasibility of performing high-efficiency sympathetic cooling between different ions is the use of molecular dynamics (MD) to simulate such a cooling process. An MD simulation can also provide the characteristic information of molecular Coulomb crystal, e.g., the number of the laser-cooled and sympathetically cooled ions and their translational energies. We simulated 150 laser-cooled Mg+ ions to sympathetically cool ten HD+ ions and obtained an image of bi-component Coulomb crystal (see Fig. 4). The result shows that HD+ can be sympathetically cooled into the Mg+ Coulomb crystal and form a chain of almost stationary (T ≤ 10 mK) molecular ions. At this temperature, the resolution of rovibrational spectroscopy of HD+ can be obtained in about 10 MHz range. As we know, the spectral linewidth resulting from the Doppler broadening is proportional to 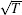
Translationally cold molecular ions are conventionally produced from “ warm” samples by sympathetic cooling. Because low-energy collisions between ions are dominated by the Coulomb interaction which does not couple to the internal degrees of freedom, sympathetically cooled ions exhibit a broad distribution of the rotational-state population.[143, 144] In such translationally cold but internally warm samples, the population can be accumulated in the rotational ground state using optical pumping scheme as demonstrated by Drewsen et al.[139] and Schneider et al.[87] Although optical pumping can increase the population of the rovibrational ground state by an order of magnitude higher than the corresponding thermal population at room temperature, the state preparation is not complete. A novel method has been developed to prepare internally state-selected molecular ions in a linear Paul ion trap.[143, 144] The technique relies on the generation of molecular ions in a well-defined rovibrational quantum state using photoionization followed by sympathetic cooling of the translational motion with laser-cooled atomic ions.
Such a technique can be applied to prepare a single rovibrational quantum state in HD+ by resonance-enhanced threshold photoionization (RETPI) method.[145] The experimental process includes the following three steps, as depicted in Fig. 5. First, neutral HD molecules are accumulated at low rovibrational states in a molecular beam due to the adiabatic expansion; second, an excitation laser of λ 1 ≈ 327 nm is applied to populate HD to an exited electronic state. Finally, by setting a photoionization photon energy of λ 2 ≈ 314 nm slightly above the desired ionic state accessible by the selection rules, HD+ ions can be generated in a single rovibrational level.
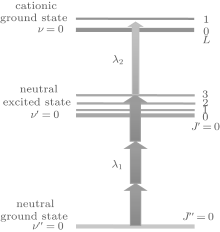 | Fig. 5. State selective [3+ 1′ ] resonance-enhanced threshold-photoionization scheme used to generate HD+ ions in the rovibrational ground state. |
Since the RETPI method can produce molecular ions selectively due to the propensity rule of the excitation and ionization, it avoids generating undesired high abundant molecular species, such as 
High-resolution infrared spectroscopy on sympathetically cooled HD+ ions can be performed by using resonance-enhanced multiphoton dissociation (REMPD) spectroscopy.[23, 146] The rovibrational transition (v, L) : (0, 0) → (6, 1) can be measured by using a single photon excitation at 991 nm. The absorption of an additional 355 nm photon from the vibrationally excited state results in photofragmentation of the ions. By comparing with an MD simulation, the rate of fragmentation can be derived from the time-resolved image change of the bi-component Coulomb crystal.
The probability of vibrational overtone transitions is much lower than the fundamental transitions. For example, the probabilities of transitions from v : 0 → 4 and v : 0 → 8 are 4 and 7 orders of magnitude lower than the fundamental transition of v : 0 → 1 respectively. However, the sympathetically cooled molecular ions are spatially stationary (T ∼ mK, trapping time ∼ hours), which can provide a minute-long interaction time between photons and ions. This unprecedentedly long interaction time ensures successful excitation of the vibrational overtone transitions.
In 2007, Schiller’ s group observed the overtone transitions of v : 0 → 4 in HD+ at the rate of 22 s− 1 using a laser with 170 μ W in power and 200 μ m of beam waist.[23] The Einstein coefficient B of the v : 0 → 6 transition is proximately 1/400 of the transition v : 0 → 4. We estimate the rate of transition by employing a laser of 100 kHz linewidth, 100 mW in power, and 200 μ m beam waist to be achieved at 64 s− 1, which is faster than the other observed overtone transitions of v : 0 → 8.[27] The hyperfine transition linewidth in sympathetically cooled HD+ ions is around 10 MHz, which is dominated by the Doppler broadening of the residual thermal energy. The radiation intensity of the above proposed laser system would not bring an additional broadening of the measured transition linewidth. The uncertainty of the induced AC Stark shift is on the order of 10− 12, which will evidently not affect the targeted accuracy.
The past few years have witnessed impressive progress in the field of sympathetic cooling of molecular ions. New experimental methods have been developed, which allow for an effective control of molecular internal quantum sates. Such developments have opened up a variety of opportunities for spectroscopic measurements of molecular ions with high precision. In our project/proposal, the hydrogen molecular ions HD+ can be generated to the rovibrational ground state by RETPI, and can be sympathetically cooled to millikelvin by laser-cooled atomic ions. With this accurate control of internal and external degrees of freedom, the overtone transition frequency from the rovibrational ground state to the 6th rovibrational excited state can be determined by the REMPD method. The relative accuracy of the measured transition frequency around 991 nm is expected to reach 0.4 ppb.
On the theoretical side, the contributions up to R∞ α 5 have been taken into account in the calculations of the transition frequencies of 

We would like to thank Shu-Min Zhao, Li-Yan Tang, Pei-Pei Zhang, and Quan-Long Tian for their participation and contributions. We also thank Kelin Gao and Hua Guan for valuable discussion, and V. I. Korobov of JINR for his expertise and encouragement.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|
| 55 |
|
| 56 |
|
| 57 |
|
| 58 |
|
| 59 |
|
| 60 |
|
| 61 |
|
| 62 |
|
| 63 |
|
| 64 |
|
| 65 |
|
| 66 |
|
| 67 |
|
| 68 |
|
| 69 |
|
| 70 |
|
| 71 |
|
| 72 |
|
| 73 |
|
| 74 |
|
| 75 |
|
| 76 |
|
| 77 |
|
| 78 |
|
| 79 |
|
| 80 |
|
| 81 |
|
| 82 |
|
| 83 |
|
| 84 |
|
| 85 |
|
| 86 |
|
| 87 |
|
| 88 |
|
| 89 |
|
| 90 |
|
| 91 |
|
| 92 |
|
| 93 |
|
| 94 |
|
| 95 |
|
| 96 |
|
| 97 |
|
| 98 |
|
| 99 |
|
| 100 |
|
| 101 |
|
| 102 |
|
| 103 |
|
| 104 |
|
| 105 |
|
| 106 |
|
| 107 |
|
| 108 |
|
| 109 |
|
| 110 |
|
| 111 |
|
| 112 |
|
| 113 |
|
| 114 |
|
| 115 |
|
| 116 |
|
| 117 |
|
| 118 |
|
| 119 |
|
| 120 |
|
| 121 |
|
| 122 |
|
| 123 |
|
| 124 |
|
| 125 |
|
| 126 |
|
| 127 |
|
| 128 |
|
| 129 |
|
| 130 |
|
| 131 |
|
| 132 |
|
| 133 |
|
| 134 |
|
| 135 |
|
| 136 |
|
| 137 |
|
| 138 |
|
| 139 |
|
| 140 |
|
| 141 |
|
| 142 |
|
| 143 |
|
| 144 |
|
| 145 |
|
| 146 |
|
| 147 |
|




