Cite this Article
Gu Hua-Guang, Chen Sheng-Gen, Li Yu-Ye. Complex transitions between spike, burst or chaos synchronization states in coupled neurons with coexisting bursting patterns* . Chinese Physics B, 2015, 24(5): 050505  
Permissions
Complex transitions between spike, burst or chaos synchronization states in coupled neurons with coexisting bursting patterns*
Gu Hua-Guanga)†, Chen Sheng-Gena), Li Yu-Yeb)
School of Aerospace Engineering and Applied Mechanic, Tongji University, Shanghai 200092, China
Mathematics & Statistics Institute, Chifeng University, Chifeng 024000, China

†Corresponding author. E-mail: guhuaguang@tongji.edu.cn

*Project supported by the National Natural Science Foundation of China (Grant Nos. 11372224 and 11402039) and the Fundamental Research Funds for Central Universities designated to Tongji University (Grant No. 1330219127).

Abstract

We investigated the synchronization dynamics of a coupled neuronal system composed of two identical Chay model neurons. The Chay model showed coexisting period-1 and period-2 bursting patterns as a parameter and initial values are varied. We simulated multiple periodic and chaotic bursting patterns with non-(NS), burst phase (BS), spike phase (SS), complete (CS), and lag synchronization states. When the coexisting behavior is near period-2 bursting, the transitions of synchronization states of the coupled system follows very complex transitions that begins with transitions between BS and SS, moves to transitions between CS and SS, and to CS. Most initial values lead to the CS state of period-2 bursting while only a few lead to the CS state of period-1 bursting. When the coexisting behavior is near period-1 bursting, the transitions begin with NS, move to transitions between SS and BS, to transitions between SS and CS, and then to CS. Most initial values lead to the CS state of period-1 bursting but a few lead to the CS state of period-2 bursting. The BS was identified as chaos synchronization. The patterns for NS and transitions between BS and SS are insensitive to initial values. The patterns for transitions between CS and SS and the CS state are sensitive to them. The number of spikes per burst of non-CS bursting increases with increasing coupling strength. These results not only reveal the initial value- and parameter-dependent synchronization transitions of coupled systems with coexisting behaviors, but also facilitate interpretation of various bursting patterns and synchronization transitions generated in the nervous system with weak coupling strength.

Keyword: 05.45.Xt; 87.18.Tt; 87.18.Hf; synchronization transition; phase synchronization; coexisting attractors; coupled neuronal system
1. Introduction

Synchronization is widespread in nature.[1, 2] Chaos synchronization has been one of the most important issues.[1, 3] In particular, synchronization was experimentally detected in the nervous system of the mammalian visual cortex, the human thalamocortical area, and the stomatogastric ganglion of the spiny lobster.[4– 6] Transitions between various synchronization states were observed in the oddball task experiment and evidenced in the human cardiorespiratory system.[7– 9] It is believed that synchronization and synchronization transition are closely related to nervous information transmission and processing.[4, 8– 11] Physiologically, bursting is an important neural rhythm in the nervous system and is also important for information processing.[12– 16] Recently, there have been various simulations of synchronization and synchronization transition in the nervous system.[17– 22]

In most investigations of synchronization, the unit in the network or coupled system always manifests mono-stable behaviors. With the exception of mono-stable behavior, multi-stable and/or coexisting states are also common behaviors of a nonlinear system. The coexisting behavior of the dynamic system for a given set of parameters is determined by the initial values. Multi-stable behaviors occur in multiple fields, including biological science.[23] In the nervous system, the coexistence of resting condition and firing, [24– 26] of spiking and bursting, [27– 29] and of two different bursting patterns[30] were observed in experiments and simulated in theoretical models.

Recently, a few works have focused on the synchronization of unidirectionally coupled systems, [31– 38] which manifest, when isolated, multi-stable or coexisting behaviors. These studies are briefly described as follows. Two coupled Rö ssler-like electronic circuits with coexisting chaotic attractors were investigated experimentally and numerically.[31– 33] In that work the synchronization transitions moves from asynchronous motion to intermittent anticipating phase synchronization and generalized synchronization moves to a completely synchronized state as the coupling strength increases. The behaviors of asynchronous synchronization jump between the coexisting attractors. The synchronization dynamics of two coupled bistable Hé non maps were investigated.[34] When two periodic orbits coexist, the slave map evolves into the master map state. When chaotic and periodic attractors coexist, very complex dynamics, such as the emergence of new attractors are observed. Synchronization of coupled optical bistable systems with coexisting different attractors (fixed point and chaos, fixed point and one periodic orbit, and two periodic orbits) was investigated.[35]

Depending on both the control parameters of an isolated system and the coupling strength, different bifurcations and diverse dynamic regimes including periodicity and chaos occur in the route from asynchronous motion to complete synchronization. There also exists work on the nervous systems with bi-directional coupling.[36, 37] One previous study[36] investigates the synchronization transitions of two coupled neurons with coexisting spiking and bursting. Three different configurations of a coupled system, one neuron spiking and the other bursting, both types of spikings and both types of burstings, are considered. The complete synchronization at stronger coupling strength and synchronization transitions depends on the configurations. For the configuration of one spiking and the other bursting, the synchronization transitions for three parameter values within the coexisting parameter region was investigated.[37] The results showed that the complete synchronization and synchronization transition depend on the parameter values. In both investigations, only one initial value is considered, and the influences of different initial values on the complete synchronization and synchronization transitions have not been addressed.

In this paper, we comprehensively study the synchronization and synchronization transitions of two bi-directionally coupled Chay model neurons with coexisting burstings. We considered different configurations of the network, the initial values and the control parameters. We investigated different synchronization states, various bursting patterns corresponding to different synchronization states, and complex synchronization transitions, which range from non-synchronization to complete synchronization and is composed of different synchronization states. We identified the dependence of the complete synchronization on the initial values and control parameters. We also identified the synchronization transitions containing transitions between spike and burst phase synchronization (i.e., chaos synchronization), and transitions between spike and complete synchronization. The rest of this paper is organized as follows. Section  2 describes the Chay model and the coexisting burstings. Section  3 introduces the network model, initial values, and criteria for synchronization. The synchronization states and the corresponding rhythms are introduced in Section  4. Section  5 provides the detailed synchronization transitions and the influence of the parameter and initial values. Section 6 is the conclusion and discussion.

2. Chay model and dynamics of single neuron
2.1. Chay model

The Chay model was initially set up to describe the bursting patterns of β -cells[39] and manifested bifurcations similar to those observed in an experimental neural pacemaker.[40– 42] The Chay model is described using the following three differential equations:

Here, V, n, and C are the membrane potential, the probability of opening the voltage-sensitive K+ channel, and the intracellular concentration of Ca2+ , respectively. Vi, Vk, and Vl are the reversal potentials for mixed Na+ – Ca2+ , K+ , and leakage ions, respectively. gi, gkv, gkc, and gl represent the maximum conductance of the mixed Na+ – Ca2+ , voltage-dependent K+ , calcium-dependent potassium, and leakage ions, respectively. m∞ and h∞ are the probabilities of activation and inactivation of the mixed inward current channel, and n∞ is the steady state value of n. m∞ , h∞ , and n∞ could be expressed by y∞ = α y/(α y+ β y) in general, y stands for m, h, or n, and α m = 0.1(25+ V)/(1− e− 0.1V− 2.5), β m = 4e− (V+ 50)/18, α h = 0.07e− 0.05V− 2.5, β h = 1/(1+ e− 0.1V− 2), α n = 0.01(20+ V)/(1− e− 0.1V− 2), β n = 0.125e− (V+ 30)/80. The relaxation time of the voltage-gated K+ channel is τ n = 1/(λ n(α n+ β n)). KC is the rate constant for the efflux of the intracellular Ca2+ ions, and ρ is a proportionality constant. The parameter values of the Chay model are as follows: gi = 1800, gkv = 1700, gkc = 10, gl = 7, Vk = − 75, Vl = − 40, Vi = 100, Kc = 3.3/18, λ n = 227.5, ρ = 0.27. The unit of potential, conductance, and time is mV, pS, and sec, respectively. Detailed descriptions of the Chay model are given in a previous study.[39]

The parameter VC, the reversal potential of Ca2+ , here serves as the bifurcation parameter. The Chay model is solved using the fourth-order Runge– Kutta integration method with time step of 0.001  sec.

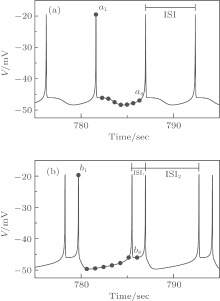
2.2. Coexistence of period-1 bursting and period-2 bursting

When VC = 308.1, the coexistence of period-1 bursting and period-2 bursting can be simulated with the Chay model. When the initial values of (V, n, C) are set to (− 47.733563, 0.105692, 0.511172) for period-1 bursting and (− 48.365978, 0.100857, 0.518610) for period-2 bursting, the Chay model exhibits period-1 bursting (Fig.  1(a)) and period-2 bursting (Fig.  1(b)), respectively. The inter-spike interval (ISI) of period-1 bursting is a constant value, and the period-2 bursting exhibits two different ISIs.

Fig.  1. Spike trains of the coexisting bursting of the Chay model when VC = 308.1. (a) Period-1 bursting; eight dots labeled by ai (i = 1, 2, … , 8) are initial values of period-1 bursting. (b) Period-2 bursting; eight dots labeled by bi (i = 1, 2, … , 8) are initial values of period-2 bursting.

Bifurcation of ISI with respect to VC is shown in Fig.  2. As VC increases, period-2 bursting transforms to period-1 bursting at VC = 309.78. As VC decreases, period-1 bursting transforms to period-2 bursting at VC = 307.95. VC∈ [307.95, 309.78] is the region where period-1 and period-2 bursting coexist. When VC is within this range, the Chay model exhibits either period-1 bursting or period-2 bursting; the choice depends on the initial values of (V, n, C). When VC > 309.78, the behavior is mono-stable period-1 bursting. When VC < 307.95, the behavior is mono-stable period-2 bursting.

Fig.  2. Bifurcation of ISIs with respect to VC of the Chay model.

2.3. The attraction domain

Because the attraction domain in the three-dimensional space (V, n, C) is difficult to visualize, we use the attraction domain in a two-dimensional cross-section (V, C) at a fixed n value which is easier to view. As shown in Figs.  3(a)– 3(c), when VC = 308.1, the attraction domain of period-1 bursting (black) and of period-2 bursting (white) in the (V, C) plane, corresponds to n = 0.25, 0.15, 0.3, respectively. The attraction domains in the (V, C) plane corresponding to n = 0.25, 0.15, 0.3, when VC = 309.75 are shown in Fig.  3(d)– 3(e), respectively. The ranges of V and C in Fig.  3(a) and Fig.  3(d) are much larger than in the other four figures. The ranges of V and C of Figs.  3(b)– 3(c) and Figs.  3(e)– 3(f) nearly equal those of the stable period-1 and period-2 bursting patterns. As can be seen from Fig.  3, as VC increases, the black area increases while the white area decreases, thus showing that the attraction domain of period-1 bursting increases while that of period-2 bursting decreases.

Fig.  3. The two-dimensional cross-section in the (V, C) plane of three-dimensional attraction domain of the coexisting period-1 bursting (black) and period-2 bursting (white) at different n value with different VC. VC = 308.1: (a) n = 0.25; (b) n = 0.15; (c) n = 0.3. VC = 309.75: (d) n = 0.25; (e) n = 0.15; (f) n = 0.3.

3. Coupled neuronal model and criteria for synchronization
3.1. Coupled neuronal model

The coupled system is constructed by two bi-directionally coupled identical Chay neurons with a gap junction, [43] which is an important coupling manner that encourages synchrony.[44] The equations of the coupled system are as follows:

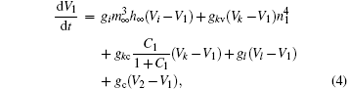
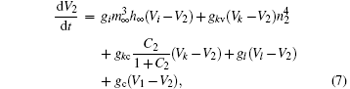
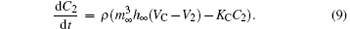
Here, the subscripts 1 and 2 indicate neurons 1 and 2, respectively. The parameter gc is the coupling strength. It varies from 0 to 35 in steps of 0.01. The values of other parameters are the same as those of a single neuron. The coupling item of neuron 1 is gc(V2− V1). The equations are solved numerically using the fourth-order Runge– Kutta integration method with integration time step of 0.001  sec.

3.2. Values of parameter VC

Two values of VC within the coexistence region are chosen, indicated by two arrows in Fig.  2. One is 308.1  mV, which is close to the mono-stable period-2 bursting. The other is 309.75  mV, which is close to the mono-stable period-1 bursting.

3.3. Initial values

When VC = 308.1, eight initial values with equal intervals spanning both period-1 bursting and period-2 bursting, as indicated by dots in Figs.  1(a) and 1(b), are numbered as ai and bi (i = 1, 2, … , 8), respectively, from left to right. For the configuration when one neuron has period-1 bursting and the other period-2 bursting, the 64 initial values aibj (i = 1, 2, … , 8; j = 1, 2, … , 8) are different. For the configuration when both neurons show period-1 bursting, one can ignore the case of i = j (i = 1, 2, … , 8) that lead to coupling-independent compete synchronization and the case of symmetry of i and j; then there are (64− 8)/2 = 28 different initial values aiaj (i = 1, 2, … , 7; j = i+ 1, … , 8). Similarly, there are 28 different bibj (i = 1, 2, … , 7; j = i+ 1, … , 8) values for configuration of when both neurons show period-2 bursting. Thus, a total of 120 (64 + 28 + 28) different initial values are used for VC = 308.1.

Similarly, 120 different initial values are also used for VC = 309.75.

3.4. Criteria for synchronization

We investigate complete synchronization and phase synchronization. Both spike and burst phase synchronizations are considered. The spike phase function (ϕ l(t)) of the firing pattern of neuron l (l = 1, 2) can be defined as follows:

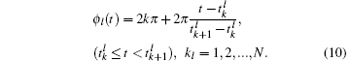
Here, 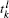is the time of the kth spike of neuron l (l = 1, 2), and N is the number of spikes. The spike phase difference (Δ ϕ (t)) between two coupled neurons is defined as Δ ϕ (t) = |ϕ 1(t) − ϕ 2(t)|. Different spike phase synchronization states can be distinguished by the maximum value of Δ ϕ (t), labeled as max(Δ ϕ (t)), shown as follows:

(i) The complete synchronization (CS) state when max(Δ ϕ (t)) = 0.

(ii) The spike phase synchronization (SS) state when 0 < max(Δ ϕ (t)) ≤ 2π .

(iii) Non-spike phase synchronization state when max(Δ ϕ (t)) > 2π .

When the behavior of the two coupled neurons exhibits non-spike phase synchronization, the burst spike synchronization is considered. The burst phase function (Φ l(t)) of firing pattern of neuron l (l = 1, 2) can be defined as follows:

Here, 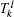is the time of the first spike of the kth burst of neuron l (l = 1, 2), and M is the number of the bursts. The burst phase difference between two coupled neurons is defined as Δ Φ (t) = |Φ 1(t) − Φ 2(t)|. Burst phase synchronization is characterized by the maximum value of Δ Φ (t) labeled max(Δ Φ (t)) as follows:

(1) Burst phase synchronization (BS) state when 0 < max(Δ Φ (t)) ≤ 2π .

(2) Non-burst phase synchronization (NS) state when max(Δ Φ (t)) > 2π .

In addition, lag synchronization (LS) is also considered for some firing patterns. Spike trains of neuron 1 and neuron 2 overlap for LS of firing patterns if one neuron moves forward or backward along time axis and the other remains fixed.

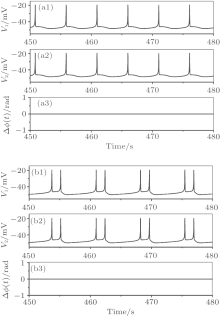
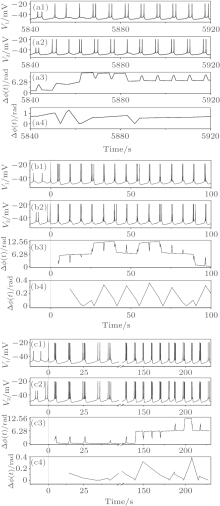
4. Synchronization states and the firing patterns
4.1. Complete synchronization (CS)

CS of period-1 bursting and period-2 bursting can be simulated, as shown in Fig.  4. For example, spike trains of, period-1 bursting of CS are shown in the upper two rows of Fig.  4(a) for the conditions when VC = 309.75, initial value b5b6, and gc = 5.0. The spike trains of period-2 bursting of CS are shown in the upper two rows of Fig.  4(b) for the conditions when VC = 308.1, a1b2, and gc = 4.0. The spike phase differences of both bursting patterns equal zero, as shown in the bottom row of Figs.  4(a) and 4(b).

Fig.  4. The complete synchronization. (a) Period-1 bursting; (b) period-2 bursting. From top to bottom: spike train of neuron 1, spike train of neuron 2, and spike phase difference (Δ ϕ (t)) between neurons 1 and 2.

4.2. Spike phase synchronization (SS)

Spike phase synchronization (SS) can be simulated and the corresponding firing patterns include various periodic and chaotic bursting patterns.

4.2.1. Periodic bursting patterns

A period-3 bursting (VC = 308.1, initial value a1b2, and gc = 1.08) is shown in Fig.  5(a), containing one burst per period and three spikes per burst. A period-(3, 3) bursting (VC = 308.1, initial value a1b2, and gc = 1.3) is illustrated in Fig.  5(b), composed of two bursts per period and three spikes in the both bursts. The ISIs of the three spikes in the first burst are different from those of the second. A period-(7, 8) bursting (VC = 308.1, initial value a1b2, and gc = 3.3) is shown in Fig.  5(c), containing two bursts per period. One burst contains seven spikes and the other eight spikes. In addition, period-k (k = 2, 4) bursting, period-(k, k) (k = 2, 4, 5, 6) bursting and period-(k, k + 1) (k = 2, 3, 4, 5, 6) bursting are simulated.

Fig.  5. Spike phase synchronization of periodic bursting. (a) Period-3 bursting; (b) period-(3, 3) bursting; (c) period-(7, 8) bursting. From top to bottom: spike train of neuron 1, spike train of neuron 2, and spike phase difference between neurons 1 and 2.

For the period-k (k = 2, 3, 4) bursting and period-(k, k) (k = 2, 3, 4, 5, 6) bursting, spikes in the two firing trains within the same time duration exhibit one-to-one correspondence, so max(Δ ϕ (t)) is less than 2π , as shown in the lowest row of Figs.  5(a) and 5(b). For period-(k, k + 1) bursting (k = 2, 3, 4, 5, 6), the burst with k spikes of one neuron corresponds to the burst with k + 1 spikes of the other neuron. The max(Δ ϕ (t)) almost approaches but remains below 2π (bottom row of Fig.  5(c)). All of the above results show that the periodic bursting events are in the SS state.

4.2.2. Chaotic bursting patterns

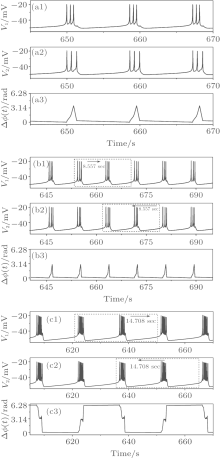
Chaotic bursting patterns include chaos-2 bursting and chaos-(1, 2) bursting. Chaos-2 bursting is composed of bursts with two spikes. Chaos-(1, 2) bursting is composed of bursts containing one spike or two spikes. An example of chaos-2 bursting (VC = 308.1, initial value a1b2, and gc = 0.45), and an example of chaos-(1, 2) (VC = 309.75, initial value a5a7, and gc = 0.01) are shown in Figs.  6(a) and 6(b), respectively. The largest Lyapunov exponents (LEs) of the two firing patterns are 0.58 and 0.26 greater than 0, respectively. The chaos-(1, 2) bursting manifests behaviors that jump between the two coexisting attractors, which is similar to the behaviors that jump between two coexisting chaotic attractors in a previous study.

Fig.  6. Spike phase synchronization of chaotic bursting. (a) Chaos-2 bursting; (b) chaos-(1, 2) bursting. From top to bottom: spike train of neuron 1, spike train of neuron 2, and spike phase difference between neurons 1 and 2.

For the chaos-2 bursting, the max(Δ ϕ (t)) is bounded within 2π due to one-to-one correspondence between spikes from the two neurons. For the chaos-(1, 2) bursting, bursts with one spike appear continuously and are interrupted by single bursts with two spikes. Bursts with two spikes do not appear continuously. The max(Δ ϕ (t)) is less than 2π .

4.3. Burst phase synchronization (BS)

Bursting patterns of BS include three types: another kind of chaos-(1, 2) bursting, chaos-(2, 3) bursting composed of bursts with 2 and 3 spikes, and chaos-(2, k, k + 1) (k = 3, 4) bursting composed of bursts with 2, k, and k + 1 spikes. A chaos-(1, 2) bursting (VC = 309.75, initial value a5a7, and gc = 0.11), a chaos-(2, 3) bursting (VC = 308.1, initial value a1b2, and gc = 0.82), and a chaos-(2, 3, 4) bursting (VC = 308.1, initial value a1b2, and gc = 1.70) are shown in Figs.  7(a)– 7(c), respectively.

The three firing patterns show non-spike synchronization, as shown by the third row of Figs.  7(a)– 7(c). As can be seen from the second burst to the fourth burst of Fig.  7(a), three spikes appear in neuron 1 and five spikes appear in neuron 2. A procedure changing from uncoupling to coupling of the behaviors of the two neurons is shown in Fig.  7(b). Neurons 1 and 2, when isolated (before t = 0  s), exhibit period-1 bursting and period-2 bursting, respectively. The two neurons are coupled together at t = 0  s. Then, two coupled neurons immediately exhibit non-spike phase synchronization but burst phase synchronization of bursting pattern with two or three spikes. Some bursts with two spikes of one neuron may correspond to the bursts with three spikes of the other neuron. For example, there are three spikes in the first and fourth bursts of neuron 1 while there are two spikes in the two bursts of neuron 2. The spike phase difference exceeds 2π . The evolvement of chaos-(2, 3, 4) and changes of phase difference with varying time are illustrated in Fig.  7(c). Different from Fig.  7(b), the spike phase synchronization lasts about 180  s before changing to non-spike synchronization but burst synchronization. Within the 180  s, the spike phase difference less than π lasts about 150  s at first, and then changed to a value between π and 2π .

For the three chaotic firing patterns, bursts from two firing trains within the same time span exhibit a one-to-one correspondence, so the max(Δ Φ (t)) is less than 2π , as shown in the lowest row of Figs.  7(a)– 7(c).

4.4. Non-burst phase synchronization (NS)

A chaos-(1, 2) bursting when VC = 309.75, initial value a3b1, and gc = 0.08 is shown in Fig.  8. When time falls between 2410 and 2480 s (Fig.  8(a)), the number of spikes of neuron 1 is 18, while that of neuron 2 is 15. When time falls between 2017 and 2120  s (Fig.  8(b)), there are 17 bursts for neuron 1 and 19 bursts for neuron 2. Both Δ ϕ (t) and Δ Φ (t) are larger than 2π , showing that the bursting pattern is non-spike or non-burst phase synchronization.

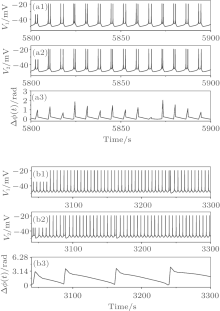
Fig.  7. Burst phase synchronization. (a) Chaos-(1, 2) bursting; (b) from burstings of two isolated uncoupling neurons to chaos-(2, 3) bursting of coupled neurons; (c) from burstings of two isolated uncoupling neurons to chaos-(2, 3, 4) bursting of coupled neurons. Dashed lines in (b) and (c) represent the time of coupling strength changed from 0 to a nonzero value. From top to bottom: spike train of neuron 1, spike train of neuron 2, spike phase difference (Δ ϕ (t)), and burst phase difference (Δ Φ (t)).

4.5. Lag synchronization (LS)

Period-(k, k) (k = 2, 3, 4, 5, 6) and period-(k, k + 1) (k = 2, 3, 4, 5, 6, 7) bursting with spike phase synchronization are also identified as lag synchronization. For instance, the spike trains of neuron 1 and neuron 2 can overlap if one of the spike trains is moved along the time axis and the other is fixed, as shown by the dashed boxes and arrows in Figs.  5(b) and 5(c). The time difference between two spike trains is also shown in the figures.

4.6. Summary of the synchronization states

Different synchronization states and the corresponding firing patterns are summarized in Table  1.

Fig.  8. Non-burst phase synchronization. Chaos-(2, 3) bursting when VC = 309.75mV, initial value a3b1, and gc = 0.08; (a) Time is between 2410 sec and 2480 sec; upper: spike train of neuron 1; middle: spike train of neuron 2; lower: spike phase difference (Δ ϕ (t)); (b) time is between 2017 sec and 2047 sec; upper: spike train of neuron 1; middle: spike train of neuron 2; lower: burst phase difference (Δ Φ (t)).

Table 1. The correspondence between synchronization states and bursting patterns.
5. Transitions between synchronization states

As gc increases, the two coupled neurons achieve complete synchronization states via a complex processes composed of different synchronization states. For convenience, the transitions between synchronization states with increasing gc is called a synchronization transition process in the present paper. The dependence of parameter VC and the initial values on the transition processes are investigated. One hundred and twenty initial values are considered for both VC = 308.1 and VC = 309.75.

5.1. Synchronization transitions when VC = 308.1
5.1.1. Basic structure of the transitions

The transitions with an initial value a1b2 is shown in Fig.  9. The ISIs of neurons 1 and 2 are shown in Figs.  9(a) and 9(b), respectively. According to the maximum values of spike and burst phase difference shown in Figs.  9(c) and 9(d), the transitions are divided into three parts, as labeled by vertical bold dashed lines. Part 1 exhibits transitions between SS and BS (gc < 2.19). Part 2 manifests transitions between SS and CS (gc ∈ [2.19, 3.32]). Part 3 is the CS state (gc > 3.32).

Fig.  9. Transitions with respect to gc, when VC = 308.1 and initial value a1b2. (a) ISIs of neuron 1; (b) ISIs of neuron 2; (c) maximum spike phase difference max(Δ ϕ (t)); (d) maximum burst phase difference max(Δ Φ (t)).

5.1.2. Part 1 of the synchronization transitions

Figure  10(a) is an enlargement of part 1 in Fig.  9(a). The SS and BS transit four times. The four SS states exist in ranges of gc ∈ [0.01, 0.81], [0.83, 1.11], [1.22, 1.67], and [1.73, 2.17], respectively, and the ranges of the four BS states aregc = 0.82, [1.12, 1.21], [1.68, 1.72], and 2.18, respectively. According to the largest Lyaponov exponent (LE) shown in Fig.  10(b), the BS is identified as chaos synchronization and most of the SS is period synchronization with exception of the chaos-2 bursting at gc ∈ [0.43, 0.49]. The transition between BS and SS is also the transition between chaos synchronization and period synchronization.

Fig.  10. Part 1 of the transitions of neuron 1 when VC = 308.1. (a) The transitions with initial value a1b2; (b) the largest Lyapunov exponent correspond to the transitions with initial value a1b2; (c) the transitions with initial value a7a8. The characters “ p” and “ c” are abbreviations of “ period” and “ chaos, ” respectively.

As gc increases, the bursting patterns appear in the following order: period-2, chaos-2, period-(2, 2), chaos-(2, 3), period-(2, 3), period-3, chaos-(2, 3), period-(3, 3), period-(3, 4), period-4, chaos-(2, 3, 4), period-(4, 4), period-(4, 5), and chaos-(2, 4, 5), as shown in Fig.  10(a). The largest number of spikes within a burst of bursting patterns of spike and burst synchronization increases with increasing gc.

The detailed transitions of part 1 in Fig.  9 is not very sensitive to the initial values. The 120 transition processes corresponding to different initial values exhibit almost the same transition processes as shown in Fig.  10(a). For instance, a transition process with initial value a7a8, exhibit almost the same process as the one with initial value a1b2, as shown in Fig.  10(c). The difference between the two processes is described as follows. As shown in Fig.  10(a), the period-(3, 3) bursting appears when gc ∈ [1.22, 1.45] and period-(3, 4) appears when gc∈ [1.46, 1.66]; figure  10(c) shows that the period-(3, 3) bursting appears when gc ∈ [1.22, 1.48] and period-(3, 4) appears when gc ∈ [1.49, 1.66]. The processes within the remaining ranges of gc shown in Fig.  10(a) are the same as those shown in Fig.  10(c).

5.1.3. Part 2 of the synchronization transitions

Part 2 of the process shown in Fig.  9(a) is highlighted in Fig.  11(a). The right boundary is at gc = 3.32. The transition between CS state and SS state happens three times. The ranges of the three CS states are gc∈ [2.19, 2.43], [2.61, 2.84], and [2.99, 3.23] and of the three SS states aregc∈ [2.44, 2.60], [2.85, 2.98], and [3.24, 3.32]. Asgc increases, ignoring the period-2 bursting of CS, the following types appear in order: period-(5, 5), period-(5, 6), period-(6, 6), period-(6, 7), and period-(7, 8) bursting of SS. The period-(7, 8) bursting is the final bursting. This shows that the largest number of spikes within a bursting pattern of SS increases with increasing gc.

Fig.  11. Part 2 of the transitions of neuron 1 when VC = 308.1. (a) The transitions with initial value a1b2; (b) the transitions with initial value a7a8; (c) dependence of the 120 initial values. The characters “ p” and “ c” are abbreviations of “ period” and “ chaos, ” respectively.

Part 2 of the process with initial values a7b8 is shown in Fig.  11(b). The right boundary is at gc = 2.60. The transition between the CS state and SS state happens only once. The difference between these two transition processes with initial values a1b2 and a7a8 indicates that the detailed process is sensitive to initial values. The right boundary and times of transitions between SS and CS depend on the initial values.

Figure  11(c) illustrates the dependence of 120 initial values on the detailed processes. There are 68 processes that transit three times, and the right boundary of gc is between 3.23 and 3.33. Twenty-three processes transit two times, and gc of the right boundary is between 2.83 and 3.03. Twenty-two processes transits one time, and the gc values of the right boundary are between 2.38 and 2.63. The remaining seven processes achieve the CS states of period-2 bursting that remains unchanged as gc increases and do not experience transition.

5.1.4. Part 3 of the synchronization transitions

Part 3 of the process is in the CS state and is also sensitive to the initial values. The left boundary of gc for part 3 depends on the right boundary of part 2. Out of the 120 processes 109 exhibit CS of period-2 bursting, which remains unchanged as gc increases, as shown in Fig.  9(a); the remaining 11 processes manifest a transition from period-2 bursting to period-1 bursting of CS, which remains unchanged as gc increases. This is shown in Fig.  12. Table  2 summarizes the details of how the bursting patterns of CS depend on the initial values. The results show that most initial values lead to period-2 bursting of CS, while only a few lead to period-1 bursting.

Table 2. The number of bursting patterns of complete synchronization when VC = 309.75.

Fig.  12. Part 3 of the transitions when VC = 308.1 and initial value a8b7.

5.2. Synchronization transitions when VC = 309.75
5.2.1. Basic structure of transitions

A detailed transition processes with initial value b5b6 can be divided into four parts labeled by the bold vertical dashed lines in Fig.  13. Part 1 is almost in the non-burst synchronization (NS) state. Part 2 exhibits transitions between SS and BS states. Part 3 manifests transitions between SS and CS states. Part 4 is the CS state.

Fig.  13. Transitions with respect to gc, when VC = 309.75 and initial value b5b6. (a) ISIs of neuron 1; (b) ISIs of neuron 2; (c) maximum spike phase difference max(Δ ϕ (t)); (d) maximum burst phase difference max(Δ Φ (t)).

5.2.2. Part 1 of the synchronization transitions

Part 1 exhibits the NS state of chaos-(1, 2) bursting (Fig.  8) when gc < 0.12, with three exceptions: gc = 0.01, 0.03, and 0.11. When gc = 0.01 and 0.03, the chaos-(1, 2) bursting is in the SS state (Fig.  6(b)). When gc = 0.11, the chaos-(1, 2) bursting exhibit BS (Fig.  7(a)). This part is insensitive to the initial value.

5.2.3. Part 2 of the synchronization transitions

Figures  14(a) and 14(b) are enlargement of part 2 from Fig.  13(a) as well as the largest Lyapunov exponent (LE) of neuron 1. The transition between SS and BS states happen three times when gc∈ [0.12, 1.70]. These transitions also represent the transitions between chaos and period synchronizations. The ranges of the three SS states are gc∈ [0.12, 0.82], [0.84, 1.12], and [1.22, 1.69], and those of the three BS states aregc = 0.83, [1.13, 1.21], and 1.70. As gc increases, period-2, chaos-2, period-(2, 2), chaos-(2, 3), period-(2, 3), period-3, chaos-(2, 3), period-(3, 3), period-(3, 4), period-4, and chaos-(2, 3, 4) bursting appear in order.

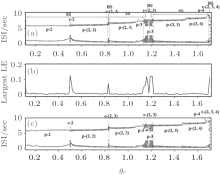Fig.  14. Part 2 of the transitions of neuron 1 when VC = 309.75. (a) The transitions with initial value b5b6; (b) the largest Lyapunov exponent correspond to the transitions with initial value b5b6; (c) the transitions with initial value a3b1. The characters “ p” and “ c” are abbreviations of “ period” and “ chaos, ” respectively.

The process with initial value a3b1 is shown Fig.  14(c). This exhibits almost the same process as that shown in Fig.  14(a), showing that the detailed process of part 2 is insensitive to the initial values. The small difference between the processes shown in Figs.  14(a) and 14(c) is not addressed in this paper. All 120 transition processes exhibit almost the same process.

5.2.4. Part 3 of the synchronization transitions

Part 3 of the process shown in Fig.  13(a) and that of neuron 1 with initial value a3b1 are shown in Figs.  15(a) and 15(b), respectively. The gc values of right boundary and the times of transition between SS and CS are different. For example, the right boundary of Figs.  15(a) and 15(b) are gc = 2.96 and gc = 3.30, respectively.

Figure  15(c) shows how part 3 of the 120 processes depends on initial values. The gc values of the right boundary of 70 processes are between 3.26 and 3.34, and transit 4 times between SS and CS. Seventeen processes transit three times, and gc of the right boundary is between gc = 2.86 and 3.01. Twenty-five processes transit two times, and the gc value corresponding to the right boundary is between 2.26 and 2.63. Six processes transit one time, and gc of the right boundary is between 1.89 and 2.19. The remaining two processes achieve the CS of period-2 bursting that remains unchanged as gc increases and do not transit.

Fig.  15. Part 3 of the transitions of neuron 1 when VC = 309.75. (a) The transitions with initial value b5b6; (b) the transitions with initial value a3b1; (c) dependence of the 120 initial values. The characters “ p” and “ c” are abbreviations of “ period” and “ chaos, ” respectively.

5.2.5. Part 4 of the synchronization transitions

Part 4 of the process is the CS state. This part is also sensitive to the initial value. Ninety-five out of the 120 process transit from period-2 bursting to period-1 bursting of CS, which remains unchanged as gc increases. One example of this case is shown in Fig.  13(a). Two processes manifest the CS of period-1 bursting, which remains unchanged as gc increases. The remaining 23 initial values lead to CS of period-2 bursting, which also remains unchanged as gc increases, as shown in Fig.  16.

Fig.  16. Part 4 of the transitions when VC = 309.75 and initial value a3b1.

The number of initial values that lead to unchanged period-1 bursting and period-2 bursting of CS is shown in Table  3. When VC = 309.75, most initial values lead to period-1 bursting of CS, while only a few lead to period-2 bursting, which is just the opposite of the result when VC = 308.1. This is consistent with attraction domains to a certain extend. When VC = 308.1, the attraction domain of period-2 bursting is much bigger than that of the period-1 bursting. When VC = 309.75, the attraction domain of period-1 bursting increases.

Table 3. Number of bursting patterns of complete synchronization when VC = 308.1.
5.3. Difference between processes with different parameter values of VC

Three differences are extracted by comparing the transition processes of VC = 308.1 and 309.75. First, a NS state exists in the transition process of VC = 309.75; while no NS state exist in the transition process of VC = 308.1. Second, the minimum coupling strength for CS of network with VC = 309.75 (gc = 1.71) is lower than that of network with VC = 308.1 (gc = 2.19). Third, when VC = 308.1, the network is more likely to achieve the CS of period-2 bursting that corresponds to large gc. When VC = 309.75, the network is more likely to achieve CS of period-1 bursting.

5.4. Cause of the increase in the number of spikes within a burst

The increase in the maximum number of spikes within a burst with gc increasing can be interpreted by the coupling item. For example, the number of spikes within a burst of neuron 1 when VC = 308.1 and initial value a1b2 is shown in Fig.  17(a). Correspondingly, the maximum values (Fig.  17(b)) of the coupling item of neuron 1 increase and the minimum values (Fig.  17(c)) decrease as gc increases. This is consistent with the fact that the stronger the stimulus (i.e., the coupling in this condition) to the neuron, the more spikes there are within the burst.

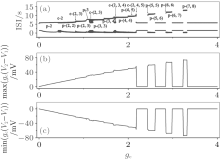Fig.  17. (a) The transitions of neuron 1 when VC = 308.1 and initial value a1b2; (b) maximum value of the coupling item of neuron 1; (c) minimum value of the coupling item of neuron 1. The characters “ p” and “ c” are abbreviations of “ period” and “ chaos, ” respectively.

6. Conclusions and discussion

Recently, the spike and burst synchronization and the transition from the burst synchronization to the spike synchronization have been widely investigated.[17– 22] In this paper, the Chay model shows that period-1 bursting and period-2 bursting coexist within a parameter range, and the coexisting behavior lies between mono-stable period-1 and period-2 bursting. As VC increases, the attraction domain of period-1 bursting increases while that of the coexisting period-2 bursting decreases. Various synchronization states, including complete synchronization, spike phase synchronization, burst phase synchronization, lag synchronization, and non-synchronization, are simulated in a network constructed by two bi-directionally coupled Chay model neurons with coexisting period-1 and period-2 bursting. The burst phase synchronization is identified as chaos synchronization and spike phase synchronization as synchronization of periodicity.

With increasing coupling strength gc, the coupled neurons can achieve complete synchronization states via complex processes. The process depends on the parameter values within the coexisting parameter region and on the initial values. When the coexisting behavior is near period-1 bursting, the process can be divided into four parts. Part 1 is the non-synchronization. Part 2 represents the transitions between burst phase and spike phase synchronization. The processes of part 1 and part 2 are insensitive to initial values. Part 3 represents the transitions between spike phase and complete synchronization. The transit times and range of gc depend on initial values. Part 4 represents complete synchronization. Most initial values lead to complete synchronization of period-1 bursting and fewer initial values lead to complete synchronization of period-2 bursting when gc is large enough. When the coexisting behavior is near the period-2 bursting, three parts similar to parts 2, 3, and 4 are simulated. Most initial values lead to complete synchronization of period-2 bursting and fewer initial values lead to complete synchronization of period-1 bursting when gc is large enough. The increase of the probability that CS of period-1 bursting will be achieve is, to a certain extent, consistent with the increase of attraction domain of period-1 bursting. The dependence of the transitions on the parameter values is consistent with the results of a previous study.[37] The synchronization transitions of this paper show more complex characteristics than those in previous works.[31– 38] The most important finding of this paper is the sensitivity of the process to the initial values, especially for those transitions between spike phase and complete synchronization and for the complete synchronization. The dependence of the process on initial values was given little attention in previous works.[31– 38] The synchronization processes that are complex, show a dependence on the initial values and parameters, contain transitions between spike and burst synchronization and between phase and complete synchronization, and chaos synchronization are all helpful to understand the complex spatiotemporal behaviors of networks[45– 51] and synchronization transitions in the nervous system.[31– 38]

The burst synchronization was found to be a chaos synchronization. This shows that chaos synchronization can be caused by cooperation between neurons with periodic behaviors. The transition between spike and burst phase synchronization states also illustrate the transition between chaos synchronization and synchronization of periodic behaviors. When the coexisting behavior is near mono-stable period-1 bursting, we simulate the non-synchronization of bursting pattern at small coupling strength. The behavior of the non-synchronization state jumps between the coexisting attractors, which is similar to the asynchronous synchronization reported in a previous work.[31]

The number of spikes per burst of non-complete synchronous bursting increases with increasing coupling strength. This shows that bursting with multiple spikes per burst can be caused by the cooperation between neurons with one or two spikes per burst. Physiologically, bursting patterns with multiple spikes per burst can often be recorded by neurons of the central nervous system.[12, – 16] The results in this paper indicate that the physiologically recorded bursting with multiple spikes per burst may originate from cooperation between neurons.

From the results of the related investigations[31– 38] and this paper, we conclude that the transitions from non-synchronization to complete synchronization with increasing coupling strength, which depends on parameter values and initial values, can be simulated in the coupled systems. These systems show multi-stable or coexisting behaviors when isolated. Various detailed characteristics are shown for specific networks with coexisting behaviors.[31– 38] In the future, more investigations should be performed to reveal more general dynamics of network with coexisting behaviors. The structure of the attraction domain may be helpful to understand the complex transitions. In Ref.  [37], the attraction domain is continuous and no chaos synchronization appears. In the present paper, the attraction domain shows a discrete structure or possible fractal structure. In addition, the transitions in Ref.  [37] looks simpler than those in the present paper. Combining the trajectory of the coupled system and the attraction domain may be helpful to further identify the dynamics of the complex transitions.

Reference
1 Arenas A, Díaz-Guilera A, Kurths J, Moreno Y and Zhou C S 2008 Phys. Rep. 469 93 DOI:10.1016/j.physrep.2008.09.002 [Cited within:2] [JCR: 22.929]
2 Glass L 2001 Nature 410 27 DOI:10.1038/35065186 [Cited within:1] [JCR: 38.597]
3 Pecora L M and Carroll T L 1990 Phys. Rev. Lett. 64 821 DOI:10.1103/PhysRevLett.64.821 [Cited within:1] [JCR: 7.943]
4 Singer W and Gray C M 1995 Annu. Rev. Neurosci. 18 555 DOI:10.1146/annurev.ne.18.030195.003011 [Cited within:2] [JCR: 20.614]
5 Llináas R and Ribary U 1993 Proc. Natl. Acad. Sci. USA 90 2078 DOI:10.1073/pnas.90.5.2078 [Cited within:1]
6 Hartline D K 1979 Biol. Cybern. 33 223 DOI:10.1007/BF00337410 [Cited within:1] [JCR: 2.067]
7 Kim K H, Yoon J, Kim J H and Junq K Y 2008 Brain Res. 1236 105 DOI:10.1016/j.brainres.2008.07.118 [Cited within:1] [JCR: 2.879]
8 Choi J W, Jung K Y, Kim C H and Kim K H 2010 Neurosci. Lett. 468 156 DOI:10.1016/j.neulet.2009.10.088 [Cited within:1] [JCR: 2.026]
9 Bartsch R, Kantelhardt J W, Penzel T and Havlin S 2007 Phys. Rev. Lett. 98 54102 DOI:10.1103/PhysRevLett.98.054102 [Cited within:1] [JCR: 7.943]
10 Buzsáaki G and Draguhn A 2004 Science 304 1926 DOI:10.1126/science.1099745 [Cited within:1]
11 Gray C M, Köonig P, Engel A K and Singer W 1989 Nature 338 334 DOI:10.1038/338334a0 [Cited within:1] [JCR: 38.597]
12 Jefferys J G and Haas H L 1982 Nature 300 448 DOI:10.1038/300448a0 [Cited within:2] [JCR: 38.597]
13 Kepecs A, Wang X J and Lisman J 2002 J. Neurosci. 22 9053 [Cited within:1] [JCR: 6.908]
14 Kepecs A and Lisman J 2003 Network 14 103 DOI:10.1080/net.14.1.103.118 [Cited within:1]
15 Sun X J, Lei J Z, Perc M, Kurths J and Chen G R 2011 Chaos 21 016110 DOI:10.1063/1.3559136 [Cited within:1] [JCR: 2.188]
16 Ando H, Suetani H, Kurths J and Aihara K 2012 Phys. Rev. E 86 016205 DOI:10.1103/PhysRevE.86.016205 [Cited within:2] [JCR: 2.313]
17 Batista C A, Viana R L, Ferrari F A, Lopes S R, Batista A M and Coninck J C 2013 Phys. Rev. E 87 042713 DOI:10.1103/PhysRevE.87.042713 [Cited within:2]
18 Gu H G, Pan B B and Xu J 2014 EPL 106 50003 DOI:10.1209/0295-5075/106/50003 [Cited within:1] [JCR: 2.26]
19 Gu H G, Li Y Y, Jia B and Chen G R 2013 Physica A 392 3281 DOI:10.1016/j.physa.2013.03.039 [Cited within:1] [JCR: 1.676]
20 Droz M and Lipowski A 2003 Phys. Rev. E 67 056204 DOI:10.1103/PhysRevE.67.056204 [Cited within:1] [JCR: 2.313]
21 Liang X, Tang M, Dhamala M and Liu Z 2009 Phys. Rev. E 80 066202 DOI:10.1103/PhysRevE.80.066202 [Cited within:1] [JCR: 2.313]
22 Wang Q Y, Chen G R and Perc M 2011 PLoS One 6 e15851 DOI:10.1371/journal.pone.0015851 [Cited within:2] [JCR: 3.73]
23 Ozbudak E M, Thattai M, Lim H N, Shraiman B I and Van Oudenaarden A 2004 Nature 427 737 DOI:10.1038/nature02298 [Cited within:1] [JCR: 38.597]
24 Guttman R, Lewis S and Rinzel J 1980 J. Physiol. 30 377 [Cited within:1]
25 Izhikevich E M 2000 Int. J. Bifurcat. Chaos 10 1171 DOI:10.1142/S0218127400000840 [Cited within:1] [JCR: 0.921]
26 Tateno T and Pakdaman K 2004 Chaos 14 511 DOI:10.1063/1.1756118 [Cited within:1] [JCR: 2.188]
27 Lechner H A, Baxter D A, Clark J W and Byrne J H 1996 J. Neurophysiol. 75 957 [Cited within:1] [JCR: 3.301]
28 Fröohlich F and Bazhenov M 2006 Phys. Rev. E 74 031922 DOI:10.1103/PhysRevE.74.031922 [Cited within:1] [JCR: 2.313]
29 Cymbalyuk G and Shilnikov A 2005 J. Comput. Neurosci. 18 255 DOI:10.1007/s10827-005-0354-7 [Cited within:1] [JCR: 2.439]
30 Xu Y L, Yang M H, Liu Z Q, Liu H J, Gu H G and Ren W 2007 Dyn. Contin. Discrete Impuls. Syst. Ser. B 14 35 [Cited within:1]
31 Pisarchik A N, Jaimes-Reáategui R and García-López J H 2008 Phil. Trans. R. Soc. A 366 459 DOI:10.1098/rsta.2007.2103 [Cited within:8]
32 Pisarchik A N, Jaimes-Reátegui R and García-Ló;pez J H 2008 Int. J. Bifurcat. Chaos 18 1801 DOI:10.1142/S0218127408021385 [Cited within:1] [JCR: 0.921]
33 Pisarchik A N, Jaimes-Reátegui R, Villalobos-Salazar J R, García-Lápez J H and Boccaletti S 2006 Phys. Rev. Lett. 96 244102 DOI:10.1103/PhysRevLett.96.244102 [Cited within:1] [JCR: 7.943]
34 Sausedo-Solorio J M and Pisarchik A N 2011 Phys. Lett. A 375 3677 DOI:10.1016/j.physleta.2011.07.057 [Cited within:1] [JCR: 1.11]
35 Ruiz-Oliveras F R and Pisarchik A N 2009 Phys. Rev. E 79 016202 DOI:10.1103/PhysRevE.79.016202 [Cited within:1] [JCR: 2.313]
36 Wang Q Y, Duan Z S, Feng Z S, Chen G R and Lu Q S 2008 Physica A 387 4404 DOI:10.1016/j.physa.2008.02.067 [Cited within:2] [JCR: 1.676]
37 Gu H G, Li Y Y, Jia B and Chen G R 2013 Physica A 392 3281 DOI:10.1016/j.physa.2013.03.039 [Cited within:5] [JCR: 1.676]
38 Bing J 2014 Chin. Phys. B 23 050510 DOI:10.1088/1674-1056/23/5/050510 [Cited within:6] [JCR: 1.148] [CJCR: 1.2429]
39 Chay T R 1985 Physica D 16 233 DOI:10.1016/0167-2789(85)90060-0 [Cited within:2] [JCR: 1.669]
40 Gu H G 2013 Chaos 23 023126 DOI:10.1063/1.4810932 [Cited within:1] [JCR: 2.188]
41 Gu H G and Xiao W W 2014 Int. J. Bifurcat. Chaos 24 1450082 DOI:10.1142/S0218127414500825 [Cited within:1] [JCR: 0.921]
42 Gu H G, Ren W, Lu Q S, Wu S G and Chen W J 2001 Phys. Lett. A 285 63 DOI:10.1016/S0375-9601(01)00278-X [Cited within:1]
43 Hestrin S and Galarreta M 2005 Trends Neurosci. 28 304 DOI:10.1016/j.tins.2005.04.001 [Cited within:1] [JCR: 13.582]
44 Chow C and Kopell N 2000 Neural Comput. 12 1643 DOI:10.1162/089976600300015295 [Cited within:1] [JCR: 1.76]
45 Wang H J, Huang H B and Qi G X 2005 Phys. Rev. E 72 037203 DOI:10.1103/PhysRevE.72.037203 [Cited within:1] [JCR: 2.313]
46 Pikovsky A, Zaks M, Rosenblum M, Osipov G and Kurths J 1997 Chaos 7 680 DOI:10.1063/1.166265 [Cited within:1] [JCR: 2.188]
47 Chen J Y, Wong K W and Shuai J W 2002 Phys. Rev. E 66 056203 DOI:10.1103/PhysRevE.66.056203 [Cited within:1] [JCR: 2.313]
48 Taherion S and Lai Y C 1999 Phys. Rev. E 59 6247 DOI:10.1103/PhysRevE.59.R6247 [Cited within:1] [JCR: 2.313]
49 Corron N J, Blakely J N and Pethel S D 2005 Chaos 15 023110 DOI:10.1063/1.1898597 [Cited within:1] [JCR: 2.188]
50 Wu X and Ma J 2013 PLoS One 8 e55403 DOI:10.1371/journal.pone.0055403 [Cited within:1] [JCR: 3.73]
51 Ma J, Huang L, Wang C N and Pu Z S 2013 Commun. Theor. Phys. 59 233 DOI:10.1088/0253-6102/59/2/16 [Cited within:1]