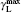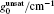†Corresponding author. E-mail: akbar_hariri@yahoo.com
Amplified spontaneous emission (ASE), including intensity and bandwidth, in a typical example of BuEH-PPV is calculated. For this purpose, the intensity rate equation is used to explain the reported experimental measurements of a BuEH-PPV sample pumped at different pump intensities from Ip = 0.61 MW/cm2 to 5.2 MW/cm2. Both homogeneously and inhomogeneously broadened transition lines along with a model based on the geometrically dependent gain coefficient (GDGC) are examined and it is confirmed that for the reported measurements the homogeneously broadened line is responsible for the light–matter interaction. The calculation explains the frequency spectrum of the ASE output intensity extracted from the sample at different pump intensities, unsaturated and saturated gain coefficients, and ASE bandwidth reduction along the propagation direction. Both analytical and numerical calculations for verifying the GDGC model are presented in this paper. Although the introduced model has shown its potential for explaining the ASE behavior in a specific sample it can be universally used for the ASE study in different active media.
Amplified spontaneous emission (ASE) is an interesting phenomenon that has been studied both experimentally and theoretically for many years. From the theoretical point of view we may refer to a number of published papers in this subject, including the earliest papers published by Peters and Allen, [1, 2] Casperson and Yariv, [3] Casperson, [4] and Pert.[5] In recent years, on the other hand, with the emerging need of laser materials for their vast applications in laser technology, conjugated polymer films, BuEH-PPV, [6] MEH-PPV, [7– 9] cyano substituted oligo (CN-DPDSB) single crystal, [10] InAs quantum dots, [11] etc., were studied extensively, where due to their importance, the subject has also been reviewed.[12, 13] The most important interest in these studies is to use ASE as a source of coherent radiation. Experimentally, samples under the study are usually excited by pump lasers with an input laser intensity Ip. The results of the measurements are often introduced by plots of ASE intensity, IASE, and bandwidth, Δ λ ASE, versus sample excitation length, lAMP.
For analyzing the experimental measurements, and particularly to determine the ASE gain coefficient, the experimental data points are commonly fitted to an equation given by,

where g0(λ ) is the small signal gain and A is a constant. By using the intensity rate equation and considering the fact that small-signal gain is z-independent, upon assuming that ASE initiates at one end of the sample; that is, using a boundary condition that the ASE intensity is equal to zero at z = 0, equation (1) can be readily obtained.[14]
On the other hand, a particularly interesting feature of the ASE character is that the ASE spectral line narrows while light propagates along the z direction. The earliest study of explaining the spectral narrowing phenomenon was introduced by Yariv and Leite[15] and more elaborate work appearing in Ref. [3], where some approximations were adopted, showed that at large distances the ASE bandwidth reduction, Δ ν ASE/Δ ν 0, for homogeneously (H) and Doppler (D) broadened line shapes with the ASE bandwidths of Δ ν ASE, H and Δ ν ASE, D are given, respectively, by
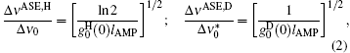
where Δ ν 0 and 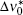



From the theoretical point of view for the behavioral study of the gain coefficient in an OSC– AMP N2-laser system with an amplifier of different excitation lengths, using a mathematical model for N2-lasers as introduced initially by Fitzsimmons et al., [19] we calculated gain coefficients for the AMP section of the laser system for different electrode lengths at instants when the values of gain coefficient, g0(t), were maximal. In this study, we let the cavity lifetime, τ ph, for a traveling wave be some fraction, κ , of lAMP/c, where consequently κ was found to be related to the power loss. c is the light velocity in the medium. With this approach the power loss γ L was introduced into the photon density rate equation. The numerical calculation then showed that γ L is z-dependent and reduces as 
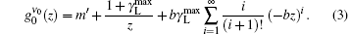
Here, 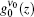
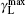
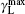
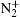
About the study of the ASE phenomenon, on the other hand, for explaining the ASE output energy in a KrF laser, i.e., ε ASE versus lAMP, gain coefficients for different segmented excitation lengths were calculated and it is observed that the calculated ASE gain coefficients also obey an equation similar to Eq. (3). With the available experimental measurements, as specific examples, equation (3) was used to predict the ASE output behavior in KrF[22– 25] and N2[26, 27] lasers, and we found that the corresponding ASE gain profiles, denoted by 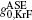
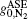

In general, for applying the model of geometrically dependent gain coefficient (GDGC) with a plot of measured ASE output energy or intensity versus excitation length for a given sample, we can obtain gain parameters for the excited sample, and consequently the ASE gain profile, 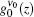
In the present work we use Eq. (3) along with the intensity rate equation to explain the ASE behaviors in organic solid materials theoretically. These materials are prepared in small-sized dimensions. For the study, we include the threshold length zth in our analysis. Although the values of zth are very small in these materials due to their small dimensions, but it is important to take them into consideration in the calculation to obtain a correct prediction for the ASE behavior. In fact, in the reported measurements of organic materials, the presence of the threshold lengths in the experimental measurements is visualized clearly. For verifying the geometrical model of the gain coefficient in small-sized materials, we use the reported measurements of the intensity and ASE bandwidth reduction along the excitation length. For the study of the spectral behavior, by the use of an analytical approach, we find that the output intensity spectrum for ν ∼ ν 0, or x2 ≪ 1, for high pump intensity, Ip, has a Gaussian distribution when initially a homogeneously (H) broadened line shape is used for the calculation. We will show that this condition is also satisfied for long enough excitation lengths when the narrowing of the ASE bandwidth occurs. For x2 ≫ 1, or in the earlier stage of the ASE propagation, the intensity behavior has a Lorentzian frequency distribution. On the other hand, our calculations show that when initially an inhomogeneously or Doppler (D) broadened transition is used, the intensity profiles for both x2 ≪ 1 and x2 ≫ 1 turn out to be Gaussian functions. To observe the details of the bandwidth narrowing, the numerical calculations for the ASE intensities for homogeneously and inhomogeneously broadened line shapes are also carried out. For the analysis that is made for the BuEH-PPV sample, it is determined that a homogeneously broadened transition is responsible for the broadening mechanism. The results indicate that the approach gives excellent consistency with the measurements for the whole range of the sample excitation lengths and for different pumping conditions. In particular, we realize that the saturation effect has an important influence on the analysis. When the saturation effect is introduced in the intensity rate equation, the results of the calculated intensity for H-broadened lines show that when light propagates along the z direction, the intensity profile in a logarithmic scale versus excitation length z, has a sharp and subsequently a smooth bending curvature. Consequently a saturation length, zsat, which refers to a length at which the ASE intensity is equal to the saturation intensity, is defined. In contrast to Eq. (1) that cannot explain the experimental data in the whole range of measurements, fittings of the experimental data, by applying the present model, are found to be well performed. In addition to the unsaturated gain coefficient, 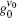
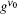
The analytical approach to explain the ASE behavior, using a four level system for a homogeneously broadened transition, has led to an analytical expression for the ASE output energy or intensity, and has been introduced in Refs. [22] and [23]. Thus, the details of this part of the calculation are not given here, except some relevant parts for better understanding of the proposed method. In this work, in addition to extending the analytical considerations for different conditions that appear in experiments, specific attention will be paid to the numerical calculations, and the corresponding results are introduced by graphs and the deduced relevant parameters are tabulated. Comparisons between numerical and analytical results for explaining experimental measurements will be also given to elucidate the ASE behavior in a small-sized sample completely.
For calculating the ASE intensity Iν and bandwidth Δ ν ASE for the steady-state solution, we start with the intensity rate equation when the saturation effect is not included in the rate equation, i.e.,
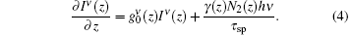
Here, τ sp is the medium upper state radiative lifetime. For a four level system the upper-state population N2(z) is related to the gain coefficient by 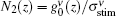
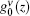
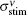
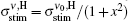
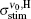


The second term on the right-hand side in Eq. (4) is 

where 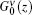
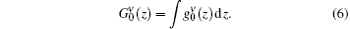
It should be emphasized that at z = zth, the ASE intensity is equal to zero and this constitutes the boundary condition for solving the intensity rate equation.
For the saturation intensity at frequency ν , we can use
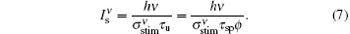
Here, ϕ is the fluorescence quantum yield, given by ϕ = τ u/τ sp, where τ u is the medium upper state lifetime. By introducing 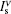

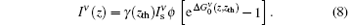
This is the general solution for the ASE intensity at the transition frequency ν . For the z-independent value of 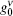



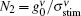
 |
Here, we may define A(ν ) = γ (zth) α absϕ ν /ν p for any transition frequency ν . From Eq. (8a) we finally obtain
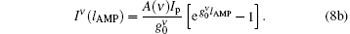 |
It is seen that equation (8b) is the same as Eq. (1) when we let IASE(lAMP) ≡ Iν (lAMP). It is also a simplified form of Eq. (8) on the assumption that the gain coefficient is z-independent. Here, ν = c/λ is also applied.
For applying Eq. (8), two cases for the analytical solution for an H-broadened system may be considered.
Case a For ν ∼ ν 0 so as to obtain the x2 ≪ 1 condition, we can further use Eq. (8) and apply this equation to the H-broadened line transition. In this case, we use symbols of 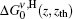


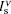
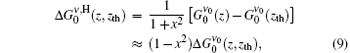
where 

and we also define 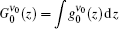

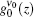
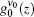

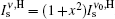


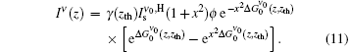
By expanding the second term inside the brackets and upon neglecting the terms with x2, x4, … factors, we obtain finally,
 |
In the plot of Iν (z) versus x for a given z, if the Iν measurements appear to follow Eq. (11a), then one can expect to obtain a Gaussian frequency distribution. By defining the saturation length, zsat, the numerical calculation, in fact, shows that the x2 ≪ 1 condition corresponds to a large z; that is, the condition when z ≫ zsat is satisfied. This refers to the present study of the H-broadening when the total medium is pumped optically with a high pump intensity Ip, where z ≫ zsat is satisfied.
The presence of the 
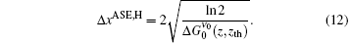
By applying the x = 2(ν − ν 0)/Δ ν 0 to getting Δ xASE, H = 2Δ ν ASE, H/Δ ν 0, we obtain the ASE bandwidth reduction,

where Δ ν 0 is the spontaneous emission bandwidth for the H-broadened line.
By using the gain formulation as given by Eq. (3), and evaluating the 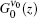
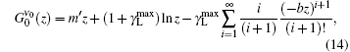
and
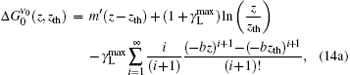 |
from which we finally reach the following analytical expression for the ASE bandwidth reduction along the z direction for the case when z ≫ zsat is satisfied:
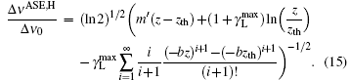
It is interesting to see that by ignoring the last two terms in Eq. (14a), and by letting 
The stimulated emission cross section for the homogeneously broadened line shape at ν = ν 0 is given by 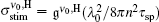

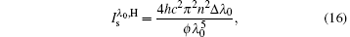
where 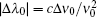
Case b For the x2 ≫ 1 condition, where it also corresponds to the z ≪ zsat condition, say, at the earliest stage of the ASE propagation, we may again use Eq. (8). If we let 
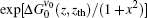
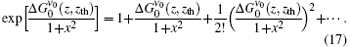
By keeping the first three terms in Eq. (17), and under the condition which is imposed on Eq. (8), then equation (8) is written as

where again 

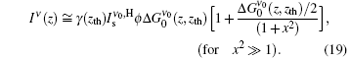
For x → ∞ , we obtain a constant value for Iν (z), which is ν 0-dependent. Here, we can define the expression 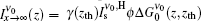
 |
Equation (19a) shows that Iν (z) has a Lorentzian frequency distribution at any distance z if the 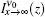
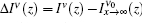
 |
That is, under the condition of x2 ≫ 1, the ASE bandwidth is the same as the spontaneous emission bandwidth.
For a very large x, the FWHM can be obtained from Eq. (19a) analytically when the 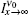
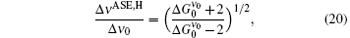
where the 


where ξ = 1/(1 + x2) is defined. For the positive solution of Eq. (21), we obtain

and Δ ν ASE, H/Δ ν 0 is obtained, accordingly,
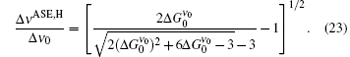
Thus, for the H-broadened transition, we observe that without including the saturation effect, equation (5) or (8) can explain the ASE intensity in general, and at two limits of x2 ≪ 1 and x2 ≫ 1, the analytical solutions as given by Eqs. (11a) and (19a) turn out to be a Gaussian and a Lorentzian frequency distribution, respectively. This prediction will be verified by the experimental measurements and also by the corresponding numerical calculations.
We may apply the previous procedure as given in Subsection 2.1, to the Doppler (D) broadened transition. For the stimulated emission cross section, we have 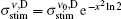
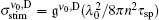

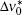

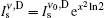

where for 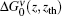

Case (i) For ν ∼ ν 0 or x2 ≪ 1, we can approximate e− x2ln 2 ≈ 1 − x2ln 2, and consequently equation (24) turns out to be
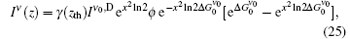
where 



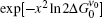
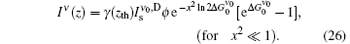
Equation (26) shows that the ASE intensity has a Gaussian frequency distribution for x2 ≪ 1, which will be shown to correspond to the z ≫ zsat condition. The FWHM can be obtained easily from this equation,

By ignoring the last two terms in Eq. (14a) and by letting z− zth = lAMP and 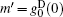
Case (ii) For x2 ≫ 1, i.e., in the earliest stage of the ASE propagation along the z direction, or when z ≪ zsat is satisfied, the first exponential term inside the brackets in Eq. (24) can be expanded to yield
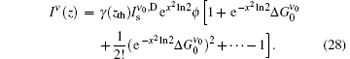
By keeping the first 3 terms in the expansion, we have
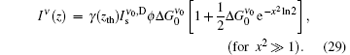
Equation (29) shows that the intensity spectrum again has a Gaussian distribution added to a constant value given by 
 |
which shows that Iν (z) has a Gaussian frequency profile if the 


The introduced analytical expression appearing in these two subsections along with the numerical calculations that will be given in Section 3, are used to explain the experimental observations appearing in the article by McGehee et al.[6] Generally, we learn from Subsections 2.1 and 2.2 that according to the initial frequency distribution of the line-shape, which is either a Lorentzian or a Gaussian function, the ASE intensity distribution for z ≫ zsat (or x2 ≪ 1) has a Gaussian distribution. For z ≪ zsat (or x2 ≫ 1), on the other hand, if we start with a homogeneously broadened transition, the IASE has a Lorentzian line-shape and for an inhomogeneously broadened system IASE has a Gaussian frequency distribution. Thus, with the output spectrum measured at the exit face of a pumped sample, and by knowing the numerical value of zsat one can make an accurate evaluation for the initial frequency distribution for the type of the broadening mechanism involved in the interaction.
We may consider solving the problem numerically, where saturation and frequency dependences of the gain coefficient are taken into account in the intensity rate equation. For this purpose, 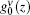
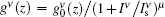
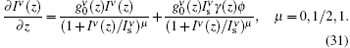
Equation (31) is a general equation for the intensity rate equation and can be used according to our needs. For example, for the investigation of the output spectrum when the effect of saturation is not included in the intensity rate equation, we may let μ = 0. In this case for the H-broadening from Eq. (31) we have,

To obtain Eq. (32) we have also used 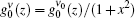
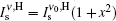
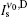

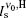
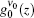

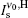
For the calculation of the ASE intensity at the resonance transition of ν = ν 0, we let x = 0, and consequently Iν 0(z) is calculated. When the effect of saturation is not considered, μ in the intensity rate equation is equal to zero, whereas by including the saturation effect, μ is equal to 1 or 1/2. For the numerical calculation, it is necessary to use the z-dependency of γ (z). As we deal with a small-sized sample having a width of dAMP and a thickness s, we use γ (z) = sdAMP/4 π z2 throughout the calculation. Here, we examine the H- and D-broadenings, both, and consequently we solve the equations with μ = 0, μ = 1, and μ = 1/2 conditions. As both solutions for the cases of using (μ = 0, 1) or (μ = 0, 1/2) explain one set of experimental data points, the corresponding solutions for each case must be overlapped with different gain-parameters. The intensity profiles corresponding to the numerical solutions start at a threshold length zth, and increase along the z direction. The results corresponding to the numerical and analytical approaches are given in Section 4, and the corresponding parameters for the H-broadened system appearing in the relevant calculated graphs are also summarized in Table 1.
| Table 1. Deduced gain parameters and threshold lengths and gain coefficients for lAMP = 0.2 cm. |
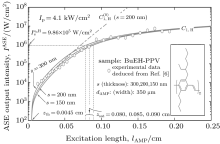
 | Fig. 2. Plots of the ASE calculation with μ = 0 (dashed line), and μ = 1 (solid line), showing the effect of the saturation effect in the intensity rate equation. The C1, H-profile is borrowed from Fig. 1, and compared with the C0-profile. The inset shows the analysis when equation (1) is used for fitting to the linear part of the measurement in a logarithmic scale. Measurements are given in Ref. [6]. |
To observe the validity of the GDGC model, we use the experimental measurements for planar wave guides of BuEH-PPV reported by McGehee et al.[6] For the calculation, initially, the following parameters are used: λ 0 = 562 nm, s = 200 nm, and dAMP = 350 μ m (s is the thickness and dAMP is the width of the target). n = 1.76 is the sample index of refraction. Δ λ 0 = 47 nm is the measured spontaneous emission bandwidth. In Ref. [6], the experimental measurements of IASE versus excitation length are given with four different pumping intensities of Ip = 0.61, 1.2, 2.2, 4.1 kW/cm2. The measured ASE bandwidths are also given by plots of Δ λ ASE versus excitation length for Ip = 0.61 kW/cm2 and 4.1 kW/cm2. The gain parameters 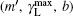
The fluorescence quantum yield of 0.62 is given in Ref. [6], then it must be identified with one of the IASE versus lAMP experimental plots it belongs to. With the upper state lifetime τ u, nonradiative lifetime τ nr, and 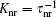
For the input pump intensity of Ip = 4.1 kW/cm2 and ϕ = 0.62, the calculated output intensity at ν = ν 0 is given in Fig. 1. In this calculation 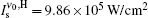
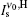
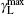
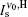



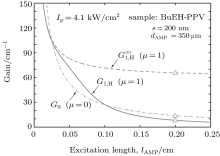 | Fig. 3. The saturated G1, H and G0 gain profiles for the μ = 1, and μ = 0 calculations, according to the deduced gain parameters given in Table 1. The  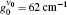 |
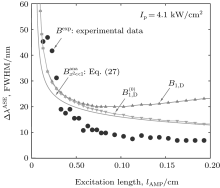
The calculated bandwidths for Ip = 4.1 kW/cm2 are shown in Figs. 4(a) and 4(b). In Fig. 4(a), in addition to the numerical calculations, the experimental measurements of (Δ λ )ASE, shown by the Bexp-profile are also introduced. According to three different views for the previously introduced calculations of the saturated and unsaturated intensity profiles, here three different views for the calculated bandwidths are also given. They are shown by the B0, B1, H, and 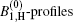
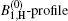

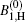
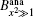

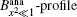
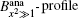
 | Fig. 4. (a) Plots of the calculated ASE bandwidth versus the excitation length. The B0-profile corresponds to the μ = 0 solution. The B1, H-profile for μ = 1, and the 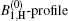  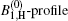 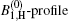  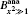 |
The numerical calculations for the ASE output intensity versus x for large and also short distances (for example z = 0.203 cm and z = 0.013 cm, respectively) are carried out and the results are given in Figs. 5(a) and 5(b), respectively. For identifying the calculated intensity distribution, a Gaussian and a Lorentzian function of the type
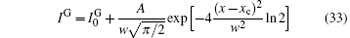
and
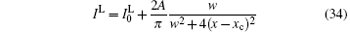
are fitted to the numerically calculated profiles, and the parameters 
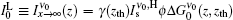

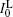
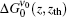
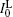

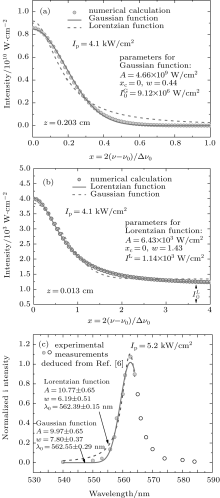 | Fig. 5. Plots of the calculated ASE intensity versus normalized frequency offset x = 2(ν − ν 0)/Δ ν 0 (a) for z = 0.203 cm, showing that the calculated intensity favors a Gaussian distribution and verifies the x2 ≪ 1 approximation for the intensity; (b) for z = 0.013 cm, showing that the calculated intensity has a Lorentzian distribution and that corresponds to the x2 ≫ 1 approximation. Both panels (a) and (b) correspond to Ip = 4.1 kW/cm2; (c) the plots of normalized ASE intensity versus wavelength for Ip = 5.2 kW/cm2 measurements as given in Ref. [6]. The experimental measurements show that IASE at high pump intensity, when z ≫ zsat is satisfied, favors a Gaussian frequency distribution. |
For Ip = 0.61 kW/cm2, in addition to the reported ASE intensity and bandwidth versus excitation length measurements, a plot of the normalized measured intensity versus wavelength is also given in Fig. 6. For the 0– 0 vibrational transition when two different types of functions: Gaussian and Lorentzian are fitted to the leading portion of the spectrum, as seen in the figure, the distribution favors a Lorentzian function at this low incident intensity. Thus, for this experimental condition, at the exit face of the target, we have enough confidence that the condition of z ≪ zsat is satisfied and consequently the intensity distribution keeps homogeneously broadening throughout the excitation length. For the further verification of the model, the calculation is performed numerically for the ASE and bandwidth reduction according to the measurements reported in Ref. [6]. In Fig. 7, the calculated IASE versus the excitation length for μ = 0 and μ = 1 solutions are given. The overlapped profiles in this figure show that at the low value of the input pump intensity Ip, the condition of 


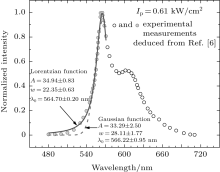 | Fig. 6. Normalized experimental measurements of IASE versus wavelength for Ip = 0.61 kW/cm2 reported in Ref. [6]. The fittings to a Gaussian function and a Lorentzian function show that the intensity distribution favors a Lorentzian function at low input intensity. |
 | Fig. 7. Calculated ASE intensity corresponding to Ip = 0.61 kW/cm2 input intensity for μ = 0 and μ = 1 solutions shown by the C0, C1, H, and  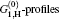   |
 | Fig. 8. Plots of the calculated ASE bandwidth, shown by the overlapped profiles of B0, B1, H, and 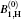 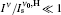 |
For observing that at a low Ip-value the Lorentzian distribution function maintains a Lorentzian frequency distribution along the whole excitation length of the sample, the ASE intensities for the excitation lengths of z = 0.20 cm and z = 0.01 cm are numerically calculated and the results are shown in Fig. 9. Again, fittings of a Lorentzian function and a Gaussian function to the calculated intensity profiles show that in both cases the frequency distributions favor a Lorentzian function. Thus, it is shown that by different approaches of using experimental measurements, as indicated in Ref. [6] and numerical calculations, a homogeneously broadened transition is involved in the light– matter interaction for the BuEH-PPV sample at different pump intensities. Figures 6 and 5(c) show that by increasing Ip from Ip = 0.61 kW/cm2 to 5.2 kW/cm2, the peak of the IASE shifts from 564.70 nm to 562.55 nm, i.e., it is blue-shifted. This behavior has also been shown by experimental graphs in slab organic crystals in the study of two-photon pumped ASE.[27] Here, regardless of the frequency shift, the effect of the pump intensity on the intensity behavior on switching from the Lorentzian distribution to the Gaussian distribution when the pump intensity increases is also explained by the proposed approach.
In order to complete our analysis on the BuEH-PPV sample, the numerical calculations are also carried out on the assumption that the line is inhomogeneously broadened. In this case, the calculation results of bandwidth and gain coefficient have not explained the experimental measurements correctly.
To observe the results corresponding to the D-broadening, in Fig. 10 the ASE intensity versus lAMP is depicted. C1, D and 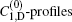
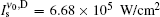

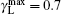
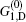
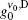
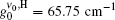

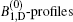
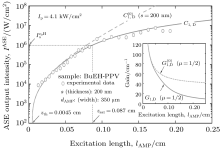 | Fig. 10. Plots of the calculated ASE intensity for D-broadened line-shape for saturated C1, D- and unsaturated 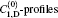 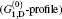 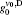 |
According to the measurements appearing in Ref. [6] and the introduced model for data analysis, as given here, we calculate the gain parameters, unsaturated and saturated gain coefficients for Ip = 4.1, 2.2, 1.2, 0.61 kW/cm2. By referring to Fig. 12, in addition to introducing the plot of the unsaturated gain coefficient 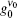
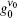



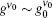
 | Fig. 12. Behaviors of the m′ deduced parameter and gain coefficient versus input intensity Ip. Gain parameter 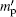 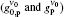 |
By using Fig. 12, if we let
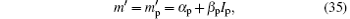
where α p and β p are constants, then equation (3) shows that for 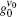
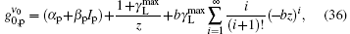
where z = lAMP = 0.2 cm, i.e., the total excitation length is used for this analysis. 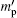
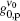


then, we observe that equation (36) is simplified into
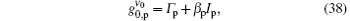
which is true for the present analysis, as according to Table 1, 
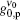
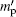
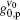
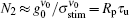

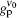
In this work, the ASE in a planar waveguide BuEH-PPV sample of 2 mm in length, pumped by a laser pulse of 0.34 kW/cm2 to 5.2 kW/cm2, is investigated. For this purpose a model of geometrically dependent gain coefficient and the intensity rate equation are used to explain the ASE intensity behavior and bandwidth reduction for the pumped sample. It is shown that the system is homogeneously broadened with a Lorentzian frequency distribution, which at high input intensity switches smoothly to a Gaussian frequency distribution. That is, when the z ≫ zsat condition is satisfied, the distribution is a pure Gaussian function. At the low input intensity, on the other hand, the distribution behaves as a Lorentzian frequency function, because the experimental conditions have not reached the saturation. This corresponds to the z ≪ zsat condition. By analyzing the measured ASE intensity and bandwidth, the unsaturated 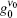

| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|