It is known that gallium oxide (Ga₂O₃) is an important wide band gap semiconducting material with good chemical and thermal stability. Ga₂O₃ can crystallize into different polymorphic phases such as rhombohedral α -, monoclinic β -, cubic γ - (spinel), and δ -Ga₂O₃ phases.^[1] Among them, the monoclinic β -Ga₂O₃ is known to be the most stable form at ambient conditions. It undergoes phase transition from β -Ga₂O₃ to α -Ga₂O₃ upon increasing pressure.^{[2, 3]} The α - and β -Ga₂O₃ has a wide band gap of above 4  eV, which enables it to modify their properties such as transportation, photoluminescence, as well as magnetism by the incorporation of suitable ions in the Ga₂O₃ lattice.^{[4– 9]} For the β -Ga₂O₃, the Ga³⁺ ions are accommodated in non-equivalent tetrahedral and octahedral sites, preferential substitution for Ga³⁺ ions on either the tetrahedral or the octahedral sites depending on the radius of the impurity ions has been frequently observed. Consequently, the influence of the impurities on the properties of β -Ga₂O₃ could be complex.^{[5, 7, 10]} In the α -Ga₂O₃, all the cations reside on the octahedral sites, and it is isostructural with the well-known hematite with a well established high ferromagnetic transition temperature of ∼ 670  K.^[11] Thus, Fe³⁺ ions would be desirable to manipulate the magnetic properties of α -Ga₂O₃ for the practical application.

Experimental results of α -Ga_{2− x}Fe_xO₃ series are encouraging to achieve the non-conventional ferromagnetic semiconductor for room-temperature spintronic applications, including band gap tailoring, photoconductivity, ferromagnetism, multiferroic domain switching, and ferroelectric polarization.^{[12– 17]} However, most of previous work has been focused on the properties of α -Ga_{2− x}Fe_xO₃ with an Fe content x higher than 0.5. Kaneko et al. reported the preparation of high crystalline α -Ga_{2− x}Fe_xO₃ thin films (0 ≤ x ≤ 2) by mist chemical vapor deposition, and revealed that ferromagnetism occurred at a temperature of ∼ 110  K when x∼ 0.5.^{[4, 18]} Amores et al.^[19] reported the synthesis of a solid solution of α -Ga_{2− x}Fe_xO₃ with 0 ≤ x ≤ 2 at ambient pressure, and the obtained α phase was shown to be stable only below 400  ° C. However, the solid solution is a mixture of α and β phases when the Fe content is low. The compression experiments showed that the transition of β → α occurred at a pressure as high as 20– 22  GPa at room temperature.^[20] However, it has been shown that the pressure required for the stabilization of the metastable α -Ga₂O₃ can be greatly reduced at elevated temperatures.^[21] So far, there are scare reports on the high-pressure synthesis and properties of Fe³⁺ -doped α -Ga₂O₃ with the doping level less than 0.5. In the present study, a single phase of Fe³⁺ -doped α -Ga_{2− x}Fe_xO₃ with x ≤ 0.4 is fabricated at high temperature and high pressure to explore the effect of Fe³⁺ doping on the structural, magnetic, and optical properties of α -Ga₂O₃.

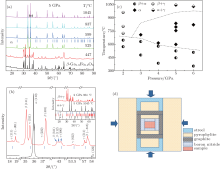
In  order  to  synthesize  the  Fe³⁺ -doped α -Ga₂O₃, i.e., α -Ga_{2− x}Fe_xO₃ (x ≤ 0.4) (refer to α -GF_xO thereafter), we firstly synthesized the Fe³⁺ -doped β -Ga₂O₃, i.e., β -Ga_{2− x}Fe_xO₃ (x ≤ 0.4) (refer to β -GF_xO thereafter) as a starting material. The details of the preparation of β -GF_xO with x = 0.1, 0.2, 0.3, and 0.4 can be found elsewhere.^[22] Briefly, the starting powders of β -Ga₂O₃ (99.999%, − 325 mesh, Alfa Aesar) and α -Fe₂O₃ (99.99%, − 325 mesh, Alfa Aesar) were mixed in the designed atomic ratio of Ga to Fe by a vario-planetary ball miller (Pulverisette 4, Fritsch, Germany) at a rotation speed of 200  RPM for 10  hours. After the milling, the obtained mixtures were dried at 90  ° C for 24  hours and subsequently pressed into a pellet of 10  mm in diameter. A single phase of β -GF_xO (x = 0.1, 0.2, 0.3, 0.4) was then obtained after sintering in air at 1350  ° C for 10  hours. The α -GF_xO (x = 0.0, 0.1, 0.2, 0.3, 0.4) managed to synthesize with the precursors of the as-received β -Ga₂O₃ and as-prepared bulk samples of β -GF_xO (x = 0.1, 0.2, 0.3, 0.4) in a single large-volume cubic anvil press under high pressure and high temperature. The precursors were inserted into the graphite furnace with a pure h-BN layer, which served as a barrier, as shown by the sample assembly in Fig.  1(d). The sample assembly was sintered under compressive pressures of 2– 6  GPa and temperatures of 350– 1050  ° C for one hour, and then allowed to cool rapidly to room temperature.

Fig.  1.

Figure Option ViewDownloadNew Window

Fig.  1. (a) Powder XRD patterns for the starting β -Ga1.8Fe0.2O3 sintered under a compressive pressure of 5  GPa and at different temperatures. The bars are the Bragg position of α -Ga2O3 (PDF# 06-0503). (b) Enlarged powder XRD patterns for the β -Ga1.8Fe0.2O3 sintered at 2  GPa and 961  ° C (upper, red), 5  GPa and 1045  ° C (lower, black), and the inset shows the full scale of these patterns. The bars correspond to the Bragg positions of α -, β -, and spinel γ -structure with the PDF#s of 06-0503, 41-1103, and 20-0426 respectively. (c) Temperature and pressure diagram for the sintering of β -Ga1.8Fe0.2O3. The dashed lines guide the eye. (d) An illustration of the sample assembly for the treatment at high temperature and high pressure.

The as-sintered samples were carefully polished to remove any possible contamination from the barrier, and then ground for the structure characterization, which was performed by powder X-ray diffraction (XRD) with Cu K_α radiation (PC/Dmax 2500, Rigaku, Japan). The XRD spectra were analyzed via the Rietveld refinements using software package of FullProf Suite (v2.05).^[23] The Calorimetric measurements were conducted on the ground powder by a simultaneous thermal analyzer (STA  449C  Jupiter, Netzsch, Germany) with a heating rate of 10  ° C· min^{− 1} under the atmosphere of high-purity air. The magnetic measurements were carried out using a vibrating sample magnetometer attached to the PPMS (Quantum Design, USA). The diffuse reflectance was measured using a UV– Vis spectrophotometer equipped with an integrating sphere (UV-2550, Shimadzu, Japan). The reference sample is barium sulfate (Wako 1^st grade, Wako Pure Chemical Industries, Ltd., Japan).

In order to elucidate the required pressure and temperature for the preparation of single phase of Fe³⁺ -doped α -Ga₂O₃ from the starting powder of Fe³⁺ -doped β -Ga₂O₃, a concentration of 10  at% Fe³⁺ was chosen (i.e., β -Ga_1.8Fe_0.2O₃ or β -GF_0.2O) and treated at different temperatures and pressures. Figure  1(a) shows the collected powder XRD spectra at room temperature for the sintered β -GF_0.2O under a compressive pressure of 5  GPa with different temperatures. With the increase in temperature, diffraction lines of β -GF_0.2O (PDF# 41-1103) were observed to decrease in intensity and broaden in width, disappeared at ∼ 599  ° C. Bragg peaks of α -GF_0.2O (PDF# 06-0503) were observed to appear at ∼ 447  ° C and increases in intensity upon increasing temperatures. The β -GF_0.2O was completely transformed to α -GF_0.2O at a temperature higher than 599  ° C. The observed transition of β → α at elevated temperatures is in good agreement with previous reports.^[21] However, we find that the temperature required for the synthesis of single phase of α -GF_0.2O is as low as ∼ 600  ° C, which is quite low in comparison with that reported in Ref.  [21]. A new set of diffraction peaks appears beside those of the α -GF_0.2O (Fig.  1(c)) when the temperature is increased to 1045  ° C, which is close to the limitation of the safety temperature of our apparatus. These peaks coincide well with the diffraction lines of spinel-type γ -Ga₂O₃ (PDF# 20-0426), except for a downshift of the diffraction lines due to the larger radius of Fe³⁺ . Various pressures and temperatures were tried to treat the starting powder of β -GF_0.2O, and the XRD data of these samples were analyzed and summarized in Fig.  1(b). It demonstrates that the temperature window for the synthesis of single α -phase is narrowed down when decreasing the sintering pressure. By decreasing the pressure to 2  GPa, there is no single phase of α -GF_0.2O observed, and the as-prepared sample shows a mixture of either β + α or β + γ .

According to the temperature– pressure (T– P) phase diagram shown in Fig.  1(b), the sintering pressure and temperature are chosen to be 5  GPa and 850  ° C, respectively, for the synthesis of single phase of α -GF_xO with x = 0, 0.1, 0.2, 0.3, and 0.4. Figure  2(a) shows the collected powder XRD spectra at room temperature for the sintered α -GF_xO samples, confirming the single phase of corundum-type structure of undoped and Fe³⁺ -doped samples. The enlarged diffraction peaks of (110) in the inset of Fig.  2(b) display clearly that the diffraction peaks shift consistently towards the lower angle with the increase of Fe³⁺ content, demonstrating the expansion of lattice constants induced by the successful replacement of Ga³⁺ by Fe³⁺ . The Rietveld refinements with consideration of the corundum R-3c symmetry were carried out on the XRD spectra of the Fe³⁺ -doped and undoped α -Ga₂O₃. As a typical example, the experimental and calculated XRD spectra for α -GF_0.2O are shown in Fig.  2(b). For all the synthesized samples, the calculated spectra are in a good agreement with the experimental ones, with the agreement factors of the weighted profile factor and the goodness of fitting larger than 10 and 6, respectively. For the as-prepared α -Ga₂O₃, the lattice parameters a and c, and the unit cell volume are determined to be 4.9814(5)  Å , 13.4327(3)  Å , and 288.671(3)  Å ³, respectively, which are consistent with previous report.^[21] The lattice constants of a and c, and the unit cell volume increase upon increasing the Fe³⁺ content (Fig.  2(c)), demonstrating the doping-induced structural expansion along the different axes.

Fig.  2.

Figure Option ViewDownloadNew Window

Fig.  2. (a) Powder XRD patterns for α -Ga2− xFexO3 with x = 0, 0.1, 0.2, 0.3, and 0.4 synthesized at 5  GPa and temperature of 800  ° C for 1  hour. (b) A typical Rietveld refinement for the as-prepared α -Ga1.8Fe0.2O3. Empty circles represent the experimental data, and solid line is the calculated one. The curve at the bottom is the difference between the experimental and calculated data, and the vertical lines represent the Bragg positions of α -Ga2− xFexO3 and standard silicon. Inset shows the enlarged (104) Bragg peak of α -Ga2− xFexO3, showing the systematic shift towards the lower angle upon increasing the Fe3+ content. (c) Refined lattice parameters (a, c, and unit cell volume) as a function of the Fe3+ content for α -Ga2− xFexO3.

To investigate the thermostability of sintered α -GF_xO, we employ a differential scanning calorimetry (DSC) for samples of α -GF_xO (x = 0, 0.1, 0.2, 0.3, 0.4) in the temperature range from room temperature to 1100  ° C. No appreciable changes of the thermogravimetry (TG) signals are found over the entire temperature range for investigated samples. For the undoped and Fe³⁺ -doped α -Ga₂O₃ samples, there is only one exothermic peak observable from room temperature to 1100  ° C. The exothermic peak was observed to occur at an onset and peak temperature of ∼ 560  ° C and ∼ 594  ° C respectively for the undoped α -Ga₂O₃, and they were found to shift toward higher temperature with the increase of Fe³⁺ content (Fig.  3(c)). After one thermo-cycle, XRD results show that the final product is single phase of β -GF_xO with a monoclinic structure (Fig.  3(c)). Thus, the exothermic peaks are attributed to the transition of the metastable α -GF_xO to the stable β -GF_xO. The area of the exothermic peak, which corresponds to the enthalpy change Δ H associated with the transition of α -GF_xO→ β -GF_xO, is determined to be ∼ – 3.7  kJ· mol^{- 1} for the undoped α -Ga₂O₃, being in a reasonable agreement with the theoretical expectation at 5  GPa.^[24] It decreases with the increase of Fe³⁺ content (Fig.  3(b)), being indicative of the decreased energy difference between the Helmholtz free energy of β -phase and α -phase, which is consistent with the theoretical expectation.^[24]

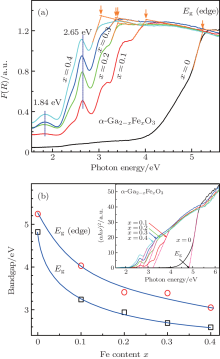
The doping of Fe atoms into the Ga sites of α -Ga₂O₃ structure is further confirmed from the absorption spectra of the samples in UV– Visible range (200– 1000  nm). The required relative diffuse reflectance spectra R refering to the BaSO₄ standard of the undoped α -Ga₂O₃ and Fe³⁺ -doped α -GF_xO samples were converted to the Kubelka– Munk functions F(R) (= (1 − R)²/2R) and shown in Fig.  4(a), where F(R) is proportional to the absorption coefficient.^[25] For the undoped α -Ga₂O₃ sample, a strong absorption edge is observed to occur at E_g (edge) ∼ 5.3  eV. With the increase of Fe³⁺ concentration, the absorption edge shifts systematically toward lower energy (Fig.  4(b)). For the Fe³⁺ -doped α -GF_xO, a number of subspectra are observed below the absorption edge, which is consistent with the previous report.^[19] In the octahedral environment of Fe³⁺ ions (i.e., FeO₆) five-fold degeneracy of d orbital splits into low-energy t_2g and higher-energy e_g levels. Transition of electrons between these levels contributes to absorption bands in the UV– Vis region. Among these subspectra, the bands at ∼ 1.8  eV and ∼ 2.6  eV are well defined and found to shift toward a lower energy with the increase of Fe³⁺ content. They are ascribed to the electronic transitions of ⁶A_1g (⁶S) → ⁴T_2g(⁴G) and ⁶A₁(⁶S) → ⁴T_2g(⁴D) of Fe³⁺ respectively, according to previous work on oxides containing Fe³⁺ and Mn^{2 +} (3d⁵).^{[26, 27, 28]}

Fig.  3.

Figure Option ViewDownloadNew Window

Fig.  3. (a) The DSC signals at the temperatures near the exothermic peak for powder samples of α -Ga2− xFexO3 with x = 0, 0.1, 0.2, 0.3, and 0.4 synthesized at 5  GPa and temperature of 800  ° C for 1 hour. The curves are shifted on the Y axis for a better view. (b) The peak temperature and integral area (associated enthalpy change Δ H) of the exothermic peak as a function of Fe content. (c) The powder XRD patterns of the products after one thermal cycle of α -Ga2− xFexO3 (x = 0, 0.1, 0.2, 0.3, 0.4). The bars show the Bragg position of β -Ga2O3 (PDF# 41-1103).

Fig.  4.

Figure Option ViewDownloadNew Window

Fig.  4. Diffuse reflectance spectra of α -Ga2− xFexO3 with x = 0, 0.1, 0.2, 0.3, and 0.4. (a) The Kubelka– Munk function F(R), which is proportional to the absorption coefficient, converts from the relative diffuse reflectance spectra R. The downside arrows denote definition of the bandgap at the absorption edge Eg (edge). The vertical lines show the position of two absorption peaks corresponding to the d-d transition of octahedrally coordinated Fe3+ ions. (b) Optical bandgap Eg and Eg (edge) as a function of Fe3+ content. Inset is the Tauc plot of (F(R)× hν )2 versus hν showing the definition of the Eg. The solid lines guide the eyes.

In order to determine the room-temperature optical bandgap (E_g) of the undoped α -Ga₂O₃ and Fe³⁺ -doped α -Ga_{2− x}Fe_xO₃ samples, we use the relational expression proposed by Tauc et al.^[29] in conjunction with the Kubelka– Munk function for a semiconductor, hν F(R) ∝ A(hν − E_g)^{m / 2}, where h is the Planck constant, hν the incident photon energy, m is related to the nature of transition and is 1 or 4 for a direct or indirect allowed transition, and A the proportional constant independent of the photon energy. For the pure α -Ga₂O₃ and α -Fe₂O₃, or Ga-doped Fe₂O₃, it was reported that the band gaps are of direct transition, ^{[12, 30, 31]} and we take the assumption of direct transition for the Fe³⁺ -doped α -Ga₂O₃. Therefore, the energy intercept of Tauc plot^[32] of (F(R)× hν )² versus hν gives E_g for a direct allowed transition when the linear region is extrapolated to zero ordinate, as indicated in the inset of Fig.  4(b). The determined E_g for the undoped α -Ga₂O₃ is ∼ 5.3  eV, being consistent with the published values of 4.9– 5.6  eV.^{[9, 30, 31, 33]} Upon increasing the Fe³⁺ concentration, E_g is found to decrease monotonically (Fig.  4(b)), reaching a value of ∼ 2.9  eV of the sample with the Fe³⁺ concentration x = 0.4. The decrease of optical energy gap and red shift of absorption band indirectly confirm the doping of Fe into α -Ga₂O₃ structure.

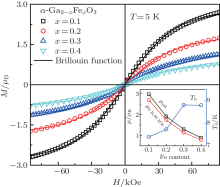
Figures  5(a)– 5(d) show the DC magnetization M versus magnetic field H curves measured at different temperatures for α -GF_xO with x = 0.1, 0.2, 0.3, and 0.4, respectively. For the sample of α -GF_0.1O, no magnetic hysteresis is detectable (inset of Fig.  5(a)). It does not behave in a paramagnetic way at low temperature since the plot of M as a function of the ratio of H to T does not comply with the Langevin theory of paramagnetism. When the Fe³⁺ concentration x is increased to 0.2 or higher, remnant magnetization is observed (inset of Figs.  5(b)– 5(d)). The slanted hysteresis diagrams of the remnant fields versus applied field are similar to ferromagnetic diagrams. However, for all the samples with the Fe³⁺ content higher than 0.2, the coercive field of ∼ 10  mT and the remanence on an order of ∼ 10^{− 3}μ _B per Fe³⁺ ion are obtained. The hysteresis loop is reduced with increasing temperature and vanishes at ∼ 30  K. Such a small magnetic moment, however, cannot be explained as a simple ferromagnetic ordering of localized spins but a frozen ferromagnetic moment in the spin-glass state.

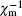
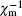
The inset of Fig.  6 is the inverse susceptibility of as a function of temperature for samples of α -GF_xO. In the high temperature range, displays the linear variation with temperature in the range of 150– 300  K, following the Curie– Weiss law. Moreover, the extrapolation of the fitting lines show positive intercepts, demonstrating an antiferromagnetic coupling between the Fe³⁺ ions in α -Ga_{2− x}Fe_xO₃.

In order to investigate the antiferromagnetic coupling in the diluted magnetic semiconductors, a modified Brillouin function is used to describe the magnetization behavior by introducing the effective temperature (T_eff) and the effective saturation magnetization (μ _sat) per magnetic ion or the effective concentration (x_eff) of magnetic ions.^{[34, 35]} For the Fe³⁺ -doped α -GF_xO, the modified Brillouin function.^[34]M = (xN_Aμ _sat/m_x) B_5/2(5/2gμ _BH/k_BT_eff) is used to fit the measured M versus H curves at 5  K for α -GF_xO, where g = 2, μ _B is the Bohr magneton, N_A and k_B are Avogadro and Boltzman constants, respectively, x is the Fe³⁺ concentration, and m_x is the molar mass of α -GF_xO. T_eff = T+ T₀ and μ _sat are used as the fitting parameters, which can be used to reflect the antiferromagnetic superexchange interaction between the Fe³⁺ ions.^[35] Figure  7 shows that the fitting is in good agreement with the measured M versus H curves at 5  K for α -GF_xO, and the, inset, shows, the, obtained, T₀, and μ _sat as a function of the Fe³⁺ content x. In the sublattice of α -GF_xO, if two Fe³⁺ ions via an intermediate oxygen ion forms an antiferromagnetic pair of Fe³⁺ – O– Fe³⁺ , their moments can be cancelled and make no contribution to the measured magnetization. Only the uncoupled Fe³⁺ ions can be aligned in the applied magnetic field, according to the Brillouin function with T_eff greater than the real temperature T or positive T₀. Thus, the obtained value of μ _sat smaller than 5.92μ _B and the positive T₀ indicate that a fraction of Fe³⁺ ions form the Fe³⁺ – O– Fe³⁺ pairs with antiferromagnetic superexchange interaction. At 5  K, the saturation cannot be obtained at the magnetic field of 85  kOe. Thus, the measured magnetic moment per Fe³⁺ ion at 5  K and 85  kOe is smaller than the effective saturation moment μ _sat obtained from the fitting, but they show similar dependence on the Fe³⁺ content x. With the increase of the Fe³⁺ content x, the decrease of μ _sat is suggestive of the formation of more Fe³⁺ – O– Fe³⁺ pairs with the antiferromagnetic superexchange interaction. Moreover, T₀ is found to increase with the increase of Fe³⁺ content x. These behaviors of the obtained μ _sat and T₀ indicate that the antiferromagnetic interaction between the magnetic ions becomes stronger with the increase of the Fe³⁺ content.^[35]

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. (a) Magnetization as a function of the magnetic field for the sample α -Ga2− xFexO3 at different temperatures. (a) α -GF0.1O at 5, 20, and 100  K. (b) α -GF0.2O at 5, 10, 20, 50, and 100  K. (c) α -GF0.3O at 5, 10, 30, 50, and 100  K. (d) α -GF0.4O at 5, 10, 20, 50, 80, and 100  K. Inset is the enlarged plots of M– H loops of the corresponded temperatures.

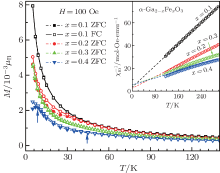
Figure  6 shows the temperature dependence of zero-field cooling (ZFC) and field cooling (FC) of the DC magnetization measured in the magnetic field of 100  Oe for α -GF_xO with x = 0.1, 0.2, 0.3, and 0.4. For the sample of α -GaF_0.1O, the ZFC curve coincides with the ZFC curve. Irreversible magnetization (splitting of ZFC and FC magnetization) is observed to occur at the temperature of ∼ 33  K for x = 0.2 and shifts slightly towards higher temperature with the increase of Fe³⁺ content, and at ∼ 42  K when x = 0.4. This is consistent with the previous reports that the spin freezing temperature increases with the increased concentration magnetic ions.^[36] In addition, for the sample of GF_0.4O, a second splitting of ZFC and FC magnetization is observed to occur at a lower temperature of ∼ 7.2  K.

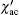
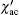
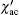
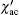
Temperature-dependent AC susceptibility is measured to investigate the dynamics of the magnetization of the spontaneous magnetic behaviors of the Fe³⁺ -doped α -GF_xO. Figure  7 shows the real part and imaginary part of AC susceptibility χ _ac measured at the temperatures of 5– 300  K and frequencies of 0.5, 0.9, 1.0, 5, and 7  kHz for α -GF_xO (x = 0.1, 0.2, 0.3, 0.4). The real part at 5  K decreases in amplitude with the increase of Fe³⁺ content (top panels of Figs.  8(a)– 8(d)). Small shoulders of could be distinguished at the temperature when the maxima of occurs, and show very weak frequency dependence. For sample GF_0.1O, noticeable anomalies of are observed to occur at a temperature of ∼ 33  K when the frequency is higher than 1  kHz (Fig.  8(a)), though no evident splitting of the ZFC and FC magnetization is observed. As the Fe³⁺ content increases to x = 0.2, as shown in the inset of bottom panel of Fig.  8(b) for sample GF_0.2O, noticeable anomalies occur in at ∼ 30  K, which is close to the spin freezing temperature of the sample α -GF_0.2O (Fig.  6). The anomaly in shows a clear frequency dependence in amplitude and a very weak frequency dependence in temperature, which can be attributed to the entrance of spin glass.^{[37– 39]} With the increase of Fe³⁺ content, the anomaly in measured at 7  kHz is found to decrease in amplitude and shift toward higher temperatures. For the sample GF_0.3O, the curves of at all the frequencies turn to increase rapidly at ∼ 8  K with the decrease of temperature (bottom panel of Fig.  8(c)), and presumably the maxima of occur at a temperature below 5  K. This is more evident for the sample GF_0.4O (bottom panel of Fig.  8(d)), clear anomalies of and are observed to occur at a lower temperature of ∼ 7.2  K, where the splitting of ZFC and FC magnetization is also observed to occur (Fig.  6). In addition, the anomaly increases in amplitude and shifts slightly to higher temperatures with the increase of frequency. The occurrence of two distinct peaks in as well as two spin freezing temperatures observed in the DC magnetization of GF_0.4O indicate the existence of two distinct spin glass states as suggested^{[40– 43]} and also confirm the two phase transition temperatures at ∼ 7.2  K and 40  K.

Fig.  6.

Figure Option ViewDownloadNew Window

Fig.  6. Zero-field cooling (ZFC, solid symbols) and field cooling (FC, empty symbols) of the DC magnetization as a function of temperature from 5 to 140  K for α -Ga2− xFexO3 with x = 0.1, 0.2, 0.3, and 0.4. A magnetic field of 100  Oe is applied for all the measurements. Arrows denote the definition of the temperatures where irreversible magnetization occurs. Inset is the inverse molar susceptibility as a function of temperature for α -Ga2− xFexO3 with x = 0.1, 0.2, 0.3, and 0.4. The dash lines are the linear fitting.

Fig.  7.

	Figure Option ViewDownloadNew Window
	Fig.  7. Magnetization as a function of the magnetic field measured at 5  K for α -Ga2− xFexO3 with x = 0.1, 0.2, 0.3, and 0.4. Solid lines are the fittings to the modified Brillouin function. Inset is the measured magnetic moment per Fe3+ ion at 85  kOe and 5  K, the calculated saturation magnetic moment per Fe3+ ion, and the temperature T0 as a function of the Fe3+ content.

According to previous work on the anisotropic spin-glasses, .^{[42, 44– 46]} the above-mentioned two spin-glasses transitions observed from paramagnetic state could occur in the presence of random exchange interaction and local uniaxial magnetic anisotropy. On one hand, the α -Ga₂O₃ is isostructrual with α -Fe₂O₃, and Ga³⁺ ions can be unlimitedly substituted by Fe³⁺ ions with very limited distortion to the crystal structure due to the small difference of the radius of Ga³⁺ ion and Fe³⁺ ion. In α -Fe₂O₃, it is well known that there are two magnetic sublattices with equal moment that interact via an antiferromagnetic coupling, and a small canting of the two sublattices results in weak ferromagnetism between the Morin temperature and the Né el temperature.^{[47, 48]} Thus, it is believed that the incorporated Fe³⁺ ions on two sublattices are diluted by the nonmagnetic Ga³⁺ ions and are randomly distributed over the corresponding sublattices. Although they are randomly coupled through the AFM superexchange interactions, these bonds do not make up a periodic structure, and long-range AFM order cannot set in among the moments located in the two sublattices. On the other hand, it was suggested that the easy axis of magnetic anisotropy arises from the magnetic dipole anisotropy and single-ion anisotropy changes during the spin reorientation at the Morin temperature.^[47] Such an anisotropy also existed and resulted in a large coercivity in Fe-doped α -Ga₂O₃.^[13] It is shown here that the temperatures associated with spin temperature increase with the increase of Fe³⁺ ion concentration. We believe that two spin-glasses behavior could occur and be more profound in α -GF_xO with the Fe³⁺ concentration x higher than 0.4, though ferromagnetic ordering was reported to form at x ≈ 0.5.^{[4, 18]} A detailed investigation of the spin dynamics in the Fe³⁺ -doped α -Ga₂O₃ (0.4 ≤ x ≤ 0.6) will be discussed.

Fig.  8.

Figure Option ViewDownloadNew Window

Fig.  8. The AC susceptibility χ ac measured in a zero dc magnetic field as a function of temperature at the frequencies of 0.5, 0.9, 1, 5, and 7  kHz for α -Ga2− xFexO3 with (a) x = 0.1, (b) 0.2, (b) 0.3, and (d) 0.4. The top and bottom panel of each figure correspond to the real () and imaginary (χ ac) parts of χ ac. The AC driving magnetic field has an amplitude of 5  Oe. Insets of the bottom panel show χ ac in low temperature range, and arrows show the peak temperature of the corresponding samples.

In summary, a series of single-phase Fe³⁺ -doped wide gap oxide of α -Ga₂O₃, i.e., α -Ga_{2− x}Fe_xO₃ with x = 0.1, 0.2, 0.3, and 0.4, has been successfully fabricated via treating single phase of β -Ga_{2− x}Fe_xO₃ at high temperature and high pressure. Rietveld refinements of the X-ray diffraction data show that the lattice constants increase monotonically with the increase of Fe³⁺ content. Calorimetric measurements show that the temperature of the phase transition from α -GF_xO to β -GF_xO increases, while the associated enthalpy change decreases upon increasing Fe³⁺ content. The optical energy gap deduced from the reflectance measurement and the absorption edge are found to decrease monotonically with the increase of Fe³⁺ content. Below the E_g edge, optical absorption structures are observed to occur at ∼ 1.8 and ∼ 2.6  eV, which are attributed to the d– d transitions of the crystal-field splitting of 3d⁵ multiplets of the octahedrally coordinated Fe³⁺ ion. From the analyses of the magnetic measurements, it is found that a fraction of the doped Fe³⁺ ions form the Fe³⁺ – O– Fe³⁺ pairs with antiferromagnetic superexchange interaction. The Fe³⁺ – O– Fe³⁺ pairs should increase in number with the increase of Fe³⁺ content, leading to the observed reduction in the measured magnetic moment per Fe³⁺ ion. The two distinct anomalies in the imaginary part of the ac susceptibility accompanied with two splitting of ZFC and FC curves occur in Fe³⁺ -doped α -Ga₂O₃. This behavior is suggested to be because the successive transition of two spin glasses arises from the magnetic anisotropy.