Quantum nonlocality usually refers to correlations that cannot be explained by any local hidden variable theory and it has been widely studied through Bell’ s inequalities.^{[1– 8]} Traditionally, it is believed that nonlocality can only be proven by quantum entanglement, which plays a vital role in quantum information processing and the violation of Bell’ s inequalities.^{[9– 11]} However, it is demonstrated by many works that nonlocality can exist without entanglement. For example, there exist sets of locally indistinguishable orthogonal pure product states that show nonlocality without entanglement.^[12] Measurement-induced nonlocality (MIN) was recently proposed by Luo and Fu, and is understood as some kind of correlation that is more general than nonlocality related to entanglement or violation of Bell’ s inequalities.^[8]

The MIN quantifies the nonlocal correlation in bipartite states from a geometric perspective. It considers the distance between the original state and the local measurement-induced state, preserving the local density matrix.^[8] Since the proposal of MIN, many researchers have studied this further. Sen et al. investigated the monogamy relation of MIN in some three and four-qubit states.^[11] Xu and Tong analyzed the dynamics of MIN.^[13] Hu and Fan proposed the entropic MIN.^[14] Xi et al. quantify the measurement-induced nonlocality from the perspective of the relative entropy.^[15] Moreover, some works have been devoted to comparing the MIN with other quantum correlations, ^{[16– 24]} such as geometric measure of discord, ^{[25, 26]} quantum discord, ^{[27, 28]} and measurement-induced disturbance.^[29] As a new correlation measure, a deep investigation about MIN is very desirable.

In this paper we study the MIN in n-qubit (n ≥ 3) W and Greenberger– Horne– Zeilinger (GHZ) superposition states, which will be called W– GHZ states hereafter. We find that the three-qubit W– GHZ states and the other ones (n ≥ 4) have different characteristics, especially the monogamy relation about MIN. Although all two-qubit reduced states of n-qubit W– GHZ states depend on the relative phases between the W and GHZ components, we find that the MIN depends on the relative phases only for the case of n= 3, i.e., the MIN for n ≥ 4 does not depend on the relative phases. Furthermore, we find that the monogamy relation of MIN is satisfied in all of the three-qubit W– GHZ states but it is not satisfied in many states for n ≥ 4. In addition, we also find that the monogamy equality of MIN holds in n-qubit W state for any n ≥ 3. This paper is organized as follows. In Section 2, we review some basic properties of MIN and monogamy. In Section 3, we analyze the MIN in three-qubit W– GHZ states. Furthermore, we study the MIN in n-qubit (n ≥ 4) W– GHZ states in Section 4. Finally, we give a brief conclusion.

The MIN of a bipartite quantum state ρ shared by two particles a and b is defined as^[8]

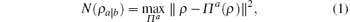
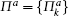
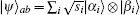
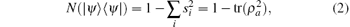
where the maximum is taken over all the local von Neumann measurements which does not disturb ρ ^a locally, satisfying , and ∥ X∥ ² = tr(X^† X) is taken to be Hilbert– Schmidt norm. In the following, when we consider the MIN in the state ρ _{abcd· · ·} we regard bcd· · · as a group and use the notation N(ρ _{a| bcd· · ·} ), and the local measurement is done on particle a. For bipartite pure states with the Schmidt decomposition , the MIN can be evaluated by^[8]

where ρ _a = tr_b(| ψ ⟩ 〈 ψ | ).

In the generalized Bloch representation, a two-qubit mixed state can always be written as

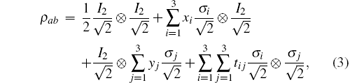
where I₂ is the identity operator for single qubits and {σ _i: i = 1, 2, 3} are three Pauli operators. It can be verified that

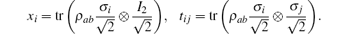
In this case, the MIN can be calculated as follows:^[8]

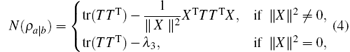
where T^T is the transpose of matrix T = (t_ij), λ ₃ is the minimum eigenvalue of the matrix TT^T, and 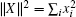with X = (x₁, x₂, x₃)^T.

In many-body quantum systems, monogamy is one of the most important properties, and several studies have been done on monogamy.^{[30– 33]} A correlation measure M satisfies the monogamy relation in n-particle state ρ if the relation

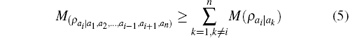
holds for all i = 1, 2, … , n. This relation means that the correlation between the particle i and the rest is not less than the sum of the correlations between two particles i and k.

In this section, we analyze the MIN in a three-qubit W– GHZ state

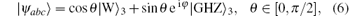
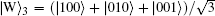
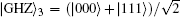
where and .

We first express the two-qubit reduced state ρ _ab = tr_c(| ψ _abc〉〈 ψ _abc| ) as the Bloch form shown in Eq. (3). The parameters x_i can be calculated by the equation

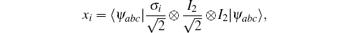
and there are

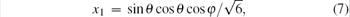
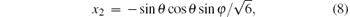
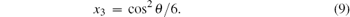
Since the state ρ _ab is a symmetric state, there is t_ij = t_ji and T^T = T. The elements of correlation matrix T are

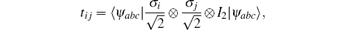
and we have

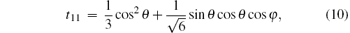
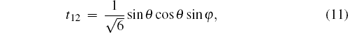
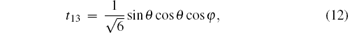
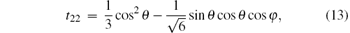
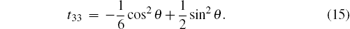
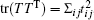
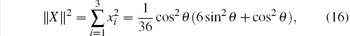
Now, we analyze the MIN N(ρ _{a| b}). Because , we find that for any parameter θ and φ there is tr(TT^T) = 1/4. Note that

we have the following discussion.

1) When cos θ = 0, there is ∥ X∥ ² = 0 and we should use the second line of Eq. (4) to calculate N(ρ _{a| b}). Simple calculation shows λ ₃ = 0, and there is N(ρ _{a| b}) = tr(TT^T)– λ ₃ = 1/4.

2) When cos θ ≠ 0, there is ∥ X∥ ² ≠ 0 and we should use the first line of Eq. (4) to calculate N(ρ _{a| b}). From the expression X^TTT^TX = ∥ T^TX∥ ², we obtain

leading to

We note that the above expression is also applicable when cos θ = 0.

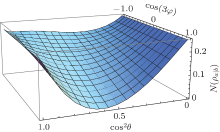
It is obvious that N(ρ _{a| b}) depends on the relative phase φ , which may not be surprising since ρ _ab depends on the parameter φ . However in the next section we will show that N(ρ _{a| b}) does not depend on φ in the n-qubit (n ≥ 4) W– GHZ state. Note that sin³θ cos ³θ ≥ 0, from Eq. (18) it can be observed that for any fixed θ not equal to 0 or π /2, N(ρ _{a| b}) will increase as cos (3φ ) decreases. Figure 1 shows how N(ρ _{a| b}) varies as a function of cos ²θ and cos (3φ ). It can be found that N(ρ _{a| b}) gets its maximal value 1/4 when cos θ = 0, and N(ρ _{a| b}) gets its minimal value 0 when cos (3φ ) = 1 and cos ²θ = 3/5.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. N(ρ a| b) of the two-qubit reduced state of the three-qubit W– GHZ state varies as a function of cos 2θ and cos (3φ ). For any fixed θ not equal to 0 or π /2, i.e., cos 2θ ≠ 0 or 1, N(ρ a| b) will increase as cos (3φ ) decreases.

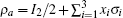
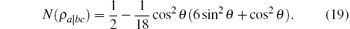
Next we analyze the monogamy property of MIN in the three-qubit W– GHZ state. Due to the symmetry, we only need to check whether Δ N = N(ρ _{a| bc})– N(ρ _{a| b})– N(ρ _{a| c}) ≥ 0 is satisfied. Since | ψ _abc⟩ is a pure state, N(ρ _{a| bc}) can be obtained from the reduced density matrix ρ _a according to Eq. (2). From the Bloch representation , and we obtain

Furthermore, due to N(ρ _{a| b}) = N(ρ _{a| c}), there is

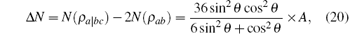
where

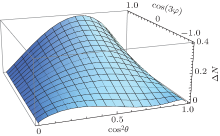
It is obvious that A ≥ 0 for any θ and φ , and therefore the monogamy relation is satisfied in all three-qubit W– GHZ states. It can be observed that for any fixed θ not equal to 0 or π /2, Δ N increases along the parameter cos (3φ ). Figure 2 shows that how Δ N varies as a function of cos ²θ and cos (3φ ). It is found that Δ N gets its maximal value 2/5 when cos (3φ ) = 1 and cos ²θ = 3/5, and Δ N gets its minimal value 0 when sin θ cos θ = 0 or in the state satisfying cos (3φ ) = − 1 and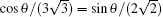

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Δ N = N(ρ a| bc)– 2N(ρ ab) varies as a function of cos 2θ and cos (3φ ). For any fixed θ not equal to 0 or π /2, i.e., cos 2θ ≠ 0 or 1, Δ N will increase as cos (3φ ) increases. There is Δ N ≥ 0 for any θ and φ that means the monogamy relation of MIN is always satisfied in the three-qubit W– GHZ state.

In this section, we investigate the MIN in the generalized n-qubit (n ≥ 4) W– GHZ state

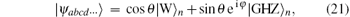
where θ ∈ [0, π /2], the W and GHZ states are and , respectively.

The discussion is parallel to three-qubit W– GHZ states. We first write the two-qubit reduced state ρ _ab in the Bloch form shown in Eq. (3). To obtain N(ρ _{a| b}), we need to calculate x_i and t_ij. After some derivation, we have

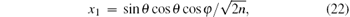
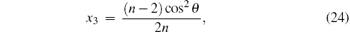
and the elements of the symmetric matrix T are

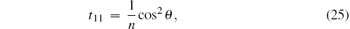
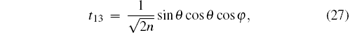
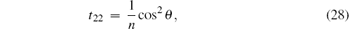
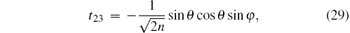
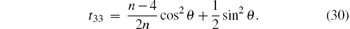
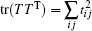
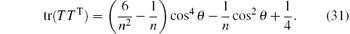
From the expression , we obtain

Note that

we have the following discussion.

1) When cos θ = 0, there is ∥ X∥ ² = 0 and we should use the second line of Eq. (4) to calculate N(ρ _{a| b}). Simple calculation shows λ ₃ = 0, and there is N(ρ _{a| b}) = tr(TT^T) – λ ₃ = 1/4.

2) When cos θ ≠ 0, there is ∥ X∥ ² ≠ 0 and we should use the first line of Eq. (4) to calculate N(ρ _{a| b}). From the expression X^TTT^TX = ∥ T^TX∥ ², it is found that

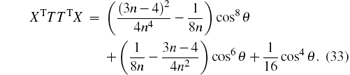
The MIN of ρ _ab is

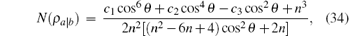
where c₁ = − n³ + 6n²− 32n + 16, c₂ = 3n³ + 16n, and c₃ = 3n³ + 2n². The above expression is also applicable for the case cos θ = 0.

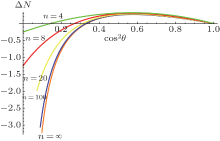
It is obvious that N(ρ _{a| b}) does not depend on the relative phase φ , which is a counterintuitive result since ρ _ab does depend on φ . Figure 3 shows how N(ρ _{a| b}) varies as a function of cos ²θ for the different value of n. It can be observed that for fixed θ not equal to π /2, N(ρ _{a| b}) will decrease along with n.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. N(ρ a| b) of the two-qubit reduced state of the n-qubit W– GHZ state varies as a function of cos 2θ , which does not vary with the relative phase φ although ρ ab depends on φ . For any fixed θ not equal to π /2, i.e., cos 2θ ≠ 0, N(ρ a| b) will decrease as n increases.

Next we analyze the monogamy property of the MIN in this generalized n-qubit W– GHZ state. We need to check whether Δ N = N(ρ _{a| bcd· · ·} )– (n– 1)N(ρ _{a| b}) ≥ 0 is satisfied. According to Eq. (2), the MIN N(ρ _{a| bcd· · ·} ) has the form

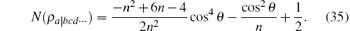
Therefore, there is

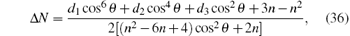
where d₁ = 5n– 6, d₂ = – 3n²– n + 8, and d₃ = 4n²– 7n– 2. When cos θ = 0, i.e., the state we consider is the n-qubit GHZ state, there is Δ N = (3– n)/4 < 0 and the monogamy relation is not satisfied. When cos θ = 1, i.e., the state we consider is the n-qubit W state, there is Δ N = 0 for any n, and the monogamy equality of MIN is satisfied. When cos θ ≠ 0 and n → ∞ , we have

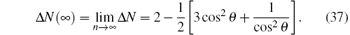
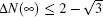
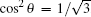
It can be derived that and the equality is achieved when . In addition, the quantity Δ N(∞ ) ≥ 0 when cos ²θ ∈ [1/3, 1]. Figure 4 shows how Δ N varies as a function of cos ²θ for different n. It can be observed that when cos ²θ ∈ [1/3, 1] there is Δ N ≥ 0 for any n, which means the monogamy of MIN is satisfied in these states.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Δ N = N(ρ a| bcd· · · )– (n– 1)N(ρ a| b) varies as a function of cos 2θ . When cos 2θ ∈ [1/3, 1] there is Δ N ≥ 0 for any n, which means the monogamy relation of MIN in these states is satisfied.

In this paper, we have explored the property of MIN in the superposition of n-qubit W and GHZ states. We provide three valuable results about this nonlocality measure: 1) The two-qubit reduced states of n-qubit W and GHZ superposition states depend on the relative phases for any n ≥ 3, but the MIN of the reduced two-qubit states do not depend on the relative phases for n ≥ 4; 2) The monogamy relation of MIN is satisfied in all three-qubit W and GHZ superposition states but it is not satisfied in all n-qubit (n ≥ 4) W and GHZ superposition states; 3) The monogamy equality of MIN is held in a n-qubit W state for any n ≥ 3.