In the past decades, the one-dimensional (1D) magnetic system, for example, the bimetallic compound AMn(S₂C₂O₂)₂(H₂O)₃· 4.5H₂O (A = Cu, Ni, Pd, Pt), has been one of the active fields in condensed matter. Many theoretical and experimental researchers have concentrated on the Haldane^[1] conjecture that the ground state of a half-odd integer spin chain is gapless and spin correlations decay in the power law, while the ground state of an integer spin chain is a gap and spin correlations decay exponentially. Then, a number of studies were concerned with the one-dimensional mixed spin chain with antiferromagnetic interaction.^{[2– 6]} The ground state of an isotropic mixed spin chain exhibits both ferromagnetic and antiferromagnetic elementary excitations. The excitation of the ferromagnetic aspect is gapless whereas the excitation of the antiferromagnetic aspect has a gap. Various methods have been developed to study the ground states and thermodynamic properties of the Heisenberg alternated spin chain. Pati^[7] studied the ground and excited states of uniform and dimerized alternating spin chain by using a density-matrix renormalization-group (DMRG) method and spin wave theory. Abolfath^[8] used a numerical exact diagonalization technique to study the phase diagram of one-dimensional quantum ferrimagnets. Sakai^[9] investigated the quantum magnetization plateaux of an anisotropic ferrimagnetic spin chain by using size-scaling analyses. Yamamoto^{[10, 11]} used the modified spin wave theory to investigate the thermodynamic properties of a Heisenberg ferrimagnetic spin chain and also studied the magnetic properties of quantum ferrimagnetic spin chains by the quantum Monte Carlo method. Langari^[12] used DMRG and exact diagonalization Lanczos methods to study the phase diagram of the XXZ ferrimagnetic chain in the presence of a transverse magnetic field. Chen^[13] applied self-consistent mean-field theory and the Green function method to research the ground states of a ferrimagnetic spin chain. In this paper, we study the excitation states and thermodynamic properties of an XXZ ferrimagnetic spin-(1/2, 1) chain with bond alternation by using the Schwinger-boson approach. This paper is organized as follows. In the second section, we present the Schwinger-boson approach to the anisotropy ferrimagnetic spin-(1/2, 1) chain with bond alternation. In the third section, we obtain the energy gaps, zero temperature free energy, and specific heat on the effect of bond alternation δ at Heisenberg point Δ = 1. In the fourth section, we discuss properties such as the energy spectrum, free energy, and specific heat based on the effect of the anisotropic parameter Δ . The conclusion and discussion are made in the final section.

The Hamiltonian of an XXZ ferrimagnetic spin-(1/2, 1) chain with bond alternation can be expressed as

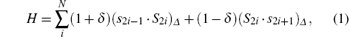
where s = 1/2 and S = 1 are the spin of sublattice A and sublattice B respectively, Δ is the XXZ anisotropic parameter, δ is the bonding alternation and (s · S)_Δ = s^xS^x + s^yS^y + Δ s^zS^z. The spin operator s_i can be represented by Schwinger bosons a_{i, ↑} and a_{i, ↓} :

The spin operator S_j can be represented by Schwinger bosons b_{j, ↑} and b_{j, ↓} :

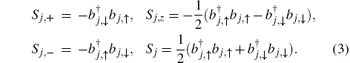
The Hamiltonian can be written as

where

and

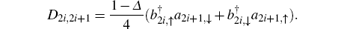
To implement the constraint or , we introduce two kinds of Lagrangian multiplier and . We make a mean field approximation on Eq. (4) and take the average value of the bond operator . In the momentum space, the Hamiltonian can be transformed into

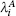
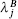
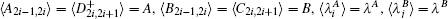
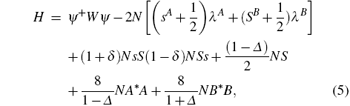
where

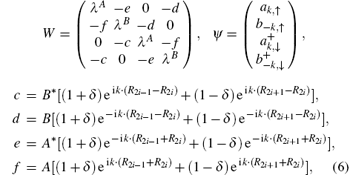
R_2i is the coordinate of S_2i. According to the diagonalization theory of Boson systems, the Heisenberg equation of motion can be written as

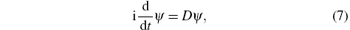
where

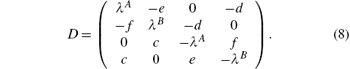
At Heisenberg point Δ = 1, the parameters are e = 0 and f = 0. The dynamic matrix can be rewritten as

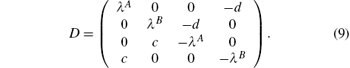
The energy spectrums can be obtained as

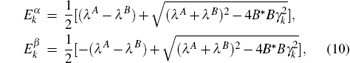
where and k is the wave vector. The free energy can be written as

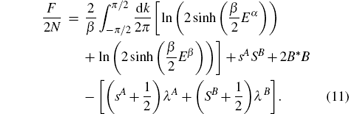
The mean-field self-consistent equations can be calculated by minimizing the free energy (i.e., δ F/δ B^* = 0, δ F/λ ^A = 0, δ F/λ ^B = 0). An infinitesimal external stagger magnetic field was supposed to be upward at site B and downward at site A at zero temperature. Due to the Bose– Einstein condensation, the mean-field self-consistent equations can be obtained as

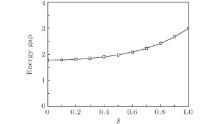
By solving the above equations numerically, the energy gap with different bond alternation δ at zero temperature are plotted as shown in Fig. 1. The energy gap is monotonically increased while δ is added from 0 to 1. The zero temperature free energy per unit cell is

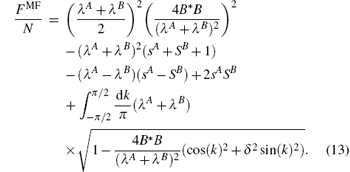
Due to the degree of freedom being overcounted by a factor of 2, as pointed out by Arovas and Auerbach, ^{[14, 15]} the free energy formula is calculated by dividing the part of fluctuation per unit cell F/N + 2s^AS^B by 2 and adding back the classic ground energy per cell − 2s^AS^B. The zero temperature free energy with different bond alternation δ as shown in Fig. 2. The free energy is monotonically decreased with the increase of δ . At finite temperature, the first equation of formula (12) can be modified as

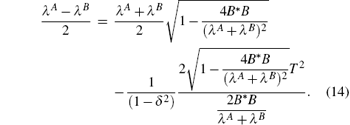
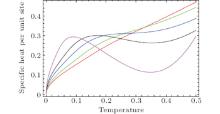
Wu^[16] pointed out that the SBMFT is not useful to describe the thermodynamic properties of the ferrimagnetic spin chain at intermediate and high temperatures. Thus, we discuss the thermodynamic properties of this model with T < 0.5. The specific heat with bond alternation versus temperature is calculated and plotted in Fig. 3. The effect of bond alternation δ on a specific heat is shown clearly at low temperature. The specific heat with a larger bond alternation parameter increases more rapidly and exhibits a peak when δ > 0.7 at lower temperature. The peak moves left while increasing the bond alternation δ . This means that the effect of bond alternation causes this abnormal phenomenon of specific heat at low temperature. When the ferrimagnetic spin chain with uniform bond alternation δ = 0, all the results mentioned above equal the results of Wu.^[16]

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The energy gap with different δ at zero temperature.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The free energy f0 with different δ at zero temperature.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The red, green, blue, black, and pink lines represent the specific heat of δ = 0, δ = 0.5, δ = 0.7, δ = 0.8, and δ = 0.9 respectively.

By using the eigenvalue equation Dψ = Eψ , we obtain the energy spectrum

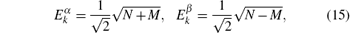
where

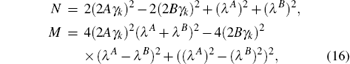
and . We only consider the effect of XXZ anisotropy Δ on the ferrimagnetic spin chain with uniform bond alternation δ = 0 in this section. The free energy can be written as

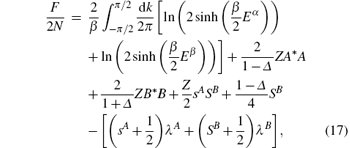
where Z is the number of nearest neighbor sites. The mean-field self-consistent equations can be obtained by minimizing the free energy (i.e., δ F/δ A^* = 0, δ F/δ B^* = 0, δ F/λ ^A = 0, δ F/λ ^B = 0). At zero temperature, the self-consistent equations are written as follows:

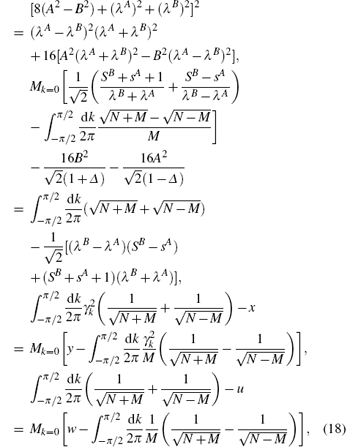
where

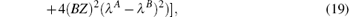
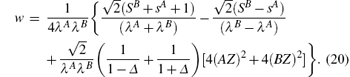
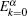
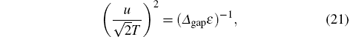
By solving the above self-consistent equations numerically, the excited energy spectrums with different anisotropic parameter Δ can be plotted respectively as shown in Fig. 4. The ferromagnetic branch increases more rapidly with smaller XXZ anisotropy from k = 0. The antiferromagnetic branch is lifted slowly while reducing the parameter Δ . Due to no boson condensation at low temperature, the first equation of formula (18) can be rewritten as

where

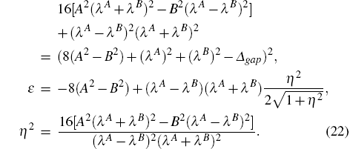
By solving the new self-consistent equations numerically, the energy gaps with different anisotropic parameter Δ versus temperature are plotted as Fig. 5. It can be seen from the figure that the free energy with smaller anisotropy is bigger at low temperature. The free energy curve with Δ = 1 decreases relative rapidly while that with smaller anisotropy, Δ < 1, descends little and slowly. The specific heat at low temperature is plotted in Fig. 6. It is found that the effect of XXZ anisotropy Δ is not obviously relative, compared with the effect of bond alternation δ . With increasing temperature, the curve with different anisotropy also increases with temperature. The specific heat with smaller anisotropy is reduced at the given temperature.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The solid, dotted, dashed, and dot– dashed lines represent the excited energy spectrum for Δ = 0.95, Δ = 0.9, Δ = 0.8, and Δ = 0.7 respectively.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The free energy versus T with different Δ .

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. The specific heat versus T with different Δ .

By using the Schwinger-boson mean-field theory, the XXZ ferrimagnetic spin-(1/2, 1) chain with bond alternation is explored. We present the energy gap, zero temperature free energy, and specific heat of an isotropic ferrimagnetic spin chain with bond alternation δ . Based on the effect of XXZ anisotropy Δ , the energy spectrums and thermodynamic properties at T < 0.4 are calculated respectively. The relation between the properties of a ferrimagnetic spin chain and XXZ anisotropy or bond alternation are shown clearly in the former figures.