In the past decades, there has been constant interest in quantum plasmas because of their possible applications to the next-generation intense laser– solid density plasma interaction, ^{[1– 3]} ultrasmall electronic devices, ^{[4, 5]} and superdense astrophysical systems, ^{[6, 7]} e.g. neutron stars, the interiors of white dwarfs, the cores of pre-supernova stars. In such a high-density plasma, due to the Pauli exclusion principle for fermions, quantum effects become prominent when the de Broglie thermal wavelength of particles is comparable to the inter-particle distance.

The effects of quantum static, quantum tunneling, and electron spin on linear and nonlinear collective behaviors in quantum plasmas have been well investigated by using the quantum hydrodynamic (QHD) equation.^{[8– 13]} Among them, one of the most important waves is the quantum ion acoustic wave (QIAW), which has applications to carbon nanotubes^{[14, 15]} and other laboratory and astrophysical settings. The small-amplitude QIAWs can be described by a Korteweg– de Vries (KdV) equation.^{[16, 17]} While for QIAWs with arbitrary large amplitudes, pseudopotential techniques can be used instead.^[18] The quantum diffraction effects have a large influence on the modulational instability of the QIAW packet on a small scale^[19] and the steepness of the double layer structure of QIAW.^[20] Monopolar, dipolar, and vortex street-type QIAWs can form separately in magnetized quantum plasmas, where the quantum diffraction effects strongly affect the length scales of the vortices.^[21]

The observation from the Advanced Satellite for Cosmology and Astrophysics has confirmed the existence of electron– positron-ion (EPI) plasmas.^[22] For dense EPI plasmas, quantum effects are also supposed to play an important role in governing the dynamics of charged particles.^{[23– 25]} In the linear limit, both acoustic waves and Langmuir waves can propagate in quantum EPI plasmas, where the increase of concentration of positrons can reduce the amplitude and width of the electrostatic solitons.^[26] The number density and temperature of positrons can significantly influence the collision between two QIAW solitary waves.^[27] The quantum acoustic double layer structure can exist in dense magnetized EPI plasmas, of which the steepness will increase as the magnetic field strength increases.^[28] The magnetosonic waves in magnetized degenerate EPI plasmas with spin effects were studied by considering the combined effects of quantum diffraction and spin magnetization energy, which shows that the effect of quantum corrections significantly modifies the dispersive properties of magnetosonic waves.^[29] The quantum freak waves in white dwarfs and magnetars can be investigated in ultrarelativistic degenerate EPI plasmas. The possible region for freak waves is defined precisely for typical parameters of white dwarfs and magnetars corona.^[30] Recently the arbitrary amplitude solitary and shock waves were also studied in unmagnetized quantum dusty EPI plasma, where the rarefactive solitons can exist in the presence of dust particles.^[31]

On the other hand, negative ions have been created successfully at the laboratory, ^[32] which makes it accessible to study the collective behavior in this plasma under controlled conditions. Negative ions can sometimes occur naturally by an electron attaching to neutral particles or can be injected from external sources in a lot of space and laboratory environments, such as the D region of the ionosphere, photosphere of the Sun, and plasma processing reactors. Akhter et al.^[33] studied Gardner solitons and double layers in a classical dusty electronegative plasma composed of positive and negative ions, cold electrons, hot electrons, and negatively charged static dust. The linear and nonlinear propagation of QIAWs have also been investigated in the quantum pair-ion plasmas.^{[34, 35]} Recently, the effects of negative ions on shock structures were also considered in a degenerate dissipative plasma, where the strength of shock wave increases with the decrease of negative ion density.^[36] The phase shifts in the head-on collision of quantum dust ion acoustic solitons are also affected by the ratio of positive ions number density to negative ions number density.^[37] It is found that shock wave structure is strongly dependent on electron density, quantum parameter, viscosity, and the ratio of positive to negative ions number density.^[38] Recently, the dressed QIAWs in an unmagnetized pair-ion plasma with weakly relativistic electron beams were studied by considering higher-order nonlinearity, which shows that the amplitudes and widths of the dressed solitons, of the KdV solitons, and of higher-order solutions all increase as the concentration of negative ions increases.^[39]

The core of a white dwarf has a high average bulk density which is typically ∼ 10³⁴ cm^{− 3}, ^[40] where the electrons are relativistically degenerate with weak electrostatic interaction while ions may be customarily classical or strongly coupled. In the outer mantle with a lower density (∼ 10²⁶ cm^{− 3}), the electron may be weakly relativistic-degenerate.^[41] The nonlinear solitary waves and shock waves were studied in relativistically degenerate electrons and positrons plasmas.^{[42– 45]} Accordingly in the present paper, we study the QIAWs in unmagnetized plasmas consisting of positive and negative ions as well as inertialess relativistically degenerate electrons and positrons. Here the ions are considered to be classical and inertial, while the electrons and positrons are treated as being inertialess, which will be considered as weakly relativistically degenerate plasma or an ultrarelativistic one. A nonlinear Schrö dinger equation (NLSE) is derived for QIAW, of which the modulation instability is considered. The results can be used to study the nonlinear collective processes in white dwarfs or magnetars.^{[46, 47]}

We consider a quantum plasma consisting of two polarity ions, and inertialess degenerated electrons and positrons. The charge neutrality at equilibrium reads n_{+ 0}+ n_p0 = n_e0+ n_{− 0}, where n_{+ 0}, n_{− 0}, n_p0, and n_e0 are the equilibrium number densities of positive ions, negative ions, positrons, and electrons, respectively. Collisions are neglected between electrons or positrons and the two types of ions. In our system, we are interested in the nonlinear propagation of one-dimensional (1D) low frequency (kV_{Ti, Tn} < ω < kV_Te, ω _pi) electrostatic waves with considering inertialess relativistically degenerate electrons, positrons, and inertial classical positive, negative ions. The set of equations describing the dynamics of positive ions and negative ions are given as

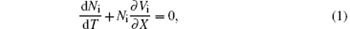
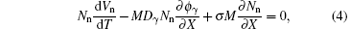
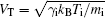
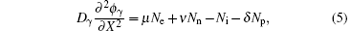
where N_i and N_n represent the number densities of positive ions and negative ions, normalized by their equilibrium number densities n_{+ 0} and n_{− 0}, respectively; V_i and V_n are the fluid velocities of the positive and negative ions, normalized by the ion thermal speed , with γ _i being the adiabatic index, k_B the Boltzmann constant, and T_i the temperature of positive ions. The σ = T_n/T_i and M = m_i/m_n are coefficients; D_γ is the dimensionless parameter and given as D_γ = T_Fe/_{γ i}T_i for γ = 5/3 and D_γ = β mc²/_{γ i}k_BT_i for γ = 4/3, referring to weakly relativistically degenerate and ultrarelativistic degenerate cases, respectively, with T_Fe = ħ ²(3π ²n_e0)^2/3/2mk_B being the Fermi temperature, β = λ _c (3π ²n_e0)^1/3 with λ _c = ħ /m_ec denoting the reduced Compton wavelength, and ħ being the Planck constant divided by 2π . In deriving the basic Eqs. (2) and (4), we consider the positive (negative) ion thermal pressure as P_i(n) = γ _ik_BT_i(n)n_i(n), where T_n is the temperature of negative ions. The normalized electrostatic potential ϕ _γ is defined as ϕ _γ = eϕ /k_BT_Fe and ϕ _γ = eϕ /β mc² for γ = 5/3 and γ = 4/3, respectively, where e is the elementary charge and ϕ is the electrostatic potential. The normalized electrostatic potential ϕ _γ is determined by

where μ = n_e0/n_i0, ν = n_n0/n_i0, and δ = n_p0/n_i0, which will satisfy the relationship μ + ν = 1 + δ due to the charge neutrality at equilibrium. In basic Eqs. (1)– (5), the space and time are normalized by ion Debye length and inverse ion plasma frequency , respectively. In this paper, we will consider both the weak relativistic degenerate plasmas and ultrarelativistic degenerate plasmas. Accordingly, we use the relativistic degenerate pressure as^[48]

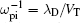
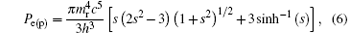
where m_r = m_e = m_p is the rest mass of electron or positron and c is the speed of light in a vacuum, h is the Planck constant, s = p_e(p)/m_rc, p_e(p) = (3h³n_e0(p0)/8π )^1/3 is the electron (positron) Fermi momentum, and n_e0(p0) represents the number density at equilibrium. Therefore, in the weakly relativistic limit s ≪ 1 and ultrarelativistic limit s ≫ 1, the expressions for degenerate pressure are as follows:

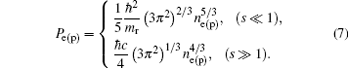
For inertialess electron and positron, we can obtain the expressions for electron and positron number densities as

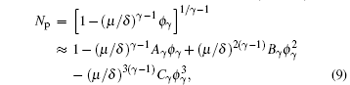
where the coefficients are A_γ = 1/(γ − 1), B_γ = (2 − γ )/2(γ − 1)²}, and C_γ = (2 − γ )(3 − 2γ )/6(γ − 1)³.

In order to investigate the modulational instability of the QIAW, we employ the standard reductive perturbation method to obtain an NLSE. We introduce the following stretched variables ξ and τ such that ξ = ε (X − λ T), τ = ε ²T, where ε is a small parameter measuring the strength of the nonlinearity and λ is the group velocity of the wave along the X direction. The dependent variables N_i, V_i, N_n, V_n, and ϕ _γ are expanded as

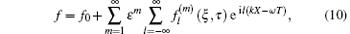
where f₀ = 1 for N_i and N_n, while f₀ = 0 for other variables; k and ω denote the wave number and frequency of the carrier wave, respectively. , and satisfy the reality condition . Substitute Eq. (10) into Eqs. (1)– (5) and equate different orders of ε , then a set of equations will be obtained. Meanwhile, we simplify ϕ _γ into ϕ unless otherwise stated. However, it is of significance to point out that the corresponding results are dependent on the value of γ .

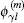
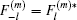
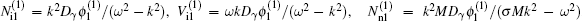
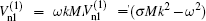
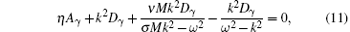
For the first order of ε with m = 1 and l = 1, we obtain , and and the dispersion relation

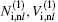
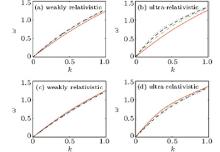
where the parameter is η = μ + μ ^{γ − 1}/δ ^{γ − 2}. For | l| ≠ 1 the , and are all set to be zero.

In order to investigate the effects of negative ions on behaviors of the wave modes, we plot ω versus k as shown in Fig. 1. Because we are interested in the QIAWs, so the part of high frequency is abandoned. In Figs. 1(a) and 1(b), we choose the parameters^{[39, 49]}ϕ ₀ = 0.01, K = 0.001, γ _i = 3, M = 16 (O⁺ and H⁻ ), ν = 0.6, γ = 5/3, n_i0 = 10²⁶ cm^{− 3}, n_p0 = 0.8 × 10²⁶ cm^{− 3}, T_i = 2.5 × 10⁵ K for the weakly relativistically degeneracy case and γ = 4/3, n_i0 = 10³⁴ cm^{− 3}, n_p0 = 0.8 × 10³⁴ cm^{− 3}, T_i = 1.5 × 10⁸ K for the ultrarelativistic degeneracy case with different negative ion temperatures normalized by the positive ion temperature: (a) σ = 1.0 (solid– red line), σ = 1.6 (dash– dotted green line), σ = 2.0 (dashed– black line), σ = 2.4 (dotted– blue line); (b) σ = 1.0 (solid– red line), σ = 2.0 (dash– dotted green line), σ = 3.0 (dashed– black line), and σ = 4.0 (dotted– blue line) respectively. Then the effects of the ratio of negative ion number density to positive ion number density on the dispersion relation are studied with σ = 1, (c) ν = 0.45 (solid– red line), ν = 0.55 (dash– dotted green line), ν = 0.65 (dashed– black line), ν = 0.75 (dotted– blue line); (d) ν = 0.15 (solid– red line), ν = 0.20 (dash– dotted green line), ν = 0.25 (dashed– black line), ν = 0.30 (dotted– blue line) for weakly relativistic and ultrarelativistic cases respectively, as shown in Figs. 1(c) and 1(d). The other parameters are the same as those in Figs. 1(a) and 1(b). From Fig. 1, it naturally follows that the frequencies of QIAW will go up with the increase of the temperature of negative ions in the weakly relativistic limit and the ultrarelativistic limit respectively. However, contrary to the effect of temperature, the rising of negative ions proportion will reduce the wave frequency. It is also clear from the figure that the changes of number density and temperature of negative ions will affect the QIAW modes more strongly in the ultrarelativistic limit than in the weakly relativistic case.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. The plots of the dispersion relation in the weakly relativistic case and ultrarelativistic case for different ratios of negative ion temperature to positive ion temperature: (a) σ = 1.0 (solid– red line), σ = 1.6 (dash– dotted green line), σ = 2.0 (dashed– black line), σ = 2.4 (dotted– blue line); (b) σ = 1.0 (solid– red line), σ = 2.0 (dash– dotted green line), σ = 3.0 (dashed– black line), σ = 4.0 (dotted– blue line) with ν = 0.6 and for different ratios of negative ion number density to positive ion number density: (c) ν = 0.45 (solid– red line), ν = 0.55 (dash– dotted green line), ν = 0.65 (dashed– black line), ν = 0.75 (dotted– blue line); (d) ν = 0.15 (solid– red line), ν = 0.20 (dash– dotted green line), ν = 0.25 (dashed– black line), and ν = 0.30 (dotted– blue line) with σ = 1.

For the second order of ε with m = 2 and l = 1, we obtain the expressions of , and as

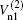
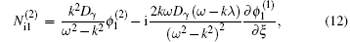
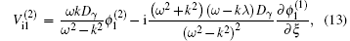
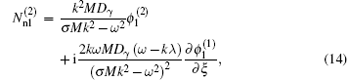
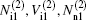
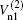
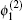
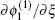
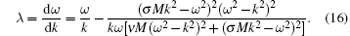
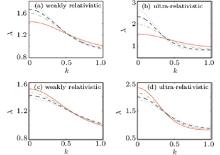
After eliminating , , a resulting equation is obtained, in which the coefficient of disappears by using the dispersion relation. Accordingly, the coefficient of is set to be zero to obtain the group velocity (i.e., compatibility condition) as

For simplicity, we visualize the plots of group velocity λ versus k with different temperatures and number densities of negative ions in Fig. 2. Parameters are the same as those in Fig. 1. We find that in both weakly relativisitic and ultrarelativistic limits, the modes with long wavelengths each have a greater group velocity than those with short wavelengths, which is different from the case studied by Misra and Shukla.^[40]

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. Plots of group velocity versus wave number in the weakly relativistic case and ultrarelativistic case for different ratios of negative ion temperature to positive ion temperature: (a) σ = 1.0 (solid– red line), σ = 1.6 (dash– dotted green line), σ = 2.0 (dashed– black line), σ = 2.4 (dotted– blue line); (b) σ = 1.0 (solid– red line), σ = 2.0 (dash– dotted green line), σ = 3.0 (dashed– black line), σ = 4.0 (dotted– blue line) with ν = 0.6 and for different ratios of negative ion number density to positive ion number density: (c) ν = 0.45 (solid– red line), ν = 0.55 (dash– dotted green line), ν = 0.65 (dashed– black line), ν = 0.75 (dotted– blue line); (d) ν = 0.15 (solid– red line), ν = 0.20 (dash– dotted green line), ν = 0.25 (dashed– black line), and ν = 0.30 (dotted– blue line) with σ = 1.

It is obvious from Figs. 2(a) and 2(b) that the higher temperature of negative ions makes a larger group velocity when the wave number is below a critical value k_c (e.g. for the weakly relativistic limit in Fig. 2(a)k_c ≈ 0.5). However, what should be mentioned above all is when the wave number k exceeds the critical value, the case reverses, i.e., a higher temperature of negative ions brings a lower group velocity. Meanwhile from Figs. 2(c) and 2(d), we can see that the number density of negative ions has the opposite effect on the group velocity compared with the temperature. Also, as in the influence on the dispersion relation, the changes of number density and temperature of negative ions will affect the group velocity more strongly in the ultrarelativistic limit than in the weakly relativistic one.

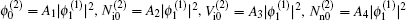
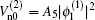
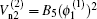
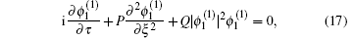
Then we consider the zero-harmonic mode for m = 2 and l = 0, and the results are , and , of which the coefficients are very tedious and then given in Appendix A. The components of l = 2 for the second order quantities are given as , and , of which the coefficients are also given in Appendix A. Ultimately substituting these expressions derived above into the third part of m = 3, l = 1, and with the help of the dispersion relation and the compatibility condition, we obtain the following NLSE

where the coefficients are

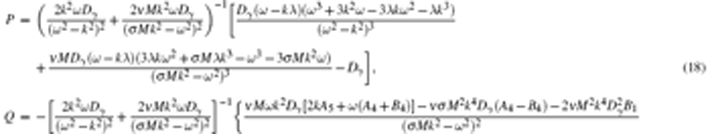
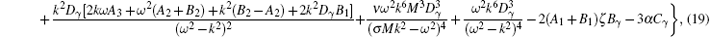
where we introduce new variables as ζ = μ − μ ^{2γ − 2}/δ ^{2γ − 3} and α = μ + μ ^{3γ − 3}/δ ^{3γ − 4}. It can be seen that the coefficients Q and P of the nonlinear and dispersive terms in NLSE (17) are all dependent on electron and positron relativistic degeneracy effects D_γ . Accordingly one can conveniently investigate the modulational instabilities of QIAWs, respectively, in weakly relativistic degeneracy and ultrarelativistic degeneracy by the small amplitude of NLSE (17).

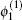
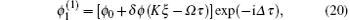
We will study the modulational instability of QIAWs in a four-component quantum plasma. We separate the amplitude into two parts as shown below

where ϕ ₀ is the constant amplitude of the pump carrier wave, δ ϕ ≪ ϕ ₀ is the small amplitude perturbation, the wave number K ≪ k, the frequency of the small amplitude modulation Ω ≪ ω , and Δ is the nonlinear frequency shift. Substituting Eq. (20) into Eq. (17) and putting terms of the same order together, we obtain the nonlinear frequency shift Δ = − Q| ϕ ₀| ² and

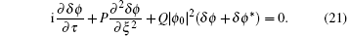
Letting δ ϕ = U + iV and assuming that U = U₀exp[i(Kξ − Ω τ )], V = V₀exp[i(Kξ − Ω τ )], we can obtain the following nonlinear dispersion relation for the small amplitude modulation of the QIAWs as

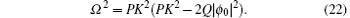
As one can see from the nonlinear dispersion relation, the small amplitude modulation will be unstable when the condition is satisfied. The corresponding local instability growth rate can be written as . The maximum modulational instability growth rate is Im(Ω )_max = | Q∥ ϕ ₀| ² for . It is interesting to note that the maximum instability growth rate equals the amount of the nonlinear frequency shift. For the cases of P < 0, Q > 0 or P > 0, Q < 0, it seems that Ω ² > 0 in each case indicating that the amplitude will be always stable to external perturbation. Specifically the wave propagates in the form of an envelope hole, which is called a dark soliton. Here we focus on the modulation instability case, which may help to explain the formation of the highly energetic waves in the universe. As one can see, the unstable region relies on the sign of PQ, which is in turn dependent on k and D_γ . As D_γ is a function of ν , the unstable region is determined by k and ν . In order to investigate the physical parameter space of the modulation instability, we give the stable and unstable regions in both weakly relativistic and ultrarelativistic limits on the ν – k plane. The modulational instability of QIAWs is investigated firstly for the weakly relativistic degeneracy case. The modulational instability regions in (ν , k) space are illustrated as the shadowed parts in Fig. 3 for different negative ion temperatures normalized by positive ion temperature: (a) σ = 1.0, (b) σ = 1.6, (c) σ = 2.0, and (d) σ = 2.4 where the corresponding parameters are the same as those in Fig. 1(a). For the ultrarelativistic degeneracy case, the modulational instability regions are also given in (ν , k) space as the shadowed parts in Fig. 4 for different negative ion temperatures normalized by positive ion temperature: (a) σ = 1.0, (b) σ = 2.0, (c) σ = 3.0, and (d) σ = 4.0 with the other parameters being the same as those in Fig. 1(b).

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Modulational instability regions (shadowed parts) in the weakly relativistic case with γ = 5/3 for different ratios of negative ion temperature to positive ion temperature: σ = 1.0 (a), 1.6 (b), 2.0 (c), and 2.4 (d) respectively.

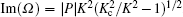
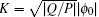
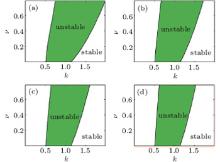
From Figs. 3 and 4 we can see that the proportion of negative ions has a predominant effect on the modulation instability. For a fixed k, values of ν cover a range in which the modulation instability occurs. The dimensionless parameter σ (the ratio of negative ion temperature to positive ion temperature) strongly changes the position and sizes of the stable and unstable regions. With the increase of σ , the modulational instability domains are diminished and shifted toward small wave numbers in both the weakly relativistic case and the ultrarelativistic case.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Modulational instability regions (shadowed parts) in the ultrarelativistic case with γ = 4/3 for different ratios of negative ion temperature to positive ion temperature: σ = 1.0 (a), 2.0 (b), 3.0 (c), and 4.0 (d).

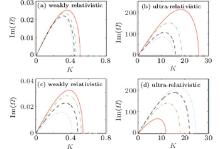
We also consider how the negative ion temperature and number density affect the modulational instability growth rate. We choose the parameters k = 0.8 and ν = 0.60 with different negative ion temperatures normalized by positive ion temperature: σ = 1.0 (solid– red line), σ = 1.6 (dash– dotted green line), σ = 2.0 (dashed– black line), σ = 2.4 (dotted– blue line) for the weakly relativistic case in Fig. 5(a); k = 0.5, ν = 0.35, σ = 1.0 (solid– red line), σ = 2.0 (dash– dotted green line), σ = 3.0 (dashed– black line), σ = 4.0 (dotted– blue line) for the ultrarelativistic case in Fig. 5(b). Subsequently in Figs. 5(c) and 5(d), we show the instability growth rates with different negative ion number densities for the weakly relativistic case and the ultrarelativistic case respectively. Parameters are adopted as k = 0.8, σ = 1, ν = 0.45 (solid– red line), ν = 0.55 (dash– dotted green line), ν = 0.65 (dashed– black line), ν = 0.75 (dotted– blue line) for the weakly relativistic case; k = 0.5, σ = 1, ν = 0.15 (solid– red line), ν = 0.20 (dash– dotted green line), ν = 0.25 (dashed– black line), ν = 0.30 (dotted– blue line) for the ultrarelativistic case. Other parameters in Fig. 5 are the same as those in Fig. 1. One can see from Figs. 5(a) and 5(b) that the increase of σ will reduce the growth rate both in the weakly relativistic limit and in the ultrarelativistic limit. We can also conclude that the increase of ν can reduce the instability growth rate in the weakly relativistic limit, except for the case indicated in Fig.5(d), which exhibits that the higher negative ion number density leads to a larger instability growth rate in the ultrarelativistic limit.

Fig. 5.

Figure Option ViewDownloadNew Window

Fig. 5. Modulational instability growth rates in the weakly relativistic case and the ultrarelativistic case for different ratios of negative ion temperature to positive ion temperature: (a) σ = 1.0 (solid– red line), σ = 1.6 (dash– dotted green line), σ = 2.0 (dashed– black line), and σ = 2.4 (dotted– blue line); (b) σ = 1.0 (solid– red line), σ = 2.0 (dash– dotted green line), σ = 3.0 (dashed– black line), and σ = 4.0 (dotted– blue line) with k = 0.8, ν = 0.6 and k = 0.5, ν = 0.35 respectively and for different ratios of negative ion number density to positive ion number density: (c) ν = 0.45 (solid– red line), ν = 0.55 (dash– dotted green line), ν = 0.65 (dashed– black line), ν = 0.75 (dotted– blue line); (d) ν = 0.15 (solid– red line), ν = 0.20 (dash– dotted green line), ν = 0.25 (dashed– black line), ν = 0.30 (dotted– blue line) with k = 0.8, σ = 1 and k = 0.5, σ = 1 respectively.

The maximum value of the instability growth rate and the corresponding critical modulation wave number are strongly affected by the relativistically degenerate parameter γ , the temperature ratio σ , and the proportion of negative ions ν . According to the maximum instability growth rate, there is a critical modulation wave number K_m with corresponding wave length λ _m = 2π /K_m. As can be seen, when the nonlinear modulation occurs, the envelope quantum ion acoustic solitary appears after a considerable time. The wave length of the solitary wave can be determined by the maximum growth rate of the instability. The critical wave number for the strongest instability will decrease with the increase of the negative ion temperature and number density for the weakly relativistic limit. For the ultrarelativistic limit, though the increase of negative ion temperature can lower the critical modulation wave number, the increase of negative ion number density will increase the critical modulation wave number.

The nonlinear propagation of QIAWs in dense quantum plasma composed of weak relativistic degenerate and ultrarelativistic degenerate electrons and positrons as well as warm classical positive and negative ions is investigated in the weak nonlinearity limit. We use the standard reductive perturbation technique to derive an NLSE for QIAWs. The latter can describe the characteristic of the envelope soliton wave with the nonlinear saturation occurring in a modulational instability region. The relativistically degenerate parameter and the ratio of negative ion density to positive ion density play significant roles in the modulational instability of QIAWs. With the increase of the temperature ratio σ , the modulational instability domains are diminished in both the weakly relativistic and the ultrarelativistic cases. The wave number of the strongest instability of the small amplitude modulation and the corresponding growth rate decrease with the increase of the negative ion temperature and number density in the weakly relativistic case. In the ultrarelativistic case, though the same situations will happen for different negative ion temperatures, they become different for different negative ion number densities. Meanwhile there is a critical modulation wave number above which the QIAWs will be stable. The results of our investigation will be meaningful in studying the nonlinear propagation and instability behaviors of low frequency QIAWs in astrophysical objects like white dwarfs. Finally, it is worth mentioning that the recently discovered strong coupling effect is attracting more and more attention. It is believed that a lot of useful results due to the strong coupling effect between the positive ions and negative ions are waiting to be discovered in the future.