Corresponding author. E-mail: shkli@bjtu.edu.cn
Project supported by the Fundamental Research Funds for the Central Universities of Ministry of Education of China (Grant No.2014JBM150).
In this paper, the robust output feedback cruise control for high-speed train movement with uncertain parameters is investigated. The dynamic of a high-speed train is modeled by a cascade of cars connected by flexible couplers, which is subject to rolling mechanical resistance, aerodynamic drag and wind gust. Based on Lyapunov’s stability theory, the sufficient condition for the existence of the robust output feedback cruise control law is given in terms of linear matrix inequalities (LMIs), under which the high-speed train tracks the desired speed, the relative spring displacement between the two neighboring cars is stable at the equilibrium state, and meanwhile a small prescribed H∞ disturbance attenuation level is guaranteed. One numerical example is given to illustrate the effectiveness of the proposed methods.
In recent years, high-speed railways are under construction in many countries to further enhance the efficiency of the railway traffic. High-speed trains operate at significantly faster speeds and are more eco-friendly than traditional railway traffic tools, in which the automatic train control (ATC) system is used to supervise, control and adjust the train operations to guarantee safety, punctuality and comfort.[1– 6]
In particular, one of the demanding control problems associated with the automatic train control (ATC) system is the cruise control problem that automatically controls the train speed to follow a desired trajectory. The proposed models for cruise control of the high-speed train can be classified into two categories. One is to model the whole train that consists of multiple cars as a single point mass.[7– 12] Moreover, by considering the interactive forces among the connected cars of the train, the other one is to construct the high-speed train model by a cascade of masses connected by flexible couplers, which provides more accuracy in characterizing the dynamics of the high-speed train.[13– 15]
In the most existing literature of the high-speed train, the resistance coefficients of trains were often assumed to be constant. However, when a train is traveling at high speed, the resistance coefficients will be changing with the operation conditions. So it is reasonable to regard the resistance coefficients of the train as time-varying. The robust adaptive tracking control method was derived for a multiple point mass high-speed train model with unknown and time varying resistance coefficients.[16] Besides, the adaptive backstepping control was developed for speed and position tracking of the high-speed train with uncertain resistive forces.[17] Moreover, by considering that the state measurements of the high-speed train are not completely available in reality, it is necessary to study the output feedback cruise control design for the high-speed train.[18] However, little literature can be found to deal with the robust output feedback cruise control problem for the high-speed train with uncertain parameters.
Motivated by the above discussion, in this paper, we will consider the multi-body model of the high-speed train with uncertain parameters, and design robust output feedback cruise control for the high-speed train. Different to the existing results, [16, 17] the resistance coefficients are assumed to be uncertain and varying within a range of values that are symmetric around the known nominal value. By considering the interactive forces among the connected cars of the trains, we present a new high-speed train with uncertain parameters and disturbances (such as wind gust and gradient resistance) modeled by a cascade of cars connected with flexible couplers. Based on Lyapunov’ s stability theory, a sufficient condition for the existence of the robust output feedback cruise control law is given in terms of linear matrix inequalities (LMIs), under which the high-speed train tracks the desired speed, the relative spring displacement between the two neighbored cars is stable at the equilibrium state (zero point), and meanwhile a smaller prescribed H∞ disturbance attenuation level is satisfied, which ensures the safety and comfort of the operation of the high-speed train. One numerical example is given to illustrate the effectiveness of the proposed methods.
The rest of this paper is organized as follows. In Section 2, the dynamic model of the high-speed train with uncertain parameters is presented. In Section 3, the robust output feedback cruise control of the high-speed train is designed. In Section 4, one numerical example is provided to demonstrate the effectiveness of the proposed methods. We conclude this paper in Section 5.
The force diagram of a high-speed train with n cars is plotted in Fig.1, which is modeled by a cascade of cars connected with flexible couplers, where the couplers play an important role in the connected cars and transmit traction/braking force in the longitudinal direction. The behavior function of the couplers is described by a spring model, for which the restoring force of the couplers is a function of the relative displacement ε between two adjacent cars as
 |
where k > 0 is the stiffness coefficient. When ε > 0, the spring will be stretched and the traction force for the train is generated. Otherwise, the spring will be compressed and the braking force for the train is generated.
The running high-speed train is subject to rolling mechanical resistance, aerodynamic drag and wind gust, which is given by the following Davis formula:[19]
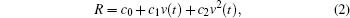 |
where v(t) is the velocity, c0, c1, c2 are resistance coefficients that can be obtained by a wind tunnel test, the first two terms represent the rolling mechanical resistance, and the third term is the aerodynamic drag. By considering that the resistance coefficients c0, c1, c2 of the high-speed train will change with operation conditions, we assume that the realized values of the coefficients c0, c1, c2 are given by 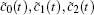
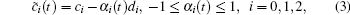 |
and the running resistance is obtained as
 |
Based on the above considerations, the dynamic equation of the high-speed train motion is given as follows:
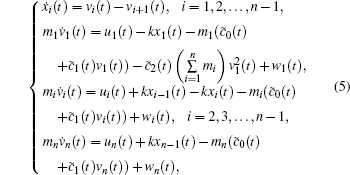 |
where xi(t) is the relative spring displacement between the two neighboring cars i and i + 1 at time t, vi(t) and ui(t) are the speed and control force of the i-th car respectively, mi is the i-th car’ s mass, wi(t), i = 1, 2, … , n represents the uncertain factors, such as wind gust, curve resistance and gradient resistance to the trains. To achieve the high-precise velocity tracking, we consider that each car of the high-speed train has its own driving force, and we will adopt the distributed driving design for each car of the high-speed train.
To study the cruise control problem of the high-speed train, the desired cruise speeds for each car of the high-speed train are denoted as ⊽ 1 = ⊽ 2 = … ⊽ n = vr, which are the equilibrium states of dynamic equation (5) and the relative spring displacements between adjacent cars are zero at the equilibrium state, i.e., 
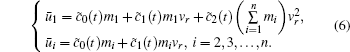 |
Let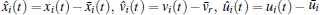
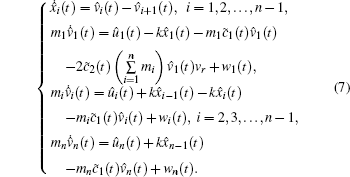 |
Furthermore, let 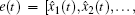
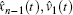

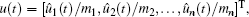
 |
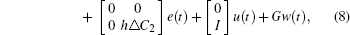
where

and I is an identity matrix with n dimensions.
Then the cruise control problem of the high-speed train is converted to the stability problem of the error dynamic equation (8) at zero.
To design the robust output feedback cruise control, the error dynamic equation (8) is rewritten as follows:
 |
where
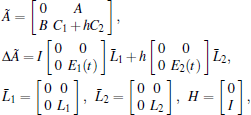
y(t) is the measured output, z(t) is the controlled output, D1 and D2 are the system parameters.
For the error dynamic equation (9), we consider a full-order dynamic output feedback controller with the following form:
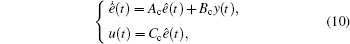 |
where ê (t)∈ R2n− 1 is the controller state. The matrices Ac, Bc, Cc are to be determined.
Let η (t)= [eT(t), ê T(t)]T. Applying the output feedback controller (10) to error dynamic equation, one can obtain the following closed-loop system
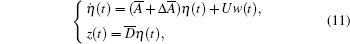 |
where

Then the robust output feedback cruise control for the high-speed train in this paper can be formulated as follows: for the closed-loop system (11), given a scalar γ > 0, find the dynamic output feedback controller (10) such that the following conditions are satisfied:
1) the closed-loop system (11) with w(t) = 0 is stable at zero;
2) under the zero initial condition, the controlled output z(t) satisfies
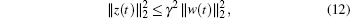 |
for any nonzero w(.)∈ L2[0, ∞ ) and all admissible uncertainties.
In this section, we will design the robust output feedback cruise control for the high-speed train. At first, based on the Lyapunov stability theory, the following theorem will provide a sufficient condition for the existence of the robust output feedback cruise control laws of the high-speed train.
Theorem 1 Consider the dynamic model of the high-speed train (Eq. (7)) with robust output feedback control (Eq. (10)). For a given constant γ , if there exist positive definite matrix P, matrices Ac, Bc, Cc such that the following matrix inequality holds:
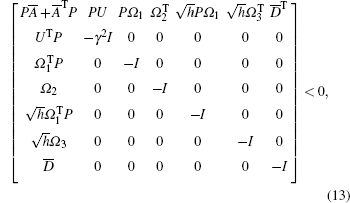 |
Where
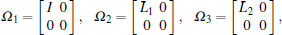
then the high-speed train under the robust output feedback control Eq. (10) tracks the desired speed, and the relative spring displacement between the two neighbored cars is stabilized to the equilibrium state, and meanwhile a disturbance attenuation level γ is guaranteed.
Proof At first, we will establish the stability condition for the closed-loop system (11) with w(t) = 0. For the closed-loop system (11) of the high-speed train with w(t) = 0, construct the following Lyapunov function candidate:
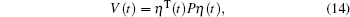 |
where P> 0.
By calculating the derivative of V(t) along the trajectory of the closed-loop system (11), one can obtain that
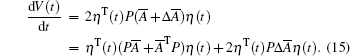 |
According to the Cauchy inequality that ATB + BTA ≤ ATA +BTB and matrices A and B with appropriate dimensions, together with the condition (3), it holds that
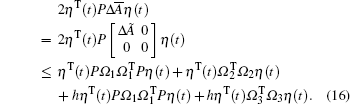 |
Then it can be derived from Eqs. (15)- (16) that
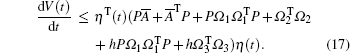 |
In addition, let Ф = P
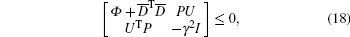 |
which, according to the Schur complement, implies that Ф < 0. Thus, we have dV(t)/dt < 0. Based on the Lyapunov stability theory, the closed-loop system (11) of the high-speed train is stable, i.e., under the robust output feedback control (10), each car of the high-speed train tracks the desired speed, and the relative spring displacement between the two neighboring cars is stabilized to the equilibrium state.
Next, for all nonzero w(.)∈ L2 [0, ∞ ), calculating the derivative of V(t) along the trajectory of the closed-loop system (11) yields that
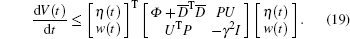 |
It obviously follows from Eqs. (18) and (19) that
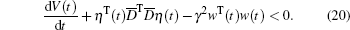 |
Thus, under the zero initial condition, integrating both sides of Eq. (20) from 0 to +∞ , and noting that V(+∞ ) = 0, we have
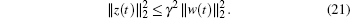 |
Then the closed-loop system (11) satisfies Eq. (12) for any nonzero w(.)∈ L2[0, +∞ ).
Therefore, the closed-loop system (11) is robustly stable with the H∞ disturbance attenuation level γ at the stationary states, i.e., the high-speed train tracks the desired speed, the relative spring displacement between the two neighboring cars is stable at the equilibrium state with a prescribed H∞ disturbance attenuation level. The proof is complete.
Note that condition (13) is not an LMI, and cannot be solved by the Matlab LMI Toolbox directly. In the sequel, a method of changing variables is applied to convert condition (13) to LMIs.
Partition P and its inverse as
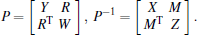
Let
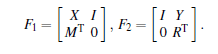
One has
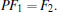
Define the new controller variables as
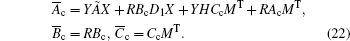 |
Therefore, the controller matrices Ac, Bc, Cc can be uniquely determined by
In the following, we will state our main results on the robust output feedback cruise control design of the high-speed train based on LMIs approach.
Theorem 2Consider the closed-loop system (11). Suppose that there exist positive definite matrices X, Y, and any matrices
 |
 |
where
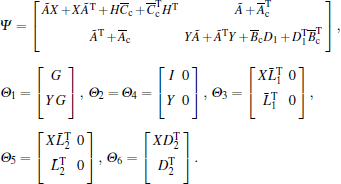
then the high-speed train tracks the desired speed, and the relative spring displacement between the two neighboring cars is stabilized to the equilibrium state, and meanwhile a disturbance attenuation level γ is guaranteed. Moreover, the controller parameters are given by
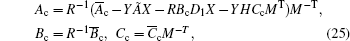 |
where R and M are any nonsingular matrices satisfying
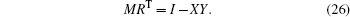 |
ProofBased on the change of controller variables (22), by pre and post-multiplying both sides of Eq. (13) by 
Remark 1 Theorem 2 provides a sufficient condition to design the robust cruise controller such that the high-speed train tracks the desired speed, the relative spring displacement between the two neighboring cars is stable at the equilibrium state with respect to the uncertain parameters and the external disturbances. For a given prescribed H∞ disturbance attenuation level γ > 0, the condition (23) in Theorem 2 takes the form of linear matrix inequalities, which can be solved in polynomial time and has a low computational complexity. Consequently, the proposed robust cruise controller can be better applied to the practical train cruise control and satisfies the real time requirement in reality.
In this section, a numerical example will be provided to illustrate the effectiveness of the proposed method for the robust output feedback cruise control of high-speed train movement. Consider a high-speed train is running with six cars, and the parameters of the high-speed train are given in Table 1, which are chosen from the the experimental results of the Japanese Shinkansen high speed train.[13] The uncertain parameters are assumed to be d0 = 0.58, d1 = 0.0026, d2 = 0.00009, and the time-varying parts α 0(t) = α 1(t) = α 2(t) = sin(t). The system parameters are given as D1 = 0.1I5 and D2 = 0.01I5.
| Table 1. Parameters of the high-speed train. |
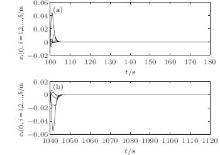
The speed command of the high-speed train is presented in Table 2, which shows that the high-speed train is running on a railway line with two cruise phases. Here, we mainly focus on the robust cruise control of the high-speed train in the cruise phases. In the first cruise phase [100 s, 1000 s], suppose that there are some uncertain disturbances (such as wind gust, gradient resistance) to the train operating at the beginning and the actual speed of each car of the high-speed train at t = 100 s is vi = 268km/h, i = 1, 2, … , 6, and the relative displacement between the two neighboring cars is xi = 0, i = 1, 2, … , 5, and in the second cruise phase [1040 s, 1600 s], when t = 1040 s, the instantaneous speeds of each car of the train are inspected as vi = 242km/h, i = 1, 2, … , 6 due to the uncertain disturbances and the relative displacement between the two neighboring cars is xi = 0, i = 1, 2, … , 5.
| Table 2. Speed command of the high-speed train. |
To achieve the cruise control for each car of the high-speed train, we apply the robust output feedback cruise control to each car of the high-speed train in the cruise phases [100 s, 1000 s] and [1040 s, 1600 s]. For a given smaller disturbance attenuationγ = 0.1, by solving the LMIs in Theorem 2 with the Matlab LMI toolbox, we can obtain the corresponding robust output feedback cruise controller. Under the robust output feedback cruise control, the speed curves for each car of the high-speed train in two cruise phases are plotted in Fig.2. From Fig.2, we can observe that each car of the high-speed train can quickly track the desired speed vr in the cruise phases. Additionally, the evolution curves of relative spring displacements between the two neighboring cars are depicted in Fig.3, which shows that the relative spring displacements between the two neighboring cars can be effectively kept at the equilibrium state (zero point) in a short time. Meanwhile, the deviations of relative spring displacements for each car of the high speed train from the equilibrium state are effectively controlled in the reasonable range of 0.06 m over the time, which ensures the safety and comfort of the operation of the high-speed train. The simulations show the effectiveness of the proposed method in this paper.
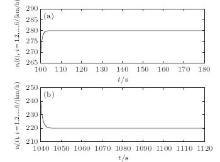 | Fig. 2. The speed curves of each car of the high-speed train in the cruise phases of [100 s, 180 s] (a) and [1040 s, 1120 s] (b). |
In this paper, we design the robust output feedback cruise control for high-speed train movement with uncertain parameters. By the Lyapunov stability theory, the sufficient condition for the existence of robust output feedback cruise controller is given in terms of linear matrix inequalities (LMIs), under which the high-speed train tracks the desired speed, the relative spring displacement between the two neighboring cars is stable at the equilibrium state with a smaller prescribed H∞ disturbance attenuation level, which ensures the safety and comfort of the operation of high-speed trains. One numerical example is given to illustrate the effectiveness of the proposed methods. Moreover, the robust output feedback cruise control for the high-speed train by considering the lateral force of wind gust will be the future research.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|