For a long time, the nature of light has been extensively studied by physicists. It has been a common sense that different optical fields may exhibit various properties of light. For instance, a coherent state of light is different from chaotic light, and the squeezed state of light displays some nonclassical properties, such as antibunching, squeezing, sub-Poisson statistics, etc. Thus, finding new optical fields provides us with a new opportunity to explore the nature of light. On the other hand, since most systems in the real world are immersed in a reservoir, studying optical fields' amplitude decay (dissipation in a lossy cavity) is related to quantum decoherence. A typical model for describing damping is displayed in the following master equation:^{[1– 4]}

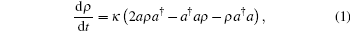where κ is the rate of decay, a^† and a are the photon creation operator and the annihilation operator respectively, and [a, a^† ] = 1. In this damping channel, a coherent field |α ⟩ ⟨ α | evolves into |α e ^{− κ t}⟩ , where |α ⟩ = D(α )|0⟩ , |0⟩ is the vacuum state, and D(α ) = exp [α a^† − α ^* a] is the displacing operator. It then naturally challenges us how does an initial displaced Fock state, whose density operator is D(α ) |m⟩ ⟨ m|D^† (α ) = ρ ₀, behave in the amplitude dissipative channel? Will a new optical field emerge in this decaying process? The displaced Fock state can be generated when a harmonic oscillator, initially in a Fock state controlled by an external source with the Hamiltonian being H = ω a^† a + fa^† + f^* a. In the following we will report that in the damping process the displaced Fock state will evolve into a new optical field whose density operator is

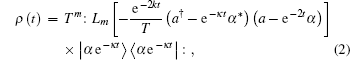where ∷ denotes normal ordering, T = 1 − e^{− 2kt}, and L_m is the m– th Laguerre polynomial, |α e^{− κ t}⟩ is a coherent state, |α e^{– κ t}⟩ = exp[− |α |²e^{− 2κ t} + α e^{– κ t}a^† ] |0⟩ . Equation (2) is the time evolution law of displaced Fock state in a dissipative channel.

This paper is arranged as follows. In Section 2 we briefly review how the master equation can be solved concisely by working in the thermo entangled state representation. In Sections 3 and 4, for examining how the displaced Fock state evolves in this channel, we use new generating function formulas and binomial formula involving two-variable Hermite polynomials to derive the normally ordered Laguerre polynomial weighted coherent state ρ (t), which is a mixed state. In Section 5 the average photon number in this new optical field is calculated, which not only explains the exponential damping of the displaced Fock state with time, but also shows that controlling the photon number can be realized by adjusting the value of m or |α |² or κ .

In order to directly solve Eq.(1), we take a convenient approach in which the thermo entangled state^{[5– 7]}

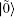
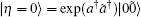
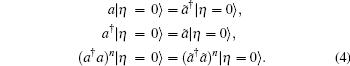is employed, where ã ^† is a fictitious mode accompanying the real photon mode a^† , is annihilated by ã , [ã , ã ^† ] = 1. The state obeys

Acting both sides of Eq.(1) on the state |η = 0⟩ ≡ |I⟩ , and denoting |ρ ⟩ = |I⟩ , we have

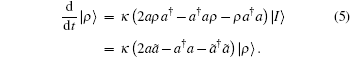In this way, the operator  (1) becomes a Schrö dinger equation of state vector |ρ ⟩ , and the formal solution of Eq.  (5) is

where |ρ ₀⟩ ≡ ρ ₀ |I⟩ , and ρ ₀ is the initial density operator which only includes real operators. Noting that the operators in Eq.  (6) obey the following commutative relation:

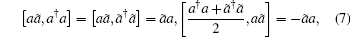and using the operator identity

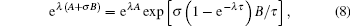which is valid for [A, B] = τ B, we have

where

Then substituting Eq.  (9) into Eq.  (6) and using Eq.  (4) yield

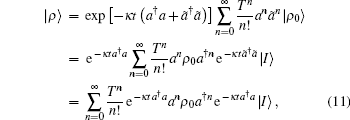which leads to the solution in operator-sum representation^[8]

Now using

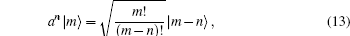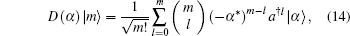and the operator identity

where H_{l, n} is the two-variable Hermite polynomial whose definition is given by^{[9– 11]}

or

we have

It then follows from e^{− kta† a} a^† e^{kta† a} = a^† e^{− kt} that

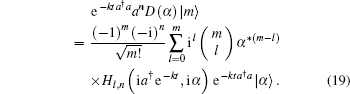Substituting Eq.  (19) into Eq.  (12) and using

as well as |0⟩ ⟨ 0| = : e^{− a† a}: , we have

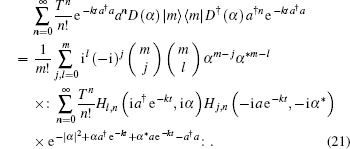Therefore, we need to derive some new summation formulas about Hermite polynomial H_{j, n} for further calculation.

Now we prove the following generating function formulas involving two-variable Hermite polynomials

In fact, using

after straightforward calculation, we have

Therefore,

RHS(21)

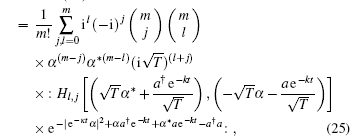then we still need a new binomial summation formula which involves H_{l, j}.

We propose the following new binomial summation formula involving H_{l, j}:

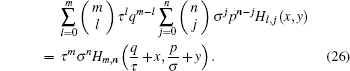Proof Noticing

where ∶ ∶ denotes anti-normal ordering within the symbol ∶ ∶ the operator a and a^† are permuted. Comparing the two sides of Eq.  (27) we obtain the antinormally ordered form of a^{† n}a^m

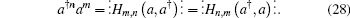Now using Eq.  (28) we consider

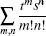
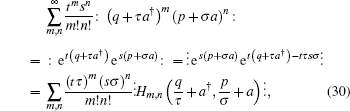Multiplying the two sides of Eq.  (29) by and making summation, its right-hand side becomes

so

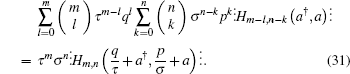This verifies the correctness of Eq.  (26), or we have

which is a new binomial theorem involving a two-variable Hermite polynomial. Then the summation in Eq.  (25) leads to

where in the last step we used

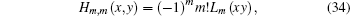and L_n(x) is the Laguerre polynomial

Equation   (33) represents a new optical field (a Laguerre-polynomial-weighted mixed state) generated as an output of the displaced Fock state in amplitude dissipative channel, so this damping process manifestly embodies quantum decoherence.

For this new density operator, we must check if Tr[ρ (t) = 1. In fact, using Eq.  (33) and the coherent state representation we have

where we have used the integration formula

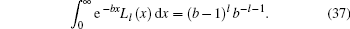Now we examine Eq.  (33) in two special cases. When m = 0, L_{m= 0}(x) = 1, so equation  (33) reduces to : |α e^{− κ t}⟩ ⟨ α e^{− κ t}| : = |α e^{− κ t}⟩ ⟨ α e^{− κ t}|, which represents the dissipation of an initial coherent state. On the other hand, when α = 0, from Eq.  (35) we obtain

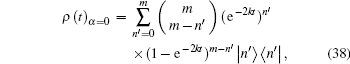which represents a binomial state. This explains that when the initial state is a number state |m⟩ ⟨ m|, it will evolve into a binomial state in the dissipative channel.

Then we evaluate the photon number expectation in the new optical field. Using Eqs.  (33) and (36) as well as the integration formula

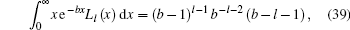we can obtain

which exhibits exponential damping with time. As many properties of a quantum optical field can be judged by photocounting, we can explore this new Laguerre-polynomial-weighted coherent state in this manner.

In summary, for the first time we have obtained a new optical field which is described by

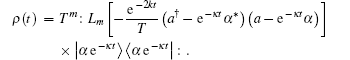
The time evolution law of displaced Fock state in a thermo reservoir is thus revealed. The photon number average in this field is , which shows that controlling the photon number can be implemented by adjusting the value of m or |α |² or κ .